i-manager Publications

i-manager's Journal on Mathematics (JMAT)

Current Issue Vol. 13 Issue 2

Mathematical Modeling of Higher Overtone Vibrational Frequencies in Dichlorine Monoxide
Some Types of Generalized Closed and Generalized Star Closed Sets in Topological Ordered Spaces
Optimizing Capsule Endoscopy Detection: A Deep Learning Approach with L-Softmax and Laplacian-SGD
Kernel Ideals in Semigroups
Modeling the Dynamics of Covid-19 with the Inclusion of Treatment, Vaccination and Natural Cure
Calculation of Combined Vibrational Frequencies in Cl₂O using Lie Algebraic Method

Most Cited

Volume 8 Issue 2 April - June 2019

Research Paper

In Series Connected RCL-Elements Loaded on Lossy Transmission Lines without the Heaviside’s Condition

Vasil G. Angelov*

*Department of Mathematics, University of Mining and Geology “St. I. Rilski”, Sofia, Bulgaria.

Angelov, G. V. (2019). In Series Connected RCL-Elements Loaded on Lossy Transmission Lines without the Heaviside’s Condition. i-manager's Journal on Mathematics, 8(2), 1-14. https://doi.org/10.26634/jmat.8.2.16649

Abstract

The main purpose of the present paper is to analyze the processes in a lossy transmission line terminated by in-series connected nonlinear RCL-loads. The distortion less propagation of the TEM-waves along the line under the Heaviside's condition has been investigated in a previous paper. Here we assume that the Heaviside condition is not satisfied. This leads to difficulties which can be overcome by a different type operator presentation of the mixed problem for the lossy transmission line. First, we formulate boundary conditions using the Kirchhoff's law, then transform the system in an operator form, and apply the fixed point method to obtain an existence-uniqueness theorem for a generalized solution. The uniqueness of solution is lost along the whole length of the line. Finally, we demonstrate the conditions of the main theorem on a typical example.

References

[1]. Angelov, V. G. (2013). A Method for Analysis of Transmission Lines Terminated by Nonlinear Loads. Nova Science Publishers, Incorporated.

[2]. Angelov, V. G. (2015). Josephson lossless transmission lines with nonlinear R-element. International Research Journal of Natural Sciences, 3(3), 59-79.

[3]. Angelov, V. G. (2016). Lossy Transmission Lines with Josephson Junction—Continuous Generalized Solutions. Communication in Applied Analysis, 20, 91-106.

[4]. Angelov, V. G., & Hristov, M. (2011). Distortionless lossy transmission lines terminated by in series connected RCL-loads. Circuits and Systems, 2(4), 297-310.

[5]. Chan, A. F. (2006). The Finite Difference Time Domain Method for Computational Electromagnetics. (Dissertation), University of Southern Queensland, Faculty of Engineering and Surveying.

[6]. Chua, L. O., & Lin, P. M. (1980). Machine Analysis of Electronic Circuits. Russian, Energy, Moscow.

[7]. Chua, L. O., Desoer, C. A., & Kuh, E. S. (1987). Linear and Nonlinear Circuits. McGraw-Hill Book Company, New York. https://doi.org/10.1002/bimj.4710300726

[8]. De Broglie, L. (1941). Problèmes de propagations guidées des ondes électromagnétiques (p. 6). Paris. https://doi.org/10.1090/S0002-9904-1952-09569-0

[9]. Dinakaran, C. (2015). Implementation of Shunt and Series FACTS Devices for Overhead Transmission Lines. International Electrical Engineering Journal (IEEJ), 6(8), 2009-2017.

[10]. Gaurav, Y., & Chauhan, R. K. (2016). Design of controllable dual-band bandpass filter using open loop triangular ring resonators loaded with stub coupled with transmission line. i-manager's Journal on Electronics Engineering, 7(2), 8-13. https://doi.org/10.26634/jele.7.2.11408.

[11]. Holt, C. A. (1963). Introduction to Electromagnetic Fields and Waves. John Wiley & Sons.

[12]. Jordan, E. C., & Balmain, K. G. (1968). Electromagnetic Waves and Radiating Systems, Second Edition. Prentice-Hall Inc.

[13]. Kalaga, S., & Yenumula, P. (2016). Design of Electrical Transmission Lines: Structures and Foundations. CRC Press.

[14]. Kapoor, G. (2019). Detection and classification of single line to ground boundary faults in a 138 kV six phase transmission line using Hilbert Huang transform. i-manager's Journal on Electrical Engineering, 12(3), 28-41. https://doi.org/10.26634/jee.12.3.15382.

[15]. Maas, S. A. (2003). Nonlinear Microwave and RF Circuits, 2^nd Ed., Artech House, Inc., Boston London.

[16]. Makwana, V. H., & Bhalja, B. R. (2016). Transmission Line Protection using Digital Technology, 1^st Ed. Springer.

[17]. Martin, F. (2015). Artificial Transmission Lines for RF and Microwave Applications. John Wiley & Sons. DOI:10.1002/9781119058403

[18]. Miamo, G., & Maffucci, A. (2001). Transmission Lines and Lumped Circuits: Fundamental and Applications, 2^nd Ed. Academic Press, New York.

[19]. Misra, D. K. (2004). Radio-frequency and Microwave Communication Circuits: Analysis and Design, 2^nd Ed. University of Wisconsin-Milwaukee. J. Wiley & Sons, Inc. DOI:10.1002/0471653764

[20]. Patil, N., & Behere, D. (2019). Performance analysis of PID and LQG control algorithms for antenna position control system. i-manager's Journal on Electrical Engineering, 13(1), 12-18. https://doi.org/10.26634/jee.13.1.16235

[21]. Raghuwanshi, S. K., Kumar, V., & Pandey, R. R. (2011). Guided and Leaky modes of a multilayer planar slab waveguide. i-manager's Journal on Electronics Engineering, 1(3), 14. https://doi.org/10.26634/jele.1.3.1421

[22]. Ramo, S., Whinnery, J. R., & Van Duzer, T. (1994). Fields and Waves in Communication Electronics. John Wiley & Sons.

[23]. Rosenstark, S. (1994). Transmission Lines in Computer Engineering. McGraw-Hill, Inc, New York, USA.

[24]. Ruikar, D. S. (2016). Electromagnetics and Transmission Lines. Nirali Prakashan.

[25]. Sharma, N., Sandhu, S., & Sharma, V. (2018). Analysis and Comparison of Rectangular Microstrip Patch Antennas with Omni-Directional Slotted Patch Antenna for Wireless Applications. i-manager's Journal on Communication Engineering and Systems, 7(2), 42-47. https://doi.org/10.26634/jcs.7.2.14105

[26]. Singh, R. (2013). Circuit Theory and Transmission Lines. McGraw Hill Education.

Full Article (HTML)

Pdf

Research Paper

Derivation of Johnson-Segalman Model in Cylindrical Co-ordinates

M. O. Mosa*

*Mathematics Teacher, Sudan International Grammar School, Sudan.

Mosa, M. O. (2019). Derivation Of Johnson-Segalman Model In Cylindrical Co-Ordinates. i-manager's Journal on Mathematics, 8(2), 15-24. https://doi.org/10.26634/jmat.8.2.16389

Abstract

The Johnson-Segalman model is a viscoelastic fluid model for non-affine deformations. However, non-Newtonian fluid is a fluid with properties that differ in any way from Newtonian fluids. The focus of this paper is deriving of Johnson-Segalman model in cylindrical co-ordinates (r, q, z). The continuity equation, momentum equation were derived from vector form to differential form. The Johnson-Segalman model was derived in cylindrical co-ordinates and system of partial differential equations were obtained.

References

[1]. Ahmed, N., Sharma, D., & Deka, H. (2012). MHD mixed convection and mass transfer from an infinite vertical porous plate with chemical reaction in presence of a heat source. Applied Mathematical Sciences, 6(21), 1011-1020.

[2]. Batchelor, G. K. (1967). An Introduction to Fluid Dynamics. Cambridge University Press, Cambridge.

[3]. Bird, R. B., Stewart, W. E., & Lightfoot, E. N. (2007). Transport Phenomena (Revised Second Ed.) John Wiley & Sons, New York.

[4]. Cowling, T. G. (1957). Magnetohydrodynamics. New York: Interscience Pub.

[5]. Hussanan, A., Ismail, Z., Khan, I., Hussein, A. G., & Shafie, S. (2014). Unsteady boundary layer MHD free convection flow in a porous medium with constant mass diffusion and Newtonian heating. The European Physical Journal Plus, 129(3), 46.

[6]. Ibrahim, K. A. Z. (2013). Analytical Solutions of Peristaltic Motion of Magnetohydrodynamic Non-newtonian Fluids (Doctoral Dissertation), Universiti Teknologi Malaysia.

[7]. Johnson Jr, M. W., & Segalman, D. (1977). A model for viscoelastic fluid behavior which allows non-affine deformation. Journal of Non-Newtonian fluid mechanics, 2(3), 255-270. https://doi.org/10.1016/0377-0257(77)80003-7

[8]. Kolkka, R. W., Malkus, D. S., Hansen, M. G., & Ierley, G. R. (1988). Spurt phenomena of the Johnson-Segalman fluid and related models. Journal of Non-Newtonian Fluid Mechanics, 29, 303-335. https://doi.org/10.1016/0377-0257(88)85059-6

[9]. Kundu, P. K., Cohen, I. M., & Dowling, D. R. (2008). Fluid Mechanics, (5^thEdi). Academic Press.

[10]. Mohyuddin, M. R., Hayat, T., Mahomed, F. M., Asghar, S., & Siddiqui, A. M. (2004). On solutions of some non-linear differential equations arising in Newtonian and non-Newtonian fluids. Nonlinear Dynamics, 35(3), 229-248.

[11]. Pedlosky, & Joseph (1987). Geophysical Fluid Dynamics. Springer.

[12]. Romig, M. F. (1964). The influence of electric and magnetic fields on heat transfer to electrically conducting fluids. In Advances in Heat Transfer (Vol. 1, pp. 267-354). Elsevier. https://doi.org/10.1016/S0065-2717(08)70100-X

[13]. Vasudev, C., Rao, U. R., Reddy, M. S., & Rao, G. P. (2010). Peristaltic pumping of Williamson fluid through a porous medium in a horizontal channel with heat transfer. American Journal of Scientific and Industrial Research, 1(3), 656-666.

[14]. Wang, Y., Ali, N., & Hayat, T. (2011). Peristaltic Motion of Magneto-hydrodynamic Generalized Second-order Fluid in a Symmetric Channel. Numerical method for partial differential equations. ARPN Journal of Engineering and Applied Sciences, 27(2), 415-435.

[15]. Widodo, B., Siswono, G. O., & Imron, C. (2015). Viscoelastic fluid flow with the presence of magnetic field past a porous circular cylinder. In Proceedings of 5^th ISERD International Conference. Bangkok, Thailand.

[16]. Zakaria, K. A., & Amin, N. S. (2014). The Lorentz Force. International Journal of Scientific and Innovative Mathematical Research (IJSIMR), 2(4), 378-380.

Full Article (HTML)

Pdf

Research Paper

Viral Microparasite Model with Distributed Delay

Appa Rao Dokala* , Kalesha Vali S., Paparao A. V.*

Department of Mathematics, Rajiv Gandhi University of Knowledge, IIIT Srikakulam, Andhra Pradesh, India.

Department of Basic Sciences and Humanities and Social Sciences, JNTUK University College of Engineering, Andhra Pradesh, India.

Department of Mathematics, JNTUK University College of Engineering, Andhra Pradesh, India.

Rao, D. A., Vali, K. S., and Paparao A. V. (2019). Viral Microparasite Model with Distributed delay. i-manager's Journal on Mathematics, 8(2), 25-34. https://doi.org/10.26634/jmat.8.2.16451

Abstract

In this paper, the authors analyze the stability analysis of directly transmitted viral microparasite model, which includes susceptible (x), infective (y), and immune (z) populations. The total population N is given by the sum of three populations (N=x + y +z). A distributed type of delay is incorporated in the interaction of susceptible (x) and infective (y) populations. The model is represented by the system of nonlinear integro-differential differential equations. It is observed that the model possessed a unique endemic equilibrium point and studied the system dynamics at this point using two delay kernels. The system is asymptotically stable if 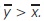. Numerical simulation is carried out using MATLAB with two delay kernels in support of stability analysis.

References

[1]. Anderson, R. M., & May, R. M. (1979). Population biology of infectious diseases: Part I. Nature, 280(5721), 361-367.

[2]. Anderson, R. M., & May, R. M. (1981). The population dynamics of microparasites and their invertebrate hosts. Philosophical Transactions of the Royal Society of London. B, Biological Sciences, 291(1054), 451-524. https://doi.org/10. 1098/rstb.1981.0005

[3]. Bailey, N. T. (1975). The Mathematical Theory of Infectious Diseases and its Applications. Charles Griffin & Company Ltd.

[4]. Brauer, F., Driessche, V. D. P., & Wu, J. (2008). Mathematical Epidemiology (pp. 3-17). Berlin: Springer.

[5]. Cooke, K. L. (1979). Stability analysis for a vector disease model. The Rocky Mountain Journal of Mathematics, 9(1), 31- 42.

[6]. Daley, D. J. & Gani, J. (1999). Epidemic Modeling: An Introduction. Cambridge University Press, Cambridge.

[7]. Evans, A. S. (1982). Viral Infections of Humans, 2^nd Ed. Plenum Medical Book Company, New York.

[8]. Frauenthal, J. G. (1980). Mathematical Modeling in Epidemiology. Springer Verlag, Berlin.

[9]. Hethcote, H. W. (1976). Qualitative analyses of communicable disease models. Mathematical Biosciences, 28(3-4), 335-356.

[10]. Karuna, B. N. R., Narayan, K. L., & Reddy, B. R. (2015). A mathematical study of an infectious disease model with time delay in CTL response. Global Journal of Pure and Applied Mathematics (GJPAM), 11.

[11]. Kuang, Y. (Ed.). (1993). Delay Differential Equations: With Applications in Population Dynamics (Vol. 191). Academic Press.

[12]. Kumar, R., Narayan, K. L., & Reddy, B. R. (2017). Mathematical Study of Epidemic Models (Doctor Dissertation, JNTU Hyderabad).

[13]. Murray, J. D. (2002). Mathematical Biology - I: An Introduction, 3^rd Edition. Springer Publication.

[14]. Nokes, D. J., & Swinton, J. (1995). The control of childhood viral infections by pulse vaccination. Mathematical Medicine and Biology, 12(1), 29-53.

[15]. Paparao, A., & Narayan, L. K. (2017). Dynamics of a prey predator and competitor model with time delay. International Journal of Ecology & Development, 32(1), 75-86.

[16]. Rao, A. D., Vali, K. S., & Paparao, A. (2017). Dynamics of directly transmitted viral microparasite model. International Journal of Ecology & Development, 32(4), 88-97.

[17]. Zhou, X., & Cui, J. (2011). Global stability of the viral dynamics with Crowley-Martin functional response. Bulletin of the Korean Mathematical Society, 48(3), 555-574.

Full Article (HTML)

Pdf

Research Paper

The Discrete Rising Sun Wrapped Cauchy Model

S. V. S. Girija* , P. Srinivasulu, Y. Sreekanth*, A.V. Dattatreya Rao****

,Department of Mathematics, Hindu College, Guntur, Andhra Pradesh, India.

Department of Statistics, Sri Chandra Reddy Degree College, Nellore, Andhra Pradesh, India.

**** Acharya Nagarjuna University, Guntur, Andhra Pradesh, India.

Girija, S. V. S., Srinivasulu, P., Sreekanth, Y., and Rao, A. V. D. (2019). The Discrete Rising Sun Wrapped Cauchy Model. i-manager's Journal on Mathematics, 8(2), 35-42. https://doi.org/10.26634/jmat.8.2.16634

Abstract

The circular models based on the Rising Sun function are motivated by purely mathematical considerations as a smoothing function and possible application. This work takes a further step in this direction using several mathematical tools such as Real Analysis along with MATLAB and is applied to enlarge the horizon of Mathematical Statistics. All the available circular / angular models are continuous distributions. Scant attention was made on construction and applications of discrete circular / angular models. Circular model using the Rising Sun function on continuous Wrapped Cauchy distribution is available in literature. Here an attempt is made to construct new discrete circular model by applying the methodology of discretization on the Rising Sun Wrapped Cauchy distribution and the population characteristics are evaluated using MATLAB.

References

[1]. Girija, S. V. S. (2010). Construction of New Circular Models. VDM Verlag, Germany.

[2]. Girija, S. V. S., Srihari, G. V. L. N., & Srinivas, R. (2019). On Discrete Wrapped Cauchy Model. IISTE-Journal of Mathematical Theory and Modeling, 9(4), 15-23. DOI: 10.7176/MTM.

[3]. Jammalamadaka, S. R., & Sengupta, A. (2001). Topics in Circular Statistics (Vol. 5). World Scientific.

[4]. Levy, P. (1939). L'addition des variables aléatoires définies sur une circonférence. Bulletin de la Société mathématique de France, 67, 1-41.

[5]. Mardia, K. V. (1975). Statistics of directional data. Journal of the Royal Statistical Society: Series B (Methodological), 37(3), 349-371. https://doi.org/10.1111/j.2517-6161.1975.tb01550.x

[6]. Mardia, K. V., & Jupp, P. E. (2000). Directional Statistics. John Wiley and sons.

[7]. McCullagh, P. (1996). Möbius transformation and Cauchy parameter estimation. The Annals of Statistics, 24(2), 787-808.

[8]. Radhika, A. J. V., Girija, S. V. S., & Rao, A. D. (2013). On rising Sun von mises and rising Sun wrapped Cauchy circular models. Journal of Applied Mathematics, Statistics and Informatics, 9(2), 41-55.

[9]. Rao, D. A. V., Sarma, R. I., & Girija, S. V. S. (2007). On wrapped version of some life testing models. Communications in Statistics—Theory and Methods, 36(11), 2027-2035. https://doi.org/10.1080/03610920601143832

[10]. Sarma, R. I., Rao, D. A. V., & Girija, S. V. S. (2009). On characteristic functions of wrapped half logistic and binormal distributions. International Journal of Statistics and Systems, 4(1), 33-45.

[11]. Sarma, R. I., Rao, D. A. V., & Girija, S. V. S. (2011). On characteristic functions of the wrapped lognormal and the wrapped Weibull distributions. Journal of Statistical Computation and Simulation, 81(5), 579-589. https://doi.org/10.1080/ 00949650903436547

[12]. Srihari, G. V. L. N., Girija, S. V. S., & Rao, D. A. V. (2018). On Discrete Wrapped Exponential distribution-Characteristics. International Journal of Scientific Research In Mathematical and Statistical Sciences, 5(2), 57-64.

[13]. Srinivas, R., Srihari, G. V. L. N., & Girija, S. V. S. (2018). On construction of Discrete Wrapped Lindley Distribution. i-manager's Journal on Mathematics, 7(4), 10. DOI:10.26634/jmat.7.4.15874

[14]. Van Rooij, V. A. C., & Schikhof, W. H. (1982). A Second Course on Real Functions. Cambridge University Press, Cambridge.

[15]. Wang, & Shimizu, K. (2014). Discrete Cardioid Distribution. Conference on Advances and Applications in Distribution Theory. The Institute of Statistical Mathematics, Tokyo, Japan.

[16]. Wintner, A. (1947). On the shape of the angular case of Cauchy's distribution curves. The Annals of Mathematical Statistics, 18(4), 589-593.

Full Article (HTML)

Pdf

Review Paper

Reliability Modelling and Analysis of Complex Industrial Systems - A Review

S. Z. Taj* , S. M. Rizwan**

*-** Department of Applied Mathematics & Science, College of Engineering, National University of Science & Technology, Sultanate of Oman.

Taj, S. Z., and Rizwan, S. M. (2019). Reliability Modelling and Analysis of Complex Industrial Systems - A Review. i-manager's Journal on Mathematics, 8(2), 43-60. https://doi.org/10.26634/jmat.8.2.16711

Abstract

This paper reviews the literature related to reliability modeling and analysis of complex industrial systems. The types of systems analyzed, various operating conditions and assumptions considered, different methodologies employed by the researchers, and the outcomes of the analysis, have been reviewed. The existing literature has been classified on the basis of significant system parameters. Behavior of important reliability indicators with respect to various system parameters has also been discussed. Tabular and graphical study is carried out to demonstrate crucial results. An up-to-date bibliography is presented systematically.

References

[1]. Adlakha, N., Taneja, G., & Batra, S. (2017). Reliability and cost-benefit analysis of a two-unit cold standby system used for communication through satellite with assembling and activation time. International Journal of Applied Engineering Research, 12(20), 9697-9702.

[2]. Ahmad, S., & Kumar, V. (2015). Profit analysis of a two-unit centrifuge system considering the halt state on occurrence of minor/major fault. International Journal of Advanced Research in Engineering and Applied Sciences, 4(4), 94-108.

[3]. Al Rahbi, Y., Rizwan, S. M., Alkali, B. M., Cowel, A., & Taneja, G. (2017a). Reliability analysis of a subsystem in aluminium industry plant. In 2017 6^th International Conference on Reliability, Infocom Technologies and Optimization (Trends and Future Directions) (ICRITO) (pp. 199-203). IEEE. https://doi.org/10.1109/ICRITO.2017.8342424

[4]. Al Rahbi, Y., Rizwan, S. M., Alkali, B. M., Cowell, A., & Taneja, G. (2017b). Reliability analysis of rodding anode plant in aluminium industry. International Journal of Applied Engineering Research, 12(16), 5616-5623.

[5]. Al Rahbi, Y., Rizwan, S. M., Alkali, B. M., Cowell, A., & Taneja, G. (2018a). Maintenance analysis of a butt thimble removal station in aluminum plant. International Journal of Mechanical Engineering and Technology, 9(4), 695-703.

[6]. Al Rahbi, Y., Rizwan, S. M., Alkali, B. M., Cowell, A., & Taneja, G. (2018b). Reliability analysis of rodding anode plant in an aluminum industry with multiple repairmen. Advances and Applications in Statistics, 53(5), 569-597.

[7]. Al Rahbi, Y., Rizwan, S. M., Alkali, B. M., Cowell, A., & Taneja, G. (2019a). Reliability analysis of a rodding anode plant in aluminum industry with multiple units failure and single repairman. International Journal of System Assurance Engineering and Management, 10(1), 97-109.

[8]. Al Rahbi, Y., Rizwan, S. M., Alkali, B. M., Cowell, A. & Taneja, G. (2019b). Reliability analysis of multiple units with multiple repairmen of rodding anode plant in aluminum industry. Advances and Applications in Statistics, 54(1), 151-178.

[9]. Ali, U. A., & Yusuf, I. (2014). Availability and profit analysis of a linear consecutive 2-out-of-4 repairable system with units exchange. American Journal of Applied Mathematics and Statistics, 2(2), 83-87. https://doi.org/10.12691/ajams-2-2-6

[10]. Babagana, M., Gimba, B., & Yusuf, I. (2016). Introducing probabilistic models for redundant system reliability. Operations Research and Decisions, 26(1), 5-18.

[11]. Barlow, R. E., & Proschan, F. (1965). Mathematical Theory of Reliability. New York: John Willey & Sons.

[12]. Bhardwaj, R. K., & Singh, R. (2016). Stochastic model of a cold-stand by system with waiting for arrival & treatment of server. American Journal of Operations Research, 6(4), 334-342. https://doi.org/10.4236/ajor.2016.64031

[13]. Bhardwaj, R. K., Kaur, K., & Malik, S. C. (2017). Reliability indices of a redundant system with standby failure and arbitrary distribution for repair and replacement times. International Journal of System Assurance Engineering and Management, 8(2), 423-431.

[14]. Bhatti, J., Chitkara, A. K., & Kakkar, M. (2013). Analysis of identical parallel system with failure followed by inspection policy using discrete distribution. International Journal of Scientific & Engineering Research, 4(5), 889-894.

[15]. Bhatti, J., Chitkara, A. K., & Kakkar, M. K. (2016). Stochastic analysis of dis-similar standby system with discrete failure, inspection and replacement policy. Demonstratio Mathematica, 49(2), 224-235. https://doi.org/10.1515/dema-2016- 0019

[16]. Davis, D. J. F. (1952). An analysis of some failure data. Journal of the American Statistical Association, 47(258), 113-150.

[17]. El-Damcese, M. A., & Shama, M. S. (2015). Reliability and availability analysis of a 2-state repairable system with two types of failure. Engineering Mathematics Letters.

[18]. El-Said, K. M., & El-Hamid, R. A. (2008). Comparison of reliability characteristics of two systems with preventive maintenance and different modes. Information and Management Sciences, 19(1), 107-118.

[19]. El-Said, K. M., & El-Sherbeny, M. S. (2005). Profit analysis of a two unit cold standby system with preventive maintenance and random change in units. Journal of Mathematics and Statistics, 1(1), 71-77.

[20]. El-Sherbeny, M. S., & Al-Hussaini, E. K. (2012). Characteristic reliability measures of mixed standby components and asymptomic estimation. International Journal of Statistics and Application, 2(3), 11-23. https://doi.org/10.5923/j.statistics. 20120203.01

[21]. Epstein, B., & Sobel, M. (1955). Sequential life tests in the exponential case. The Annals of Mathematical Statistics, 26(1), 82-93.

[22]. Fagge, N. J., Yusuf, I., & Ali, U. A. (2017). Availability evaluation of repairable system requiring two types of supporting device for operations. International Journal of Applied Mathematical Research, 6 (1), 14-19.

[23]. Gaver, D. P. (1963). Time to failure and availability of paralleled systems with repair. IEEE Transactions on Reliability, 12(2), 30-38. https://doi.org/10.1109/TR.1963.5218202

[24]. Goel, L. R., & Sharma, S. C. (1989). Stochastic analysis of a 2-unit standby system with two failure modes and slow switch. Microelectronics Reliability, 29(4), 493-498. https://doi.org/10.1016/0026-2714(89)90332-6

[25]. Goel, L. R., & Shrivastava, P. (1991). Profit analysis of a two-unit redundant system with provision for rest and correlated failures and repairs. Microelectronics Reliability, 31(5), 827-833. https://doi.org/10.1016/0026-2714(91)90019-4

[26]. Gopalan, M. N., & Bhanu, K. S. (1995). Cost analysis of a two unit repairable system subject to on-line preventive maintenance and/or repair. Microelectronics Reliability, 35(2), 251-258. https://doi.org/10.1016/0026-2714(95)90090-D

[27]. Gopalan, M. N., & Naidu, R. S. (1983). Busy-period analysis of a one-server two-unit system subject to non-negligible inspection time. Microelectronics Reliability, 23(3), 453-465. https://doi.org/10.1016/0026-2714(83)91172-1

[28]. Goyal, S., & Malhotra, R. (2017). A systematical study of reliability on various models. International Journal of Advance Research in Science and Engineering, 6(4), 864-876.

[29]. Gupta, R., & Bansal, S. (1991). Profit analysis of a two-unit priority standby system subject to degradation. International Journal of Systems Science, 22(1), 61-72. https://doi.org/10.1080/00207729108910589

[30]. Gupta, R., & Goel, R. (1991). Profit analysis of a two-unit cold standby system with abnormal weather condition. Microelectronics Reliability, 31(1), 1-5. https://doi.org/10.1016/0026-2714(91)90336-6

[31]. Gupta, R., Chaudhary, A., & Goel, R. (1993). Profit analysis of a two-unit priority standby system subject to degradation and random shocks. Microelectronics Reliability, 33(8), 1073-1079. https://doi.org/10.1016/0026-2714(93)90333-T

[32]. Gupta, S., & Gupta, S. K. (2013). Stochastic analysis of a reliability model of one-unit system with post inspection, post repair, preventive maintenance and replacement. International Journal of Mechanical Engineering and Robotics Research, 2(2), 178-188.

[33]. Haggag, M. Y. (2009). Cost analysis of a system involving common-cause failures and preventive maintenance. Journal of Mathematics and Statistics, 5(4), 305-310.

[34]. Haggag, M. Y. (2015). Profit analysis and availability of a repairable redundant 3-out-of-4 system involving preventive maintenance. International Journal of Scientific & Engineering Research, 6(8), 1161-1173.

[35]. Ibe, O. (2013). Markov Processes for Stochastic Modeling, 2^nd Edition. London: Elsevier.

[36]. Jiang, L., Feng, Q., & Coit, D. W. (2012). Reliability and maintenance modeling for dependent competing failure processes with shifting failure thresholds. IEEE Transactions on Reliability, 61(4), 932-948. https://doi.org/10.1109/ TR.2012.2221016

[37]. Kadyan, M. S. (2013). Reliability and profit analysis of a single-unit system with preventive maintenance subject to maximum operation time. Eksploatacjai Niezawodność, 15, 176-181.

[38]. Kakkar, M., Chitkara, A., & Bhatti, J. (2016). Reliability analysis of two dissimilar parallel unit repairable system with failure during preventive maintenance. Management Science Letters, 6(4), 285-296. https://doi.org/10.5267/j.msl.2016.2.001

[39]. Ke, J. C., & Wang, K. H. (2002). The reliability analysis of balking and reneging in a repairable system with warm standbys. Quality and Reliability Engineering International, 18(6), 467-478. https://doi.org/10.1002/qre.495

[40]. Keleş, B., Tekin, S., & Bakır, N. O. (2017). Maintenance policies for a deteriorating system subject to non-self-announcing failures. IEEE Transactions on Reliability, 66(1), 219-232. https://doi.org/10.1109/TR.2016.2639358

[41]. Kumar, A., & Agarwal, M. (1980). A review of standby redundant systems. IEEE Transactions on Reliability, 29(4), 290- 294. https://doi.org/10.1109/TR.1980.5220842

[42]. Kumar, A., & Saini, M. (2016). Analysis of a single-unit system with weibull failure and repair densities subject to server failure. Malaysian Journal of Science, 35(1), 15-22. https://doi.org/10.22452/mjs.vol35no1.3

[43]. Kumar, A., Baweja, S., & Barak, M. (2015). Stochastic behavior of a cold standby system with maximum repair time. Decision Science Letters, 4(4), 569-578. https://doi.org/10.5267/j.dsl.2015.5.002

[44]. Kumar, J., & Goel, M. (2016). Availability and profit analysis of a two-unit cold standby system for general distribution. Cogent Mathematics, 3(1). https://doi.org/10.1080/23311835.2016.1262937

[45]. Kumar, R., & Kapoor, S. (2013). Profit evaluation of a stochastic model on base transceiver system considering software based hardware failures and congestion of calls. IJAIEM, 2, 554-562.

[46]. Kuo, W., & Zuo, M. J. (2003). Optimal Reliability Modeling: Principles and Applications. John Wiley & Sons.

[47]. Li, W., Alfa, A. S., & Zhao, Y. Q. (1998). Stochastic analysis of a repairable system with three units and two repair facilities. Microelectronics Reliability, 38(4), 585-595. https://doi.org/10.1016/S0026-2714(97)00204-7

[48]. Mahmoud, M. A. W., Haggag, M. Y., & Elghany, A. A. (2017). Stochastic analysis of a duplicated standby system subject to shocks during repair. Journal of the Egyptian Mathematical Society, 25(2), 186-190. https://doi.org/10.1016/ j.joems.2017.01.003

[49]. Malhotra, R., & Taneja, G. (2013). Reliability and availability analysis of a single unit system with varying demand. Mathematical Journal of Interdisciplinary Sciences, 2(1), 77-88.

[50]. Malhotra, R., & Taneja, G. (2014). Stochastic analysis of a two-unit cold standby system wherein both units may become operative depending upon the demand. Journal of Quality and Reliability Engineering, https://doi.org/10. 1155/2014/896379

[51]. Malhotra, R., & Taneja, G. (2015a). Comparative analysis of two stochastic models subjected to inspection and scheduled maintenance. International Journal of Software Engineering and Its Applications, 9(10), 179-188. https://doi.org/10.14257/ijseia.2015.9.10.18

[52]. Malhotra, R., & Taneja, G. (2015b). Comparative study between a single unit system and a two-unit cold standby system with varying demand. SpringerPlus, 4(1), 705. https://doi.org/10.1186/s40064-015-1484-7

[53]. Martin, K. F. (1994). A review by discussion of condition monitoring and fault diagnosis in machine tools. International Journal of Machine Tools and Manufacture, 34(4), 527-551. https://doi.org/10.1016/0890-6955(94)90083-3

[54]. Mathew, A. G., Rizwan, S. M., Majumder, M. C., & Ramachandran, K. P. (2009). MTSF and availability of a two unit CC plant. In proceedings of the International Conference on Modeling, Simulation and Applied Optimization (pp. 1-5).

[55]. Mathew, A. G., Rizwan, S. M., Majumder, M. C., & Ramachandran, K. P. (2011). Reliability modelling and analysis of a two unit continuous casting plant. Journal of the Franklin Institute, 348(7), 1488-1505. https://doi.org/10.1016/j.jfranklin. 2010.04.016

[56]. Mathew, A. G., Rizwan, S. M., Majumder, M. C., Ramachandran, K. P., & Gulshan, T. (2009a). Optimization of a single unit CC plant with scheduled maintenance policy. In Proceedings of the International Conference on Recent Advances in Material Processing Technology (pp. 609-613).

[57]. Mathew, A. G., Rizwan, S. M., Majumder, M. C., Ramachandran, K. P., & Gulshan, T. (2009b). Profit evaluation of a single unit CC plant with scheduled maintenance. Caledonian Journal of Engineering, 5(1), 25-33.

[58]. Mathew, A. G., Rizwan, S. M., Majumder, M. C., Ramachandran, K. P., & Taneja, G. (2010a). Comparative analysis between profits of the two models of a CC plant. In AIP Conference Proceedings, 1298(1), 226-231. AIP. https://doi.org/10. 1063/1.3516306

[59]. Mathew, A. G., Rizwan, S. M., Majumder, M. C., Ramachandran, K. P., & Taneja, G. (2010b). Reliability modeling and analysis of a two-unit parallel CC plant with different installed capacities. Journal of Manufacturing Engineering, 5(3), 197- 204.

[60]. Mathew, A. G., Rizwan, S. M., Majumder, M. C., Ramachandran, K. P., & Taneja, G. (2011). Reliability analysis of identical two-unit parallel CC plant system operative with full installed capacity. International Journal of Performability Engineering, 7(2), 179-187. https://doi.org/10.23940/ijpe.11.2.p179.mag

[61]. Mortazavi, S. M., Karbasian, M., & Goli, S. (2017). Evaluating MTTF of 2-out-of-3 redundant systems with common cause failure and load share based on alpha factor and capacity flow models. International Journal of System Assurance Engineering and Management, 8(3), 542-552. https://doi.org/10.1007/s13198-016-0553-9

[62]. Munjal, A., & Singh, S. B. (2014). Reliability analysis of a complex repairable system composed of two 2-out-of-3: G subsystems connected in parallel. Journal of Reliability and Statistical Studies, 7, 89-111.

[63]. Murari, K., Goyal, V., & Rani, S. (1985). Cost analysis in two-unit warm standby models with a regular repairman and patience time. Microelectronics Reliability, 25(3), 473-483. https://doi.org/10.1016/0026-2714(85)90199-4

[64]. Naithani, A., Parashar, B., Bhatia, P. K., & Taneja, G. (2013). Cost benefit analysis of a 2-out-of-3 induced draft fans system with priority for operation to cold standby over working at reduced capacity. Advanced Modeling and Optimization, 15(2), 499-509.

[65]. Naithani, A., Parashar, B., Bhatia, P. K., & Taneja, G. (2017). Probabilistic analysis of a 3-unit induced draft fan system with one warm standby with priority to repair of the unit in working state. International Journal of System Assurance Engineering and Management, 8(2), 1383-1391. https://doi.org/10.1007/s13198-017-0608-6

[66]. Negi, S., & Singh, S. B. (2015). Reliability analysis of non-repairable complex system with weighted subsystems connected in series. Applied Mathematics and Computation, 262, 79-89. https://doi.org/10.1016/j.amc.2015.03.119

[67]. Nilsson, J., & Bertling, L. (2007). Maintenance management of wind power systems using condition monitoring systems-life cycle cost analysis for two case studies. IEEE Transactions on Energy Conversion, 22(1), 223-229. https://doi.org/10.1109/TEC.2006.889623

[68]. Niwas, R., Kadyan, M. S., & Kumar, J. (2016). MTSF (mean time to system failure) and profit analysis of a single-unit system with inspection for feasibility of repair beyond warranty. International Journal of System Assurance Engineering and Management, 7(1), 198-204. https://doi.org/10.1007/s13198-015-0362-6

[69]. Padmavathi, N., Rizwan, S. M., & Senguttuvan, A. (2015). Comparative analysis between the reliability models portraying two operating conditions of a desalination plant. International Journal of Core Engineering and Management, 1(12), 1-10.

[70]. Padmavathi, N., Rizwan, S. M., Pal, A., & Taneja, G. (2012). Reliability analysis of an evaporator of a desalination plant with online repair and emergency shutdowns. Aryabhatta Journal of Mathematics and Informatics, 4(1), 1-11.

[71]. Padmavathi, N., Rizwan, S. M., Pal, A., & Taneja, G. (2013a). Comparative analysis of the two models of an evaporator of a desalination plant. In Proc. of International Conference on Information and Mathematical Science (pp. 418-422).

[72]. Padmavathi, N., Rizwan, S., Pal, A., & Taneja, G. (2013b). Probabilistic analysis of an evaporator of a desalination plant with priority for repair over maintenance. International Journal of Scientific and Statistical Computing, 4(1), 1-8.

[73]. Padmavathi, N., Rizwan, S. M., Pal, A., & Taneja, G. (2014a). Probabilistic analysis of a desalination plant with major and minor failures and shutdown during winter season. International Journal of Scientific and Statistical Computing, 5(1), 15-23.

[74]. Padmavathi, N., Rizwan, S. M., Pal, A., & Taneja, G. (2014b). Probabilistic analysis of a seven unit desalination plant with minor/major failures and priority given to repair over maintenance. Arya Bhatta Journal of Mathematics and Informatics, 6(1), 219-230.

[75]. Parashar, B., & Bhardwaj, N. (2013). A comparative study of profit analysis of two reliability models on a 2-unit PLC system. International Journal of Scientific and Engineering Research, 4(4), 400-409.

[76]. Parashar, B., & Taneja, G. (2007). Reliability and profit evaluation of a PLC hot standby system based on a master-slave concept and two types of repair facilities. IEEE Transactions on Reliability, 56(3), 534-539. https://doi.org/10.1109/TR. 2007.903151

[77]. Pathak, V. K., Mehta, K., & Sahu, S. (2013). Performance analysis of a system having one main unit and two supporting units. International Journal of Mathematics and Computer Research, 1(07), 174-188.

[78]. Pathak, V., Mehta, K., Sahu, S., & Chaturvedi, R. (2013). Profit analysis of a system having one main unit and two supporting units. International Journal of Engineering and Computer Science, 2(10).

[79]. Rajamanickam, S. P., & Chandrasekar, B. (1997). Reliability measures for two-unit systems with a dependent structure for failure and repair times. Microelectronics Reliability, 37(5), 829-833. https://doi.org/10.1016/S0026-2714(96)00115-1

[80]. Ram, M., & Singh, S. B. (2012). Cost benefit analysis of a system under head-of-line repair approach using Gumbel- Hougaard family copula. Journal of Reliability and Statistical Studies, 5(2), 105-118.

[81]. Ram, M., Singh, S. B., & Singh, V. V. (2013). Stochastic analysis of a standby system with waiting repair strategy. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 43(3), 698-707. https://doi.org/10.1109/TSMCA.2012.2217320

[82]. Ramanarayanan, R., & Usha, K. (1979). n-unit warm standby system with Erlang failure and general repair and its dual. IEEE Transactions on Reliability, 28(2), 173-174. https://doi.org/10.1109/TR.1979.5220546

[83]. Rastogi, A. K., Kumar, A., & Goel, L. R. (1983). Effect of intermittent repair in a two unit redundant system with standby failure. Microelectronics Reliability, 23(6), 1051-1054. https://doi.org/10.1016/0026-2714(83)90519-X

[84]. Rizwan, S. M. (2007). Reliability analysis of a two unit system with two repairmen. Caledonian Journal of Engineering, 3(2), 1-5.

[85]. Rizwan, S., & Mathew, A. G. (2015). Performance analysis of port cranes. International Journal of Core Engineering and Management, 2(1), 133-140.

[86]. Rizwan, S. M., & Taneja, G. (2000). Profit analysis of a system with perfect repair at partial failure or complete failure. Pure and Applied Mathematika Sciences, 52(1/2), 7-14.

[87]. Rizwan, S. M., & Thanikal, J. V. (2014). Reliability analysis of a waste water treatment plant with inspection. Inspection' i-manager's Journal on Mathematics, 3(2), 21-26. https://doi.org/ 10.26634/jmat.3.2.3003

[88]. Rizwan, S. M., Chauhan, H., & Taneja, G. (2005). Stochastic analysis of systems with accident and inspection. Emirates Journal for Engineering Research, 10(2), 81-88.

[89]. Rizwan, S. M., Khurana, V., & Taneja, G. (2005). Reliability modeling of a hot standby PLC system. In Proceedings of the International Conference on Communication, Computer and Power (ICCCP'05) (pp. 486-489).

[90]. Rizwan, S. M., Khurana, V., & Taneja, G. (2007). Modelling and optimization of a single-unitplc system. International Journal of Modelling and Simulation, 27(4), 361-368. https://doi.org/10.1080/02286203.2007.11442438

[91]. Rizwan, S. M., Khurana, V., & Taneja, G. (2010). Reliability analysis of a hot standby industrial system. International Journal of Modelling and Simulation, 30(3), 315-322. https://doi.org/10.1080/02286203.2010.11442586

[92]. Rizwan, S. M., Padmavathi, N., & Taneja, G. (2015). Performance analysis of a desalination plant as a single unit with mandatory shutdown during winter. Aryabhatta Journal of Mathematics and Informatics, 7(1), 195-202.

[93]. Rizwan, V. M., Padmavathi, N., Pal, A., & Taneja, G. (2013). Reliability analysis of a seven unit desalination plant with shutdown during winter season and repair/maintenance on FCFS basis. International Journal of Performability Engineering, 9(5), 523-528.

[94]. Rizwan, S. M., Taneja, G., & Tuteja, R. K. (2000). Comparative study between the profits of two models for a two unit system with rest period of repairman. Journal of Decision and Mathematical Sciences, 5(1-3), 27-44.

[95]. Rizwan, S. M., Thanikal, J. V., & Torrijos, M. (2014). A general model for reliability analysis of a domestic wastewater treatment plant. International Journal of Condition Monitoring and Diagnostic Engineering Management, 17(3), 3-6.

[96]. Rizwan, S. M., Thanikal, J. V., Padmavathi, N., & Yazidi, H. (2015). Reliability & availability analysis of an anaerobic batch reactor treating fruit and vegetable waste. International Journal of Applied Engineering Research, 10(24), 44075-44079.

[97]. Sandler, G. (1963). System Reliability Engineering. Englewood Cliffs, NJ: Prentice-Hall.

[98]. Shakuntla, S., Lal, A. K., Bhatia, S. S., & Singh, J. (2011). Reliability analysis of polytube industry using supplementary variable technique. Applied Mathematics and Computation, 218(8), 3981-3992. https://doi.org/10.1016/j.amc.2011. 10.016

[99]. Sharma, U., & Kaur, J. (2016). Cost benefit analysis of a compressor standby system with preference of service, repair and replacement is given to recently failed unit. International Journal of Mathematics Trends and Technology, 30(2), 104- 108.

[100]. Sharma, U., & Sharma, G. (2016). Probabilistic analysis of a standby system with provision of concomitant working. International Journal of Engineering Trends and Technology, 40(1). 31-34.

[101]. Singh, N., Singh, D., & Saini, A. K. (2017). Cost-benefit analysis of two non-identical units cold standby system subject to heavy rain with partially operative after repair. Global Journal of Pure and Applied Mathematics, 13(2), 137-147.

[102]. Singh, R., & Dubey, G. K. (2013). Reliability and cost analysis of a standby redundant system with critical human errors. International Journal of Engineering and Mathematical Sciences, 4(1), 25-33.

[103]. Singh, V. V., & Ayagi, H. I. (2017). Study of reliability measures of system consisting of two subsystems in series configuration using copula. Palestine Journal of Mathematics, 6(2), 102-111.

[104]. Singh, V. V., Gulati, J., Rawal, D. K., & Goel, C. K. (2016). Performance analysis of complex system in series configuration under different failure and repair discipline using copula. International Journal of Reliability, Quality and Safety Engineering, 23(02), 1650010. https://doi.org/10.1142/S0218539316500108

[105]. Soni, K., Singh, U. R., & Jha, R. (2014). Mathematical analysis of reliability of M out of N warm standby system with repair facilities. International Journal of Advance Research and Innovation, 2(4), 744-749.

[106]. Srinivasan, S. K., & Gopalan, M. N. (1973). Probabilistic analysis of a two-unit system with a warm standby and a single repair facility. Operations Research, 21(3), 748-754. https://doi.org/10.1287/opre.21.3.748

[107]. Taj, S. Z., Rizwan, S. M., & Taneja, G. (2018). Reliability analysis of a wire drawing system with mandatory rest period. International Journal of Mechanical Engineering and Technology, 9(4), 1-10.

[108]. Taj, S. Z., Rizwan, S. M., Alkali, B. M., Harrison, D. K., & Taneja, G. (2017a). Probabilistic modeling and analysis of a cable plant subsystem with priority to repair over preventive maintenance. i-manager's Journal on Mathematics, 6(3),12- 21. https://doi.org/10.26634/jmat.6.3.13649

[109]. Taj, S. Z., Rizwan, S. M., Alkali, B. M., Harrison, D. K., & Taneja, G. L. (2017b). Reliability analysis of a single machine subsystem of a cable plant with six maintenance categories. International Journal of Applied Engineering Research, 12(8), 1752-1757.

[110]. Taj, S. Z., Rizwan, S. M., Alkali, B. M., Harrison, D. K., & Taneja, G. (2017c). Reliability modelling and analysis of a single machine subsystem of a cable plant. In 2017 7^th International Conference on Modeling, Simulation, and Applied Optimization (ICMSAO) (pp. 1-4). IEEE. https://doi.org/10.1109/ICMSAO.2017.7934917

[111]. Taj, S. Z., Rizwan, S. M., Alkali, B. M., Harrison, D. K., & Taneja, G. (2018a). Comparative analysis of reliability models of a cable plant portraying summer and winter operating strategy. In 9^th International Conference on Quality, Reliability, Infocom Technology and Business Operations. New Delhi, India: Springer.

[112]. Taj, S. Z., Rizwan, S. M., Alkali, B. M., Harrison, D. K.,& Taneja, G. (2018b). Performance analysis of a rod breakdown system. International Journal of Engineering and Technology, 7(4), 243-248.

[113]. Taj, S. Z., Rizwan, S. M., Alkali, B. M., Harrison, D. K., & Taneja, G. (2018c). Performance and cost benefit analysis of a cable plant with storage of surplus produce. International Journal of Mechanical Engineering and Technology, 9(8), 814-826.

[114]. Taj, S. Z., Rizwan, S. M., Alkali, B. M., Harrison, D. K., & Taneja, G. (2018d). Profit analysis of a cable manufacturing plant portraying the winter operating strategy. International Journal of Mechanical Engineering and Technology, 9(11), 370-381.

[115]. Taj, S. Z., Rizwan, S. M., Alkali, B. M., Harrison, D. K., & Taneja, G. (2018 e). Reliability analysis of a 3-unit subsystem of a cable plant. Advanced Application and Statistics, 52(6), 413-429. https://doi.org/10.17654/AS052060413

[116]. Taneja, G., & Malhotra, R. (2013). Cost-benefit analysis of a single unit system with scheduled maintenance and variation in demand. Journal of Mathematics and Statistics, 9(3), 155-160.

[117]. Taneja, G., Malhotra, R., & Chitkara, A. K. (2016). Comparative profit analysis of two reliability models with varying demand. Arya Bhatta Journal of Mathematicsand Informatics, 8(2), 305-314.

[118]. Taneja, G., Rizwan, S. M., & Kumar, R. (1992). Profit Analysis of a system with perfect repair at partial failure and priority for repair to complete failed unit. Pure and applied Mathematika Sciences, 35(1-2), 131-141.

[119]. Tuteja, R. K., & Taneja, G. (1992). Cost-benefit analysis of a two-server, two-unit, warm standby system with different types of failure. Microelectronics Reliability, 32(10), 1353-1359. https://doi.org/10.1016/0026-2714(92)90002-3

[120]. Tuteja, R. K., Rizwan, S. M., & Taneja, G. (1999). A two server system with regular repairman who is not always available. rd In 3 annual Conference of ISITA and National Symposium on Statistics - Applications to Trade & Industry (pp.231-237) Amritsar, Punjab, India.

[121]. Tuteja, R. K., Rizwan, S. M., & Taneja, G. (2000). Profit Evaluation of a two unit cold stand by system with tiredness and two types of repairman. Journal of Indian Society of Statistics and Operation Research, 21(1-4), 1-10.

[122]. Usha, K., & Ramanarayanan, R. (1980). Two n-Unit Cold-Standby Systems with an Erlang Distribution. IEEE Transactions on Reliability, 29(5), 434-435.

[123]. Wang, K. H., & Chiu, L. W. (2006). Cost benefit analysis of availability systems with warm standby units and imperfect coverage. Applied Mathematics and Computation, 172(2), 1239-1256. https://doi.org/10.1016/j.amc.2005.02.052

[124]. Wang, K. H., Ke, J. B., & Lee, W. C. (2007). Reliability and sensitivity analysis of a repairable system with warm standbys and R unreliable service stations. The International Journal of Advanced Manufacturing Technology, 31(11), 1223-1232.

[125]. Yamashiro, M. (1982). A repairable system with N failure modes and K standby units. Microelectronics Reliability, 22(1), 53-57. https://doi.org/10.1016/0026-2714(82)90050-6

[126]. Yearout, R. D., Reddy, P., & Grosh, D. L. (1986). Standby redundancy in reliability-a review. IEEE Transactions on Reliability, 35(3), 285-292. https://doi.org/10.1109/TR.1986.4335434

[127]. Yusuf, B., & Yusuf, I. (2013). Evaluation some reliability characteristics of a system under three types of failures with repair-replacement at failure. American Journal of Operational Research, 3(3), 83-91. DOI: 10.5923/j.ajor.20130303.02

[128]. Yusuf, I. (2016). Reliability modelling of a parallel system with a supporting device and two types of preventive maintenance. International Journal of Operational Research, 25(3), 269-287. [129]. Yusuf, I., & Bala, S. I. (2013). Modeling and evaluation of MTSF of a repairable 2-out-of-4 warm standby system attended by repair machines and repairmen. Engineering Mathematics Letters, 2(1), 81-89.

[130]. Yusuf, I., & Hussaini, N. (2012). Evaluation of reliability and availability characteristics of 2-out of-3 standby system under a perfect repair condition. American Journal of Mathematics and Statistics, 2(5), 114-119. https://doi.org/10.5923/ j.ajms.20120205.03

[131]. Yusuf, I., & Hussaini, N. (2014). A comparative analysis of three unit redundant systems with three types of failures. Arabian Journal for Science and Engineering, 39(4), 3337-3349.

[132]. Yusuf, I., & Koki, F. S. (2013). Assessment of profit of a two-stage deteriorating linear consecutive 2-out-of-3 repairable System. Journal of Applied Mathematics and Physics, 1(3), 21-27.https://doi.org/10.4236/jamp.2013.13005

[133]. Yusuf, I., Suleiman, K., Bashir, Y., & Ali, U. A. (2014). Stochastic modelling and analysis of a repairable 2-out-of-4 system. International Journal of Mathematics in Operational Research, 6(1), 23-34.

[134]. Zio, E. (2016). Some challenges and opportunities in reliability engineering. IEEE Transactions on Reliability, 65(4), 1769-1782. https://doi.org/10.1109/TR.2016.2591504

i-manager's Journal on Mathematics (JMAT)

Current Issue Vol. 13 Issue 2

Most Read

Most Cited

Volume 8 Issue 2 April - June 2019

In Series Connected RCL-Elements Loaded on Lossy Transmission Lines without the Heaviside’s Condition

Vasil G. Angelov*

*Department of Mathematics, University of Mining and Geology “St. I. Rilski”, Sofia, Bulgaria.

Angelov, G. V. (2019). In Series Connected RCL-Elements Loaded on Lossy Transmission Lines without the Heaviside’s Condition. i-manager's Journal on Mathematics, 8(2), 1-14. https://doi.org/10.26634/jmat.8.2.16649

Abstract

References

Full Article (HTML)

Pdf

Derivation of Johnson-Segalman Model in Cylindrical Co-ordinates

M. O. Mosa*

*Mathematics Teacher, Sudan International Grammar School, Sudan.

Mosa, M. O. (2019). Derivation Of Johnson-Segalman Model In Cylindrical Co-Ordinates. i-manager's Journal on Mathematics, 8(2), 15-24. https://doi.org/10.26634/jmat.8.2.16389

Abstract

References

Full Article (HTML)

Pdf

Viral Microparasite Model with Distributed Delay

Appa Rao Dokala* , Kalesha Vali S.**, Paparao A. V.***

Rao, D. A., Vali, K. S., and Paparao A. V. (2019). Viral Microparasite Model with Distributed delay. i-manager's Journal on Mathematics, 8(2), 25-34. https://doi.org/10.26634/jmat.8.2.16451

Abstract

References

Full Article (HTML)

Pdf

The Discrete Rising Sun Wrapped Cauchy Model

S. V. S. Girija* , P. Srinivasulu**, Y. Sreekanth***, A.V. Dattatreya Rao****

*,***Department of Mathematics, Hindu College, Guntur, Andhra Pradesh, India. ** Department of Statistics, Sri Chandra Reddy Degree College, Nellore, Andhra Pradesh, India. **** Acharya Nagarjuna University, Guntur, Andhra Pradesh, India.

Girija, S. V. S., Srinivasulu, P., Sreekanth, Y., and Rao, A. V. D. (2019). The Discrete Rising Sun Wrapped Cauchy Model. i-manager's Journal on Mathematics, 8(2), 35-42. https://doi.org/10.26634/jmat.8.2.16634

Abstract

References

Full Article (HTML)

Pdf

Reliability Modelling and Analysis of Complex Industrial Systems - A Review

S. Z. Taj* , S. M. Rizwan**

*-** Department of Applied Mathematics & Science, College of Engineering, National University of Science & Technology, Sultanate of Oman.

Taj, S. Z., and Rizwan, S. M. (2019). Reliability Modelling and Analysis of Complex Industrial Systems - A Review. i-manager's Journal on Mathematics, 8(2), 43-60. https://doi.org/10.26634/jmat.8.2.16711

Abstract

References

Full Article (HTML)

Pdf

Appa Rao Dokala* , Kalesha Vali S., Paparao A. V.*

S. V. S. Girija* , P. Srinivasulu, Y. Sreekanth*, A.V. Dattatreya Rao****

,Department of Mathematics, Hindu College, Guntur, Andhra Pradesh, India.

Department of Statistics, Sri Chandra Reddy Degree College, Nellore, Andhra Pradesh, India.

**** Acharya Nagarjuna University, Guntur, Andhra Pradesh, India.