References
[1]. Anderson, R. M., & May, R. M. (1979). Population biology of infectious diseases: Part I. Nature, 280(5721), 361-367.
[2]. Anderson, R. M., & May, R. M. (1981). The population dynamics of microparasites and their invertebrate hosts. Philosophical Transactions of the Royal Society of London. B, Biological Sciences, 291(1054), 451-524. https://doi.org/10. 1098/rstb.1981.0005
[3]. Bailey, N. T. (1975). The Mathematical Theory of Infectious Diseases and its Applications. Charles Griffin & Company Ltd.
[4]. Brauer, F., Driessche, V. D. P., & Wu, J. (2008). Mathematical Epidemiology (pp. 3-17). Berlin: Springer.
[5]. Cooke, K. L. (1979). Stability analysis for a vector disease model. The Rocky Mountain Journal of Mathematics, 9(1), 31- 42.
[6]. Daley, D. J. & Gani, J. (1999). Epidemic Modeling: An Introduction. Cambridge University Press, Cambridge.
[7]. Evans, A. S. (1982). Viral Infections of Humans, 2nd Ed. Plenum Medical Book Company, New York.
[8]. Frauenthal, J. G. (1980). Mathematical Modeling in Epidemiology. Springer Verlag, Berlin.
[9]. Hethcote, H. W. (1976). Qualitative analyses of communicable disease models. Mathematical Biosciences, 28(3-4), 335-356.
[10]. Karuna, B. N. R., Narayan, K. L., & Reddy, B. R. (2015). A mathematical study of an infectious disease model with time delay in CTL response. Global Journal of Pure and Applied Mathematics (GJPAM), 11.
[11]. Kuang, Y. (Ed.). (1993). Delay Differential Equations: With Applications in Population Dynamics (Vol. 191). Academic Press.
[12]. Kumar, R., Narayan, K. L., & Reddy, B. R. (2017). Mathematical Study of Epidemic Models (Doctor Dissertation, JNTU Hyderabad).
[13]. Murray, J. D. (2002). Mathematical Biology - I: An Introduction, 3rd Edition. Springer Publication.
[14]. Nokes, D. J., & Swinton, J. (1995). The control of childhood viral infections by pulse vaccination. Mathematical Medicine and Biology, 12(1), 29-53.
[15]. Paparao, A., & Narayan, L. K. (2017). Dynamics of a prey predator and competitor model with time delay. International Journal of Ecology & Development, 32(1), 75-86.
[16]. Rao, A. D., Vali, K. S., & Paparao, A. (2017). Dynamics of directly transmitted viral microparasite model. International Journal of Ecology & Development, 32(4), 88-97.
[17]. Zhou, X., & Cui, J. (2011). Global stability of the viral dynamics with Crowley-Martin functional response. Bulletin of the Korean Mathematical Society, 48(3), 555-574.
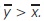 . Numerical simulation is carried out using MATLAB with two delay kernels in support of stability analysis.
. Numerical simulation is carried out using MATLAB with two delay kernels in support of stability analysis.