i-manager Publications

i-manager's Journal on Mathematics (JMAT)

Current Issue Vol. 13 Issue 2

Mathematical Modeling of Higher Overtone Vibrational Frequencies in Dichlorine Monoxide
Some Types of Generalized Closed and Generalized Star Closed Sets in Topological Ordered Spaces
Optimizing Capsule Endoscopy Detection: A Deep Learning Approach with L-Softmax and Laplacian-SGD
Kernel Ideals in Semigroups
Modeling the Dynamics of Covid-19 with the Inclusion of Treatment, Vaccination and Natural Cure
Calculation of Combined Vibrational Frequencies in Cl₂O using Lie Algebraic Method

Most Cited

Volume 7 Issue 2 April - June 2018

Research Article

Proof of Beal's Conjecture and Fermat Last Theorem using Contra Positive Method

Vinay Kumar*

Professor, Vivekananda School of IT, VIPS, GGSIPU, New Delhi, India.

Kumar. V. (2018). Proof of Beal's Conjecture and Fermat Last Theorem using Contra Positive Method. i-manager’s Journal on Mathematics, 7(2), 1-7. https://doi.org/10.26634/jmat.7.2.14127

Abstract

“If A^x + B^y = C^z , for integers A, B, C ≥2 and integers x, y, z greater than 2 , then A, B, C must have a common prime factor”. The statement is known as Beal's conjecture (Rubin & Silverberg, 1994). Without loss of generality, integers B and C can be expressed in terms of A. Assuming B = A + m and C = A + n, the present study proves the conjecture for all the four cases: i) m = 0, n = 0; ii) m = 0, n≠ 0; iii) m≠0, n = 0; and iv) m≠0, n ≠0. A, B, and C can be ordered (sequenced) in six different ways. A theorem that is proved for one sequence, the same theorem can easily be proved for other five sequences. Contrapositive approach together with integer division algorithm is used to prove the conjecture. Contrapositive statement of Beal's x conjecture is “if A, B, and C have no common prime factor then 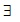no integers A, B, C and integers x, y, z > 2 such that A^x + B^y = C^z”. Some basic and fundamental properties of quadratic equation are also used in the proof.

References

[1]. Aczel, A. D. (1996). Fermat's Last Theorem: Unlocking the Secret of an Ancient Mathematical Problem. N. Y.:Dell Publishing.

[2]. Boston, N. (1995). A Taylor-made plug for Wiles' proof. The College Mathematics Journal, 26(2), 100-105.

[3]. Cornell, G., Silverman, J., and Stevens, G., (eds.) (1997). Modular Forms and Fermat's Last Theorem. Springer- Verlag.

[4]. Granville, A., & Monagan, M. B. (1988). The first case of Fermat's last theorem is true for all prime exponents up to 714,591,416,091,389. Transactions of the American Mathematical Society, 306(1), 329-359.

[5]. Ireland, K., & Rosen, M. (1990). A Classical Introduction to Modern Number Theory (Vol. 84). Springer Science & Business Media.

nd [6]. Jacobson, N. (1989). Basic Algebra II, 2 Ed. New York: W. H. Freeman.

[7]. Kumar, V. (2010). Restricted backtracked algorithm for Hamiltonian circuit in undirected graph. BIJIT-BVICAM's International Journal of Information Technology, 2(2), 23-32.

[8]. Kumar, V. (2012). Mathematics Is Science: A topic revisited in context of FCS of India. International Journal of Modern Education and Computer Science, 4(6), 17-26.

[9]. Kumar, V. (2014). Proof of Fermat last theorem based on odd even classification of integers. Int. J. Open Problems Compt. Math., 7(4), 23-34.

[10]. Kumar, V., (2015). Discrete Mathematics. New Delhi: BPB Publication.

[11]. Mauldin, R. D. (1997). A generalization of Fermat's Last Theorem: The Beal conjecture and prize problem. Notices of the American Mathematical Society, 44(11), 1436-1437.

[12]. Radford, L., & Peirce, C. S. (2006, November). Algebraic thinking and the generalization of patterns: A semiotic th perspective. In Proceedings of the 28 Conference of the International Group for the Psychology of Mathematics

Education, North American Chapter (Vol. 1, pp. 2-21).

[13]. Ribenboim, P. (1999). Fermat's Last Theorem for Amateurs. New York: Springer-Verlag.

[14]. Rubin, K., & Silverberg, A. (1994). A report on Wiles' Cambridge lectures. Bulletin of the American Mathematical Society, 31(1), 15-38.

[15]. Silverman, J. H. (1986). Heights and elliptic curves. In Arithmetic Geometry (pp. 253-265). Springer, New York, NY.

rd [16]. Stewart, I., & Tall, D. (2002). Algebraic Number Theory and Fermat's Last Theorem, 3 Ed. AK Peters/CRC Press.

[17]. Washington, L. C. (1997). Introduction to Cyclotomic Fields (Vol. 83). Springer Science & Business Media.

[18]. Wiles, A. (1995). Modular elliptic curves and Fermat's last theorem. Annals of Mathematics, 141(3), 443-551.

[19]. Zelator, K. (2011). Integer Roots of Quadratic and Cubic Polynomials with Integer Coefficients. arXiv preprint arXiv:1110.6110.

Full Article (HTML)

Pdf

Research Paper

Strong and Δ - Convergence Theorems using Modified Proximal Point Algorithm in CAt(0) Spaces

Apurva Kumar Das* , Shailesh Dhar Diwan, Samir Dashputre*

* Lecturer, Department of Mathematics, Government Polytechnic Sukma, Chhattisgarh, India.

Associate Professor, Department of Mathematics, Government Engineering College, Raipur, Chhattisgarh, India.

* Assistant Professor, Department of Mathematics, Government College Arjunda, Balod, Chhattisgarh, India.

Das. A.K., Diwan. S.D., and Dashputre. S. (2018). Strong and Δ - Convergence Theorems using Modified Proximal Point Algorithm in CAt(0) Spaces. i-manager’s Journal on Mathematics, 7(2), 8-16. https://doi.org/10.26634/jmat.7.2.13999

Abstract

Let (X, d) be a complete CAT(0) space and f∶ X → (-∞, ∞] be a proper convex and lower semi-continuous function. Suppose T be a nonexpansive mapping on X such that Ω=F(T) ⋂ argmin_(yϵX) f(y) is nonempty. The purpose of this paper is to define a modified proximal point algorithm and prove the existence of a sequence proposed by the authors converges to Ω. In this paper, they prove strong and Δ-convergence theorems with their proposed modified proximal point algorithm in CAT(0) spaces.

References

[1]. Adler, R. L., Dedieu, J. P., Margulies, J. Y., Martens, M., & Shub, M. (2002). Newton's method on Riemannian manifolds and a geometric model for the human spine. IMA Journal of Numerical Analysis, 22(3), 359-390.

[2]. Ambrosio, L., Gigli, N., & Savaré, G. (2008). Gradient Flows: In Metric Spaces and in the Space of Probability Measures. Springer Science & Business Media.

[3]. Ariza-Ruiz, D., Leuştean, L., & López-Acedo, G. (2014). Firmly nonexpansive mappings in classes of geodesic spaces. Transactions of the American Mathematical Society, 366(8), 4299-4322.

[4]. Bačák, M. (2013). The proximal point algorithm in metric spaces. Israel Journal of Mathematics, 194(2), 689-701.

[5]. Bačák, M. (2014). Computing medians and means in Hadamard spaces. SIAM Journal on Optimization, 24(3), 1542- 1566.

[6]. Chang, S. S., Yao, J. C., Wang, L., & Qin, L. J. (2016). Some convergence theorems involving proximal point and common fixed points for asymptotically nonexpansive mappings. Fixed Point Theory and Applications, 2016(1), 68.

[7]. Cho, Y. J., Ćirić, L., & Wang, S. H. (2011). Convergence theorems for nonexpansive semigroups in CAT(0) spaces. Nonlinear Analysis: Theory, Methods & Applications, 74(17), 6050-6059.

[8]. Cholamjiak, P., Abdou, A. A., & Cho, Y. J. (2015). Proximal point algorithms involving fixed points of nonexpansive mappings in CAT (0) spaces. Fixed Point Theory and Applications, 2015(1), 227.

[9]. Dhompongsa, S., & Panyanak, B. (2008). On ∆-convergence theorems in CAT(0) spaces. Computers & Mathematics with Applications, 56(10), 2572-2579.

[10]. Dhompongsa, S., Kirk, W. A., & Sims, B. (2006). Fixed points of uniformly Lipschitzian mappings. Nonlinear Analysis: Theory, Methods & Applications, 65(4), 762-772.

[11]. Ferreira, O. P., & Oliveira, P. R. (2002). Proximal point algorithm on Riemannian manifolds. Optimization, 51(2), 257-270.

[12]. Fukhar-ud-din, H. (2013). Strong convergence of an Ishikawa-type algorithm in CAT(0) spaces. Fixed Point Theory and Applications, 2013, 1-11.

[13]. Ishikawa, S. (1974). Fixed points by a new iteration method. Proceedings of the American Mathematical Society, 44(1), 147-150.

[14]. Jost, J. (1995). Convex functionals and generalized harmonic maps into spaces of non positive curvature. Commentarii Mathematici Helvetici, 70(1), 659-673.

[15]. Kirk, W. A. (2003, February). Geodesic geometry and fixed point theory. In Seminar of Mathematical Analysis (Malaga/Seville, 2002/2003) (Vol. 64, pp. 195-225).

[16]. Laokul, T., & Panyanak, B. (2009). Approximating fixed points of nonexpansive mappings in CAT(0) spaces. International Journal of Mathematical Analysis, 3(27), 1305-1315.

[17]. Li, C., López, G., & Martín-Márquez, V. (2009). Monotone vector fields and the proximal point algorithm on Hadamard manifolds. Journal of the London Mathematical Society, 79(3), 663-683.

[18]. Mann, W. R. (1953). Mean value methods in iteration. Proceedings of the American Mathematical Society, 4(3), 506- 510.

[19]. Martinet, B. (1970). Brève communication. Régularisation d'inéquations variationnelles par approximations successives. Revue française d'informatique et de recherche opérationnelle. Série rouge, 4(R3), 154-158.

[20]. Mayer, U. F. (1998). Gradient flows on nonpositively curved metric spaces and harmonic maps. Communications in Analysis and Geometry, 6(2), 199-253.

[21]. Nanjaras, B., & Panyanak, B. (2010). Demiclosed principle for asymptotically nonexpansive mappings in CAT(0) spaces. Fixed Point Theory and Applications, 2010(1), 268780.

[22]. Osilike, M. O., & Aniagbosor, S. C. (2000). Weak and strong convergence theorems for fixed points of asymptotically nonexpensive mappings. Mathematical and Computer Modelling, 32(10), 1181-1191.

[23]. Quiroz, E. P., & Oliveira, P. R. (2009). Proximal point methods for quasiconvex and convex functions with Bregman distances on Hadamard manifolds. J. Convex Anal., 16(1), 49-69.

[24]. Rockafellar, R. T. (1976). Monotone operators and the proximal point algorithm. SIAM Journal on Control and Optimization, 14(5), 877-898.

[25]. Senter, H. F., & Dotson, W. G. (1974). Approximating fixed points of nonexpansive mappings. Proceedings of the American Mathematical Society, 44(2), 375-380.

[26]. Smith, S. T. (1994). Optimization techniques on Riemannian manifolds. Fields Institute Communications, 3(3), 113-135.

[27]. Udriste, C. (1994). Convex Functions and Optimization Methods on Riemannian Manifolds (Vol. 297). Springer Science & Business Media.

[28]. Wang, J. H., & Li, C. (2009). Convergence of the family of Euler-Halley type methods on Riemannian manifolds under

the g-condition. Taiwanese Journal of Mathematics, 13(2A), 585-606.

[29]. Wang, J. H., & López, G. (2011). Modified proximal point algorithms on Hadamard manifolds. Optimization, 60(6), 697- 708.

Full Article (HTML)

Pdf

Research Paper

Constrained Scalar Valued Dynamic Games and Symmetric Duality for Multi Objective Variational Problem

L. Venkateswara Reddy* , Devanandam. Dola, B. Satyanarayana*

* Professor, Department of Information Technology, Sree Vidyanikethan Engineering College (Autonomous), Tirupati, Andhra Pradesh, India.

Lecturer and Head, Department of Mathematics, Dharma Apparao College, Nuzivid, Krishna (Dt), Andhra Pradesh, India.

* Professor, Department of Mathematics, Acharya Nagarjuna University, Nagarjuna Nagar, Andhra Pradesh, India.

Reddy. L.V., Dola. D., and Satyanarayana. B. (2018). Constrained Scalar Valued Dynamic Games and Symmetric Duality for Multi Objective Variational Problem. i-manager’s Journal on Mathematics, 7(2), 17-23. https://doi.org/10.26634/jmat.7.2.14678

Abstract

In this paper, a certain constrained scalar valued dynamic game is formulated and shown to be equivalent to a pair of multi-objective symmetric dual variational problem. These are more generation formulations then those studied easier. Further, various duality results were obtained in this context under generalized invexity conditions.

References

[1]. Chandra, S., Mond B., & Smart, I. (1919). Constrained games and symmetric duality with pseudo- invexity. Opsearch 1919, 27(1), 14-30.

[2]. Charnes, A. (1953). Constrained games and linear programming. Proceedings of the National Academy of Sciences. (Vol.39, No.7, pp.639-641).

[3]. Corley, H. W. (1976). Games with vector pay-offs. J. Opt. Theory Appl., 47, 491-498.

[4]. Cottle, R. W. (1963). An Infinite Game with a Convex-Concave Payoff Kernel.

[5]. Husain, I., & Ahmad, B. (2012). Constrained dynamic game and symmetric duality for variational problems. Journal of Mathematics and System Science, 2, 171-176.

[6]. Husain, I., & Jain, V. K. (2013). Constrained vector-valued dynamic game and symmetric duality for multiobjective variational problems. Open Operational Research Journal, 7, 1-10.

[7]. Kawaguchi, T., Maruyama, V. (1976). A note on mini-max (Max-min) programming. Manag Sci, 22, 670-676.

[8]. Khan, Z. A., & Hanson, M. A. (1997). On ratio invexity in mathematical programming. Journal of Mathematical Analysis and Applications, 205(2), 330-336.

[9]. Mond, B., & Weir, T. (1981). Generalized concavity and duality. Generalized Concavity in Optimization and Economics, 263-279.

[10]. Mond, B., Chandra, S., & Prasad, M. V. D. (1987). Constrained games and symmetric duality. Opsearch, 24, 69-77.

[11]. Mond, B., Hanson, M. A. (1968). Symmetric duality for variational problems. J. Math. Anal. Appl., 23(1), 161-172.

[12]. Prasad, M. D., & Sreenivas, P. C. (1997). Vector valued non zero sum games and non linear programming. Opsearch, 34(3), 180-185.

Full Article (HTML)

Pdf

Research Paper

Influence of Viscous Dissipation on Radiative and Conducting Fluid Past an Accelerated Plate

D. Ravi Kumar* , Gary**

* Research Scholar, Department of Mathematics, Rayalaseema Univesity, Kurnool, Andhra Pradesh, India.

** Professor, Department of Mathematics, K. L. University, Vaddeswaram, Guntur, Andhra Pradesh. India.

Kumar. D.R., and Reddy. K.J. (2018). Influence of Viscous Dissipation on Radiative and Conducting Fluid Past an Accelerated Plate. i-manager’s Journal on Mathematics, 7(2), 24-31. https://doi.org/10.26634/jmat.7.2.14679

Abstract

An unsteady free convective, chemically reactive, radiation absorbing, viscous dissipative fluid past an exponentially accelerated vertical porous plate in the presence of and Soret and Dufour effects is considered. The set of nondimensional governing equations along with boundary conditions are solved numerically using finite difference method. The characteristics of pertinent physical parameters on flow quantities are examined numerically by using graphs. For the substantial interest, the fluctuations in skin friction, Nusselt number and Sherwood number are also deals through tables.

References

[1]. Ahmed, S., & Batin, A. (2014). Magnetohydrodynamic heat and mass transfer flow with induced magnetic field and viscous dissipative effects. Latin American Applied Research, 44(1), 09-17.

[2]. Anjalidevi, S. P., & Kandasamy, R. (1999). Effects of chemical reaction, heat and mass transfer on laminar flow along a semi infinite horizontal plate. Heat and Mass Transfer, 35(6), 465-467.

[3]. Babu, K. R., Parandhama, A., Raju, K. V., Raju, M. C., & Narayana, P. S. (2017). Unsteady MHD free convective flow of a visco-elastic fluid past an infinite vertical porous moving plate with variable temperature and concentration. International Journal of Applied and Computational Mathematics, 3(4), 3411-3431.

[4]. Badruddin, I. A., Zainal, Z. A., Narayana, P. A., & Seetharamu, K. N. (2006). Heat transfer by radiation and natural convection through a vertical annulus embedded in porous medium. International Communications in Heat and Mass Transfer, 33(4), 500-507.

[5]. Barik, R. N. (2014). Chemical reaction and radiation effects of mhd free convective flow past an impulsively moving vertical plate with ramped wall temperature and concentration. European Journal of Advances in Engineering and Technology, 1(2), 56-68.

[6]. Bhargava, R., Sharma, R., & Bég, O. A. (2009). Oscillatory chemically-reacting MHD free convection heat and mass transfer in a porous medium with Soret and Dufour effects: Finite element modeling. Int. J. Appl. Math. Mech., 5(6), 15-37.

[7]. Chen, C. H. (2004). Combined heat and mass transfer in MHD free convection from a vertical surface with Ohmic heating and viscous dissipation. International Journal of Engineering Science, 42(7), 699-713.

[8]. Das, U. N., Deka, R., & Soundalgekar, V. M. (1994). Effects of mass transfer on flow past an impulsively started infinite vertical plate with constant heat flux and chemical reaction. Forschung im Ingenieurwesen, 60(10), 284-287.

[9]. Hayat, T., Qasim, M., & Abbas, Z. (2010). Radiation and mass transfer effects on the magneto hydrodynamic unsteady flow induced by a stretching sheet. Zeitschrift für Naturforschung A, 65(3), 231-239.

[10]. Jordán, J. Z. (2007). Network simulation method applied to radiation and viscous dissipation effects on MHD unsteady free convection over vertical porous plate. Applied Mathematical Modelling, 31(9), 2019-2033.

[11]. Kafousias, N. G., Nanousis, N. D., & Georgantopoulos, G. A. (1979). Free convection effects on the stokes problem for an infinite vertical limiting surface with constant suction. Astrophys. Space Science, 64(2), 391-399.

[12]. Kim, Y. J., & Fedorov, A. G. (2003). Transient mixed radiative convection flow of a micropolar fluid past a moving, semiinfinite vertical porous plate. International Journal of Heat and Mass Transfer, 46(10), 1751-1758.

[13]. Kinyanjui, M., Kwanza, J. K., & Uppal, S. M. (2001). Magnetohydrodynamic free convection heat and mass transfer of a heat generating fluid past an impulsively started infinite vertical porous plate with Hall current and radiation absorption. Enegyr Conversion and Management, 42(8), 917-931.

[14]. Loganathan, P., & Sivapoornapriya, C. (2016). Ohmic heating and viscous dissipation effects over a vertical plate in the presence of porous medium. Journal of Applied Fluid Mechanics, 9(1), 225-232.

[15]. Malik, M. Y., Khan, I., Hussain, A., & Salahuddin, T. (2015). Mixed convection flow of MHD Eyring-Powell nanofluid over a stretching sheet: A numerical study. AIP Advances, 5(11), 117118.

[16]. Mukhopadhyay, S. (2009). Effect of thermal radiation on unsteady mixed convection flow and heat transfer over a porous stretching surface in porous medium. International Journal of Heat and Mass Transfer, 52(13-14), 3261-3265.

[17]. Postelnicu, A. (2007). Influence of chemical reaction on heat and mass transfer by natural convection from vertical surfaces in porous media considering Soret and Dufour effects. Heat and Mass Transfer, 43(6), 595-602.

[18]. Prasad, V. R., & Reddy, N. B. (2008). Radiation and mass transfer effects on anunsteady MHD convection flow past a semi–infinite vertical permeable moving plate embedded in a porous medium with viscous dissipation, Indian J. Pure and Appl. Phys., 46, 81-92.

[19]. Praveena, D., Varma, S. V. K., Veeresh, C., & Raju, M. C. (2017). Chemical reaction and heat source effect on MHD free convection flow of a micropolar fluid through a porous medium over a semi-infinite moving plate with constant heat and mass flux. Journal of Information and Optimization Sciences, 38(8), 1325-1345.

[20]. Raju, C. S. K., Babu, M. J., Sandeep, N., Sugunamma, V., & Reddy, J. R. (2015). Radiation and Soret effects of MHD nanofluid flow over a moving vertical moving plate in porous medium. Chemical and Process Engineering Research, 30, 9- 23.

[21]. Raju, C. S. K., Sanjeevi, P., Raju, M. C., Ibrahim, S. M., Lorenzini, G., & Lorenzini, E. (2017). The flow of magneto hydrodynamic Maxwell nanofluid over a cylinder with Cattaneo-Christov heat flux model. Continuum Mechanics and Thermodynamics, 29(6), 1347-1363.

[22]. Raju, K. V., Raju, C. S. K., Mamata, B., & Raju, M. C. (2017). The flow of hyperbolic tangent fluid over exponentially stretching cylinder with heat source or sink. Research Journal of Science and Technology, 9(4), 576-582.

[23]. Raju, M. C., & Varma, S. V. K. (2014). Soret effects due to natural convection in a non-Newtonian fluid flow in porous medium with heat and mass transfer. Journal of Naval Architecture and Marine Engineering, 11(2), 147-156.

[24]. Raju, M. C., Varma, S. V. K., & Chamkha, A. J. (2016). Unsteady free convection flow past a periodically accelerated vertical plate with Newtonian heating. International Journal of Numerical Methods for Heat & Fluid Flow, 26(7), 2119-2138.

[25]. Raptis, A. (1998). Radiation and free convection flow through a porous medium. International Communications in Heat and Mass Transfer, 25(2), 289-295.

[26]. Raptis, A., Tzivanidis, G., & Kafousias, N. (1981). Free convection and mass transfer flow through a porous medium bounded by an infinite vertical limiting surface with constant suction. Letters in Heat and Mass Transfer, 8(5), 417-424.

[27]. Reddy, L. R., Raju, M. C., Raju, G. S. S., & Ibrahim, S. M. (2017). Chemical reaction and thermal radiation effects on MHD micropolar fluid past a stretching sheet embedded in a non-Darcian porous medium. Journal of Computational and Applied Research in Mechanical Engineering, 6(2), 27-46.

[28]. Reddy, P. C., Raju, M. C., & Raju, G. S. S. (2016). Free convective heat and mass transfer flow of heat generating nanofluid past a vertical moving porous plate in conducting field. Special Topics & Reviews in Porous Media - An International Journal, 7(2), 161-180.

[29]. Reddy, P. C., Raju, M. C., Raju, G. S. S., & Reddy, C. M. (2017). Diffusion thermo and thermal diffusion effects on MHD free convection flow of Rivlin-Ericksen fluid past a semi infinite vertical plate. Bulletin of Pure & Applied Sciences- Mathematics and Statistics, 36(2), 266-284.

[30]. Reddy, P. R. K., & Raju, M. C. (2017a). Heat and mass transfer characteristics on Newtonian fluid over a vertical porous plate in conducting field with ramped boundary condition. International Journal of Current Advanced Research, 6(10), 6831-6842.

[31]. Reddy, P. R. K., & Raju, M. C. (2017b). Combined constant heat and mass flux effect on MHD free convective flow through a porous medium bounded by a vertical surface in presence of chemical reaction and radiation. Bulletin of Pure & Applied Sciences-Mathematics and Statistics, 36(2), 152-164.

[32]. Reddy, P. R. K. (2017). Thermal diffusion effects on MHD free convective heat absorbing fluid with variable temperature and concentration. Journal of Global Research in Mathematical Archives (JGRMA), 4(11), 120-135.

[33]. Reddy, S. H., Raju, M. C., & Reddy, E. K. (2016). Soret and Dufour effects on radiation absorption fluid in the presence of exponentially varying temperature and concentration in conducting field. Special Topics & Reviews in Porous Media - An International Journal, 7(2), 115-129.

[34]. Reddy, T. S., Raju, M. C., & Varma, S. V. K. (2012). The effect of slip condition, radiation and chemical reaction on unsteady MHD periodic flow of a viscous fluid through saturated porous medium in a planer channel. i-manager's Journal on Mathematics, 1(1), 18-28.

[35]. Sattar, M. A., & Kalim, H. (1996). Unsteady free-convection interaction with thermal radiation in a boundary layer flow past a vertical porous plate. J. Math. Phys. Sci., 30(1), 25-37.

[36]. Seddeek, M. A., Darwish, A. A., & Abdelmeguid, M. S. (2007). Effects of chemical reaction and variable viscosity on hydromagnetic mixed convection heat and mass transfer for Hiemenz flow through porous media with radiation. Communications in Nonlinear Science and Numerical Simulation, 12(2), 195-213.

[37]. Singh, A. K. (1983). Finite difference analysis of MHD free-convection flow past an accelerated vertical porous plate. Astrophysics and Space Science, 94(2), 395-400.

[38]. Srinivasacharya, D., & Reddy, G. S. (2016). Chemical reaction and radiation effects on mixed convection heat and mass transfer over a vertical plate in power-law fluid saturated porous medium. Journal of the Egyptian Mathematical Society, 24(1), 108-115.

[39]. Sulochana, C., Sandeep, N., Sugunamma, V., & Kumar, B. R. (2016). Aligned magnetic field and cross-diffusion effects of a nanofluid over an exponentially stretching surface in porous medium. Applied Nanoscience, 6(5), 737-746.

[40]. Tsai, R., & Huang, J. S. (2009). Heat and mass transfer for Soret and Dufour's effects on Hiemenz flow through porous medium onto a stretching surface. International Journal of Heat and Mass Transfer, 52(9-10), 2399-2406.

[41]. Umamheswar, M., Varma, S. V. K., & Raju, M. C. (2016). Numerical study of Magneto-Convective and radiation absorption fluid flow past an exponentially accelerated vertical porous plate with variable temperature and concentration in the presence of Soret and Dufour effects. IOSR Journal of Mathematics, 12(2), 109-120.

[42]. Veeresh, C., Varma, S. V. K., Kumar, A. G. V., Umamaheswar, M., & Raju, M. C. (2017). Joule heating and thermal diffusion effects on MHD radiative and convective Casson fluid flow past an oscillating semi-infinite vertical porous plate. Frontiers in Heat and Mass Transfer, 8(1). 1-8.

Full Article (HTML)

Pdf

Research Paper

Thermal Diffusion and Radiation Effects on Magnetocasson Fluid Flow Past A Vertical Porous Plate

K. Venkateswara Raju* , M. C. Raju, V. Ravi Kumar*, G. S. S. Raju****

* Assistant Professor, Department of Mathematics, Sree Vidyanikethan Engineering College (Autonomous), A. Rangampet, Tirupati, Andhra Pradesh, India.

Coordinator Research and Development, Department of Mathematics, Annamacharya Institute of Technology and Sciences (Autonomous), Rajampet, , Andhra Pradesh, India.

* Assistant Professor, Department of Mathematics, Annamacharya Institute of Technology and Sciences (Autonomous), Rajampet, Andhra Pradesh, India.

****The Professor and Head, Department of Mathematics, JNTU College of Engineering (Autonomous), Pulivendula, Kadapa (Dt), Andhra Pradesh, India.

Raju. K.V., Raju, M.C., Kumar. V.R., and Raju. G.S.S. (2018). Thermal Diffusion and Radiation Effects on Magnetocasson Fluid Flow Past A Vertical Porous Plate. i-manager’s Journal on Mathematics, 7(2), 32-46. https://doi.org/10.26634/jmat.7.2.14680

Abstract

In this manuscript thermal diffusion and radiation effects on magneto-Casson fluid flow past a vertical porous plate with chemical reaction is studied. The non-dimensional governing equations for momentum, energy and concentration equations have been solved by using perturbation techniques. The expressions for skin friction, Nusselt number and Sherwood number are also obtained. The effects of various physical parameters like chemical reaction parameter, Casson parameter, magnetic parameter, radiation parameter, Soret number, Schmidt number, Grashof number, Prandtl number, and modified Grashof number have been discussed in detailed through graphs and tables.

References

[1]. Ahmed, N., & Sarmah, H. K. (2009). Thermal radiation effect on a transient MHD flow with mass transfer past an impulsively fixed infinite vertical plate. Int. J. Appl. Math. Mech., 5(5), 87-98.

[2]. Bhattacharyya, K., & Layek, G. C. (2011). Effects of suction/blowing on steady boundary layer stagnation-point flow and heat transfer towards a shrinking sheet with thermal radiation. International Journal of Heat and Mass Transfer, 54(1-3), 302- 307.

[3]. Dash, R. K., Mehta, K. N., & Jayaraman, G. (1996). Casson fluid flow in a pipe filled with a homogeneous porous medium. International Journal of Engineering Science, 34(10), 1145-1156.

[4]. Jain, N. C., & Singh, H. (2012). Hall and thermal radiative effects on an unsteady rotating free convection slip flow along a porous vertical moving plate. International Journal of Applied Mechanics and Engineering, 17(1), 53-70.

[5]. Kumar, B. R., Kumar, T. S., & Kumar, A. G. V. (2015). Thermal diffusion and radiation effects on unsteady free convection flow in the presence of magnetic field fixed relative to the fluid or to the plate, Frontier in Heat and Mass Transfer, 6 (12), 1-9.

[6]. Kumar, V. R., Raj, M. C., Raju, G. S. S., & Varma, S. V. K. (2016). Thermal diffusive free convective radiating flow over an impulsively started vertical porous plate in conducting field. Journal of Physical Mathematics, 7(1), 1-8.

[7]. Kumar, V. R., Raju, M. C, Raju, G. S. S Varma, S. V. K. (2013). Magnetic field effects on transient free convection flow through porous medium past an impulsively started vertically plate with fluctuating temperature and mass diffusion, International Journal of Mathematical Archive, 4(6), 198-206.

[8]. Mustafa, M., Hayat, T., Pop, I., & Aziz, A. (2011). Unsteady boundary layer flow of a Casson fluid due to an impulsively started moving flat plate. Heat Transfer-Asian Research, 40(6), 563-576.

[9]. Oyelakin, I. S., Mondal, S., & Sibanda, P. (2016). Unsteady Casson non-fluid flow over a stretching sheet with thermal radiation, convective, and slip boundary conditions. Alexandria Engineering Journal, 55(2), 1025-1035.

[10]. Prakash, J., Balamurugan, K. S., & Varma, S. V. (2014). Thermo-diffusion and chemical reaction effects on MHD three dimensional free convective Couette flow. Walailak Journal of Science and Technology (WJST), 12(9), 805-830.

[11]. Raju, K. V. S., Reddy, T. S., Raju, M. C., Narayana, P. S., & Venkataramana, S. (2014). MHD convective flow through porous medium in a horizontal channel with insulated and impermeable bottom wall in the presence of viscous dissipation and Joule heating. Ain Shams Engineering Journal, 5(2), 543-551.

[12]. Raju, R. S., Reddy, G. J., Rao, J. A., & Rashidi, M. M. (2016). Thermal diffusion and diffusion thermo effects on an unsteady heat and mass transfer magneto hydrodynamic natural convection Couette flow using FEM. Journal of Computational Design and Engineering, 3(4), 349-362.

[13]. Raju, R. S., Sudhakar, K., & Rangamma, M. (2013). The effects of thermal radiation and Heat source on an unsteady MHD free convection flow past an infinite vertical plate with thermal diffusion and diffusion thermo. Journal of The Institutionof Engineers (India): Series C, 94(2), 175-186.

[14]. Rashidi, M. M., Hayat, T., Erfani, E., Pour, S. M., & Hendi, A. A. (2011). Simultaneous effects of partial slip and thermaldiffusion and diffusion-thermo on steady MHD convective flow due to a rotating disk. Communications in Nonlinear Science and Numerical Simulation, 16(11), 4303-4317.

[15]. Ravikumar, V., Raju, M. C., & Raju, G. S. S. (2014). Combined effects of heat absorption and MHD on convective Rivlin- Ericksen flow past a semi-infinite vertical porous plate with variable temperature and suction. Ain Shams Engineering Journal, 5(3), 867-875.

[16]. Ravikumar, V., Raju, M. C., & Raju, G. S. S. (2015). Theoretical investigation of an unsteady MHD free convection heat and mass transfer flow of a non-Newtonian fluid flow past a permeable moving vertical plate in the presence of thermal diffusion and heat sink. In International Journal of Engineering Research in Africa (Vol. 16, pp. 90-109). Trans Tech Publications.

[17]. Reddy, B. M. G. V., & Raju, M. C. (2015). Thermal diffusion and radiation effects on MHD convective chemically reactive dusty fluid-flow past a vertical porous plate with heat absorption. Elixir Appl. Math. (Elixir International Journal), 88, 36320- 36327.

[18]. Reddy, N. A., Varma, S. V. K., & Raju, M. C. (2010). Thermo diffusion and chemical effects with simultaneous thermal and mass diffusion in MHD mixed convection flow with ohmic heating. Journal of Naval Architecture and Marine Engineering, 6(2), 84-93.

[19]. Reddy, G. J., Raju, R. S., Manideep, P., & Rao, J. O. (2016). Thermal diffusion thermo effects on unsteady MHD fluid flow past a moving vertical plate embedded in porous medium in the presence of hall current and rotating system. Transaction of A. Razmadze Mathematical Institute, 170(2), 243-265.

[20]. Seddeek, M. A. (2004). Thermal-diffusion and diffusion-thermo effects on mixed free-forced convective flow and mass transfer over an accelerating surface with a heat source in the presence of suction and blowing in the case of variable viscosity. Acta Mechanica, 172(1-2), 83-94.

[21]. Sharma, P. K. (2005). Fluctuating thermal and mass diffusion on unsteady free convection flow past a vertical plate in slip-flow regime. Latin American Applied Research, 35(4), 313-319.

[22]. Shehzad, S. A., Hayat, T., Qasim, M., & Asghar, S. (2013). Effects of mass transfer on MHD flow of Casson fluid with chemical reaction and suction. Brazilian Journal of Chemical Engineering, 30(1), 187-195.

[23]. Shivaiah. S. & Rao. J. A. (2012). On an unsteady MHD free convection flow past a vertical porous plate in the presence of suction or injection. Theoret. Appl. Mech., 39, (2), 185-208.

[24]. Srinivas, S., Reddy, A. S., Ramamohan, T. R., & Shukla, A. K. (2016). Thermal-diffusion and diffusion-thermo effects on MHD flow of viscous fluid between expanding or contracting rotating porous disks with viscous dissipation. Journal of the Egyptian Mathematical Society, 24(1), 100-107.

i-manager's Journal on Mathematics (JMAT)

Current Issue Vol. 13 Issue 2

Most Read

Most Cited

Volume 7 Issue 2 April - June 2018

Proof of Beal's Conjecture and Fermat Last Theorem using Contra Positive Method

Vinay Kumar*

Professor, Vivekananda School of IT, VIPS, GGSIPU, New Delhi, India.

Kumar. V. (2018). Proof of Beal's Conjecture and Fermat Last Theorem using Contra Positive Method. i-manager’s Journal on Mathematics, 7(2), 1-7. https://doi.org/10.26634/jmat.7.2.14127

Abstract

References

Full Article (HTML)

Pdf

Strong and Δ - Convergence Theorems using Modified Proximal Point Algorithm in CAt(0) Spaces

Apurva Kumar Das* , Shailesh Dhar Diwan**, Samir Dashputre***

Das. A.K., Diwan. S.D., and Dashputre. S. (2018). Strong and Δ - Convergence Theorems using Modified Proximal Point Algorithm in CAt(0) Spaces. i-manager’s Journal on Mathematics, 7(2), 8-16. https://doi.org/10.26634/jmat.7.2.13999

Abstract

References

Full Article (HTML)

Pdf

Constrained Scalar Valued Dynamic Games and Symmetric Duality for Multi Objective Variational Problem

L. Venkateswara Reddy* , Devanandam. Dola**, B. Satyanarayana***

Reddy. L.V., Dola. D., and Satyanarayana. B. (2018). Constrained Scalar Valued Dynamic Games and Symmetric Duality for Multi Objective Variational Problem. i-manager’s Journal on Mathematics, 7(2), 17-23. https://doi.org/10.26634/jmat.7.2.14678

Abstract

References

Full Article (HTML)

Pdf

Influence of Viscous Dissipation on Radiative and Conducting Fluid Past an Accelerated Plate

D. Ravi Kumar* , Gary**

* Research Scholar, Department of Mathematics, Rayalaseema Univesity, Kurnool, Andhra Pradesh, India. ** Professor, Department of Mathematics, K. L. University, Vaddeswaram, Guntur, Andhra Pradesh. India.

Kumar. D.R., and Reddy. K.J. (2018). Influence of Viscous Dissipation on Radiative and Conducting Fluid Past an Accelerated Plate. i-manager’s Journal on Mathematics, 7(2), 24-31. https://doi.org/10.26634/jmat.7.2.14679

Abstract

References

Full Article (HTML)

Pdf

Thermal Diffusion and Radiation Effects on Magnetocasson Fluid Flow Past A Vertical Porous Plate

K. Venkateswara Raju* , M. C. Raju**, V. Ravi Kumar***, G. S. S. Raju****

Raju. K.V., Raju, M.C., Kumar. V.R., and Raju. G.S.S. (2018). Thermal Diffusion and Radiation Effects on Magnetocasson Fluid Flow Past A Vertical Porous Plate. i-manager’s Journal on Mathematics, 7(2), 32-46. https://doi.org/10.26634/jmat.7.2.14680

Abstract

References

Full Article (HTML)

Pdf

Apurva Kumar Das* , Shailesh Dhar Diwan, Samir Dashputre*

L. Venkateswara Reddy* , Devanandam. Dola, B. Satyanarayana*

* Research Scholar, Department of Mathematics, Rayalaseema Univesity, Kurnool, Andhra Pradesh, India.

** Professor, Department of Mathematics, K. L. University, Vaddeswaram, Guntur, Andhra Pradesh. India.

K. Venkateswara Raju* , M. C. Raju, V. Ravi Kumar*, G. S. S. Raju****