i-manager Publications

i-manager's Journal on Mathematics (JMAT)

Current Issue Vol. 13 Issue 2

Mathematical Modeling of Higher Overtone Vibrational Frequencies in Dichlorine Monoxide
Some Types of Generalized Closed and Generalized Star Closed Sets in Topological Ordered Spaces
Optimizing Capsule Endoscopy Detection: A Deep Learning Approach with L-Softmax and Laplacian-SGD
Kernel Ideals in Semigroups
Modeling the Dynamics of Covid-19 with the Inclusion of Treatment, Vaccination and Natural Cure
Calculation of Combined Vibrational Frequencies in Cl₂O using Lie Algebraic Method

Most Cited

Volume 3 Issue 1 January - March 2014

Article

Some New Generalized Difference Sequence Spaces with Modular Sequence Space

Gülcan Atici* , Cigdem A. BEKTAS**

* Department of Mathematics, Mus Alparslan University, Mus, Turkey.

** Department of Mathematics, Firat University, Elazig, Turkey.

Atici, G., and Bektas, C.A. (2014). Some New Generalized Difference Sequence Spaces With Modular Sequence Space. i-manager’s Journal on Mathematics, 3(1), 1-6. https://doi.org/10.26634/jmat.3.1.2937

Abstract

In this paper, the authors define the sequence space used in a sequence of Orlicz functions 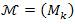, generalized difference sequence 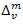and seminorm q. They examine some topological properties of this space.

References

[1]. Bektas, Ç. A., (2004). On some difference sequence spaces defined by Orlicz functions, Southeast Asian Bull. Math., Vol.28, pp.195-202.

[2]. Et, M. and Çolak, R., (1995). On generalized difference sequence spaces, Soochow J. Math., Vol.21, pp.377-386.

[3]. Et, M. and Esi, A., (2000). On Köthe-Toeplitz duals of generalized difference sequence spaces, Bull. Malaysian Math. Sc. Soc., Vol.23, pp.25-32.

[4]. Kamthan, P. K. and Gupta, M., (1981). Sequence Spaces and Series, Marcel Dekkar.

[5]. Kizmaz, H., (1981). On certain sequence spaces, Canad. Math. Bull., Vol.24, pp.169-176.

[6]. Lindenstrauss, J. and Tzafriri, L., (1965). On Orlicz sequence spaces, Israel J. Math., Vol.10, pp.379-390.

[7]. Wilansky, A. (1964). Functional Analysis, Blaisdell Publishing Company, New York.

Full Article (HTML)

Pdf

Article

Collections of Statements Related to Domination Parameters in Graphs

D. R. Robert Joan* , Y. Sheeja**

* Assistant Professor of Mathematics in Christian College of Education, Marthandam, Tamilnadu, India.

** Assistant Professor, Department of mathematics, M.E.T. College of Education, Chenbagaramanputhoor, Tamilnadu, India.

Joan, D. R. R., and Sheeja, Y. (2014). Collections Of Statements Related To Domination Parameters In Graphs. i-manager’s Journal on Mathematics, 3(1), 7-13. https://doi.org/10.26634/jmat.3.1.2938

Abstract

A dominating set D ⊆ V is said to be a nilprivate neighbour dominating set if, for every vertex u in D has no private neighbour in V-D. The nilprivate neighbour domination number γ_npn(G) is the minimum cardinality of a nilprivate npn neighbour dominating set. A dominating set D⊆ V of a graph G is a non-split dominating set if the induced sub-graph 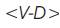is connected. The non-split domination number γ_ns(G) is the minimum cardinality of a non-split dominating set of G. A dominating set D ⊆ V of a graph G is a strong non-split dominating set if the induced sub-graph 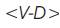is complete. The strong non-split domination number sns(G) is the minimum cardinality of a strong non-split dominating set of G. The dominating set D ⊆ V of a graph G is a vertex set dominating set if for any set S ⊆V-D, there exists a vertex vD such that the induced sub-graph 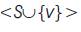is connected.The vertex set domination number γ_vs(G) is the minimum cardinality of a vs vertex set dominating set of G. A dominating set D of a graph G = (V, E) is a strong non-split dominating set if the induced sub-graph 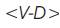is complete. The strong non-split domination number γ_sns(G) of G is the minimum cardinality of a strong sns non-split dominating set of G. Here, the authors state some definitions and statements related to the Nilprivate neighbour domination and strong non-split domination number in graphs. In conclusion, the authors state the domination of strong non-split domination graphs.

References

[1]. Cockayne, E.J., Dawes, R.M. & Hedetniemi, S. T. (1977). Total domination in graphs. Networks, Vol.10, pp.211-219.

[2]. Haynes, T. W., Hedetniemi, S.T., & Slater, P.J. (1998). Fundamentals of Domination in Graphs. Marcel Dekker, Inc. New York,

[3]. Joseph, J., & Arumugam, S. (1992). On connected cut free domination in graphs. Indian Journal of Pure and Applied Mathematics, Vol.23, pp.643-647.

[4]. Kulli, V.R., & Janakiram, B. (1997). The Split domination number of a graph. Graph theory notes of New York, New York: pp.16 - 19.

[5]. Sampathkumar, E. (1989). The global domination number of a graph. Journal of Mathematics and Physical Science, Vol.23, pp.377-385.

Full Article (HTML)

Pdf

Research Paper

Calculating Tri–Symmetrical Analytics: A Guide Into The In–Depth Processes Associated With The Post Hoc Advanced Statistical Metrics Used To Determine The Value Of Significant Tri–Squared Tests

James Edward Osler II*

North Carolina Central University, Durham, North Carolina.

Osler, J. E., II. (2014). Calculating Tri–Symmetrical Analytics: A Guide into the In–Depth Processes Associated with the Post Hoc Advanced Statistical Metrics used to Determine the Value of Significant Tri–Squared Tests. i-manager’s Journal on Mathematics, 3(1), 14-26. https://doi.org/10.26634/jmat.3.1.2939

Abstract

This monograph provides an epistemological guide for the Post Hoc Tri–Symmetrical Omnibus Test for the Tri–Squared Test. In this guide, Advanced Tri–Symmetrical Tests are explained in great detail and are calculated using sample data. Tri–Symmetrical Omnibus Tests use Tri–Squared correlation metrics and Tri–Squared association analytics to further discern information regarding the outcomes of a statistically significant Tri–Squared Test. In this narrative, multiple sequential Tri–Symmetrical mathematical models are illustrated in a tabular format to demonstrate the entire process of advanced Tri–Symmetrical inquiry.

References

[1]. Apostol, T. M. (1967). Calculus, second edition, Volume one: One-variable calculus, with an introduction to linear algebra. Waltham, MA: Blaisdell.

[2]. Kant, I. (2007). Critique of pure reason (based on Max Müller's translation). P. Classics a Division of Pearson PLC. New York, NY.

[3]. Osler, J. E. (2012). Trichotomy–Squared – A novel mixed methods test and research procedure designed to analyze, transform, and compare qualitative and quantitative data for education scientists who are administrators, practitioners, teachers, and technologists. i-manager's Journal on Mathematics, 1 (3), Jul-Sep 2012, Print ISSN 2277-5129, E-ISSN 2277- 5137, pp. 23–31.

[4]. Osler, J. E. (2013). The Psychometrics of Educational Science: Designing Trichotomous Inventive Investigative Instruments for Qualitative and Quantitative for Inquiry. i-manager's Journal on School Educational Technology, 8 (3), Dec-Feb 2013, Print ISSN 0973-2217, E-ISSN 2230-7133, pp. 15–22.

[5]. Osler, J. E. (2013). The Psychological Efficacy of Education as a Science through Personal, Professional, and Contextual Inquiry of the Affective Learning Domain. i-manager's Journal on Educational Psychology, 6 (4), Feb-Apr 2013, Print ISSN 0973-8827, E-ISSN 2230-7141, pp. 36–41.

[6]. Osler, J. E. (2013). Algorithmic Triangulation Metrics for Innovative Data Transformation: Defining the Application Process of the Tri–Squared Test. i-manager's Journal on Mathematics, 2 (2), Apr-Jun 2013, Print ISSN 2277-5129, E-ISSN 2277-5137, pp. 10–16.

[7]. Rust, J. & Golombok, S. (1989). Modern psychometrics: The science of psychological assessment (2nd ed.). Florence, KY, US: Taylor & Frances/Routledge. Sensagent: Retrieved, May 9, 2012: http://dictionary.sensagent.com/trichotomy+ (mathematics)/en-en/

[8]. Singh, S. (1997). Fermat's enigma: The epic quest to solve the world's greatest mathematical problem. A. Books a Division of Random House. New York, NY.

Full Article (HTML)

Pdf

Research Paper

Synchronization Of Three Dimensional Cancer Model With Lorenz System Using A Robust Adaptive Sliding Mode Controller

Mohammad *

Department of General Requirements, College of Applied Sciences, Nizwa, Oman.

Shahzad, M. (2014). Synchronization of Three Dimensional Cancer Model with Lorenz System using A Robust Adaptive Sliding Mode Controller. i-manager’s Journal on Mathematics, 3(1), 27-34. https://doi.org/10.26634/jmat.3.1.2940

Abstract

This paper investigates the synchronization of chaotic Three Dimensional Cancer Model (TDCM) with Lorenz System (LS) using a Robust Adaptive Sliding Mode Controller (RASMC) together with uncertainties, external disturbances and fully unknown parameters. The technique used for synchronization is based on simple suitable sliding surface, which includes synchronization errors and appropriate update laws to tackle the uncertainties, external disturbances and unknown parameters. All simulations to achieve the synchronization for the proposed technique for the two non-identical systems under consideration are being done using Mathematica.

References

[1]. Fujisaka, H. & Yamada, T. (1983). Stability Theory of Synchronized Motion in Coupled-Oscillator Systems, Prog. Theor. Phys., Vol.69 (1), pp.32-37.

[2]. Pecora, L. M. & Carroll, T. L. (1990). Synchronization in Chaotic Systems, Phys. Rev. Lett., Vol.64, pp.821-824.

[3]. Xiang, W. & Huangpu, Y. (2010). Second-order terminal sliding mode controller for a class of chaotic systems with unmatched uncertainties, Commun Nonlinear Sci Numer Simulat., Vol.15, pp.3241–3247.

[4]. Rafikov, M. & Balthazar, J. M. (2008). On control and synchronization in chaotic and hyperchaotic systems via linear feedback control, Commun Nonlinear Sci Numer Simulat., Vol.13, pp.1246–1255.

[5]. Bowong, S. (2007). Adaptive synchronization between two different chaotic dynamical systems, Commun Nonlinear Sci Numer Simulat., Vol.12, pp.976–985.

[6]. Chen, H., Sheu, G., Lin, Y. & Chen, C. (2009). Chaos synchronization between two different chaotic systems via nonlinear feedback control, Nonlinear Anal., Vol.70, pp.4393–4401.

[7]. Yassen, M. T. (2007). Controlling, synchronization and tracking chaotic Liu system using active backstepping design, Phys Lett A. Vol.360, pp.582–587.

[8]. Wang, F. & Liu, C. (2007). Synchronization of unified chaotic system based on passive control, Physica D Vol.225, pp.55–60.

[9]. Yau, H. & Shieh, C. (2008). Chaos synchronization using fuzzy logic controller, Nonlinear Anal: RWA. Vol.9, pp.1800–1810.

[10]. Chang, W. (2009). PID control for chaotic synchronization using particle swarm optimization, Chaos Soliton Fract. Vol.39, pp.910–917.

[11]. Sun, Y. (2009). Chaos synchronization of uncertain Genesio–Tesi chaotic systems with dead zone nonlinearity, Phys Lett A. Vol.373, pp.3273–3276.

[12]. Jianwen, F., Ling, H., Chen, X., Austin, F. & Geng, W. (2010). Synchronizing the noise-perturbed Genesio chaotic system by sliding mode control, Commun Nonlinear Sci Numer Simulat., Vol.15, pp.2546–2551.

[13]. Feki, M. (2009). Sliding mode control and synchronization of chaotic systems with parametric uncertainties, Chaos Soliton Fract., Vol.41, pp.1390–1400.

[14]. Lin, C., Peng, Y. & Lin, M. (2009). CMAC-based adaptive backstepping synchronization of uncertain chaotic systems, Chaos Soliton Fract., Vol.42, pp.981–988.

[15]. Ahmadi, A. A. & Majd, V. J. (2009). Robust synchronization of a class of uncertain chaotic systems, Chaos Soliton Fract. Vol.42, pp.1092–1096.

[16]. Asheghan, M. M. & Beheshti, M. T. H. (2009). An LMI approach to robust synchronization of a class of chaotic systems with gain variations, Chaos Soliton Fract., Vol.42, pp.1106–1111.

[17]. Zhang, H. & Ma, X. (2004). Synchronization of uncertain chaotic systems with parameters perturbation via active control, Chaos Soliton Fract. Vol.21, pp.39–47.

[18]. Cai, N., Jing, Y. & Zhang, S. (2010). Modified projective synchronization of chaotic systems with disturbances via active sliding mode control, Commun Nonlinear Sci Numer Simulat. Vol.15, pp.1613–1620.

[19]. Kebriaei, H. & Yazdanpanah, M. J. (2010). Robust adaptive synchronization of different uncertain chaotic systems subject to input nonlinearity, Commun Nonlinear Sci Numer Simulat. Vol.15, pp.430–441.

[20]. Chen, C. (2009). Quadratic optimal neural fuzzy control for synchronization of uncertain chaotic systems, Expert Syst Appl., Vol.36, pp.11827–11835.

[21]. Li, W. & Chang, K. (2009). Robust synchronization of drive-response chaotic systems via adaptive sliding mode control, Chaos Soliton Fract. Vol.39, pp.2086–2092.

[22]. Wang, H., Han, Z., Xie, Q. & Zhang, W. (2009). Finite-time chaos synchronization of unified chaotic system with uncertain parameters, Commun Nonlinear Sci Numer Simulat. Vol.14, pp.2239–2247.

[23]. Zhang, G., Liu, Z. & Zhang, J. (2008). Adaptive synchronization of a class of continuous chaotic systems with uncertain parameters, Phys Lett A. Vol.372, pp.447–450.

[24]. Ma, J., Zhang, A., Xia, Y. & Zhang, L. (2010). Optimize design of adaptive synchronization controllers and parameter observers in different hyperchaotic systems, Appl Math Comput., Vol.215, pp.3318–3326.

[25]. El-Gohary A. (2006). Optimal synchronization of Rossler system with complete uncertain parameters, Chaos Soliton Fract. Vol.27, pp.345–355.

[26]. Hwang, E., Hyun, C., Kim, E. & Park, M. (2009). Fuzzy model based adaptive synchronization of uncertain chaotic systems: robust tracking control approach, Phys Lett A. Vol.373, pp.1935–1939.

[27]. Yassen, M.T. (2005). Adaptive synchronization of two different uncertain chaotic systems, Phys Lett A. Vol.337, pp.335–341.

[28]. Chen, X. & Lu, J. (2007). Adaptive synchronization of different chaotic systems with fully unknown parameters, Phys Lett A. Vol.364, pp.123–128.

[29]. Salarieh, H. & Shahrokhi, M. (2008). Adaptive synchronization of two different chaotic systems with time varying unknown parameters, Chaos Soliton Fract. Vol.37, pp.125–136.

[30]. Yan, J., Hung, M., Chiang, T. & Yang, Y. (2006). Robust synchronization of chaotic systems via adaptive sliding mode control, Phys Lett A. Vol.356, pp.220–225.

[31]. Wang, C. & Ge, S. S. (2001). Adaptive synchronization of uncertain chaotic systems via backstepping design, Chaos Soliton Fract. Vol.12, pp.1199–1206.

[32]. Aghababa, M. P. & Heydari, A. (2012). Chaos synchronization between two different chaotic systems with uncertainties, external disturbances, unknown parameters and input nonlinearities, Applied Mathematical Modelling. Vol.36, pp.1639–1652.

[33]. Aghababa, M. P. & Akbari, M. E. (2012). A chattering-free robust adaptive sliding mode controller for synchronization of two different chaotic systems with unknown uncertainties and external disturbances, Applied Mathematics and Computation., Vol.218, pp.5757–5768.

[34]. Pourmahmood, M., Khanmohammadi, S. & Alizadeh, G. (2011). Synchronization of two different uncertain chaotic systems with unknown parameters using a robust adaptive sliding mode controller, Commun Nonlinear Sci Numer Simulat. Vol.16, pp.2853–2868.

[35]. Itik, M. & Banks, S. P. (2010). Chaos in a three dimensional cancer model, IJBC., Vol.20, pp.71-79.

[36]. Kim, C. J. & Chwa, D. (2011). Synchronization of the bi directionally coupled unified chaotic system via sum of squares method, Chaos., Vol.21, pp.013104.

Full Article (HTML)

Pdf

Research Paper

Mass Transfer Effects On Nonlinear MHD Boundary Layer Flow Of Liquid Metal Over A Porous Nonlinearly Stretching Surface Through Porous Medium With Nonlinear Radiation

s mohammed ibrahim*

Department of Mathematics, Priyadarshini College of Engineering & Technology, Nellore, Andhra Pradesh, India

Ibrahim, S.M. (2014). Mass Transfer Effects On Nonlinear MHD Boundary Layer Flow Of Liquid Metal Over A Porous Nonlinearly Stretching Surface Through Porous Medium With Nonlinear Radiation. i-manager’s Journal on Mathematics, 3(1), 35-45. https://doi.org/10.26634/jmat.3.1.2941

Abstract

The paper investigates the nonlinear radiation effects on two-dimensional, steady MHD laminar boundary layer flow with heat and mass transfer characteristic of an incompressible, viscous, electrically conducting fluid over a nonlinearly stretching surface through a porous medium. The liquid metal is assumed to be gray, emitting, and absorbing, but nonscattering medium. The basic equations governing the flow are in the form of partial differential equations and have been reduced to a set of non-linear ordinary differential equations by applying suitable similarity transformations. The problem is tackled numerically using shooting techniques with fourth order Runge-Kutta integration scheme. Pertinent results with respect to embedded parameters are displayed graphically for the velocity, temperature, concentration, skin-friction coefficient, rate of heat transfer and rate of mass transfer profiles and were discussed quantitatively.

References

[1]. M Arunachalam and N.R Rajappa (1978). Thermal boundary layer in liquid metals with variable thermal conductivity, Appl. Sci. Res, Vol. 34, pp. 179- 185.

[2]. B. Lubarsky and S.J Kaufman (1955). Review of Experimental investigation of Liquid metal heat transfer, Report NACA TN 3336.

[3]. R.N Lyon (1951). Liquid Metal heat transfer coefficient, Chem. Eng. Progr., Vol. 47, No. 2, pp. 75-79.

[4]. B. C. Sakiadios (1961). Boundary layer behaviour on continuous solid surfaces, American Institute of Chemical Engineers, Vol. 7, pp. 26–28.

[5]. L. E. Erickson, L.T. Fan, and V. G. Fox (1966). Heat and mass transfer on a moving continuous moving surface, Industrial & Engineering Chemistry Fundamentals, Vol. 5, pp. 19–25.

[6]. J. E. Danberg and K. S. Fansler (1979). A nonsimilar moving wall boundary-layer problem, Quarterly of Applied Mathematics, Vol. 34, pp. 305–309.

[7]. P. S. Gupta and A. S. Gupta (1977). Heat and mass transfer on a stretching sheet with suction or blowing, The Canadian Journal of Chemical Engineering, Vol. 55, pp. 744–746.

[8]. V. G. Fox, L. E. Erickson, and L.T. Fan (1969). Heat and mass transfer on a moving continuous flat plate with suction or injection, American Institute of Chemical Engineers, Vol. 15, pp. 327–333.

[9]. K. R. Rajagopal, T. Y. Na, and A. S. Gupta (1984). Flow of a viscoelastic fluid over a stretching sheet, Rheologica Acta, Vol. 23, No. 2, pp. 213–215.

[10]. W. C. Troy, E. A. Overman, II, G. B. Ermentrout, and J. P. Keener (1987). Uniqueness of flow of a second order fluid past a stretching sheet, Quarterly of Applied Mathematics, Vol. 44, No. 4, pp. 753–755.

[11]. K. Vajravelu and T. Roper (1999). Flow and heat transfer in a second grade fluid over a stretching sheet, International Journal of Non-Linear Mechanics, Vol. 34, No. 6, pp. 1031–1036.

[12]. K. Vajravelu (2001). Viscous flow over a nonlinearly stretching sheet, Applied Mathematics and Computation, Vol. 124, No. 3, pp. 281–288.

[13]. R. Cortell (2007). MHD flow and mass transfer of an electrically conducting fluid of second grade in a porous medium over a stretching sheet with chemically reactive species, Chemical Engineering and Processing, Vol. 46, No. 8, pp. 721–728.

[14]. R. Cortell (2007). Viscous flow and heat transfer over a nonlinearly stretching sheet, Applied Mathematics and Computation, Vol. 184, No. 2, pp. 864–873.

[15]. R. Cortell (2008). Effects of viscous dissipation and radiation on the thermal boundary layer over a nonlinearly stretching sheet, Physics Letters, Section A, Vol. 372, No. 5, pp. 631–636.

[16]. D.A Nield and A Bejan (1999). Convection in Porous Media, 2nd Edition. Springer, New York.

[17]. K. Vafai (2000). Handbook of Porous Media. Marcel Dekker, New York.

[18]. I. Pop and D. B. Ingham, (2001). Convective Heat Transfer: Mathematical and Computational Modelling of Viscous Fluids and Porous Media, Pergamon, Elsevier Science, Oxford, UK, 2001.

[19]. R.N Barik., G.C Dash and P.K Rath (2012). Heat and Mass transfer on MHD flow through a porous medium over a stretching surface with heat source, Mathematical Theory and Modeling, Vol.2, No. 7, pp. 49-59.

[20]. S.M Alharbi., M.A.A Bazid and S.El Gendy (2010). Heat and Mass transfer in MHD visco-elastic fluid flow through a porous medium over a stretching sheet with chemical reaction, Applied Mathematics, Vol. 1, pp. 446-455.

[21]. Anuar Ishak (2011). MHD Boundary layer flow due to an exponentially stretching sheet with radiation effect, Sains Malaysiana, Vol. 40, No. 4,pp. 391-395.

[22]. O.D Makinde, and A. Ogulu (2008). The effect of thermal radiation on the heat and mass transfer flow of a variable viscosity fluid past a vertical porous plate permeated by a transverse magnetic field, Chemical Engineering Communications, Vol.195, No. 12, pp. 1575-1584.

[23]. S. Shateyi and M Petersen (2008). Thermal radiation and buoyancy effects on heat and mass tra over a semi-infinite stretching surface with suction and blowing, Journal of Applied Mathematics, Vol.2, pp. 1–12 .

[24]. A.J Chamkha., H.S Thkhar and V.M Soundalgekar (2001). Radiation effects on free convection flow past a semi- infinite vertical plate with mass transfer, Chemical Engineering Journal, Vol. 84,pp. 335-342.

[25]. E.M.A. Elbashbeshy (2000). Free convection flow with variable viscosity and thermal diffusivity along a vertical plate in the presence of magnetic field, International Journal of Engineering Science, Vol.38. No.2, pp. 207-213.

[26]. A. Raptis and C. Perdikis (2006). Viscous flow over a non-linearly stretching sheet in the presence of a chemical reaction and magnetic field, International Journal of Non-Linear Mechanics, Vol.41, No.4, pp. 527–529.

[27]. S. Awang Kechil and I. Hashim (2008). Series solution of flow over nonlinearly stretching sheet with chemical reaction and magnetic field, Physics Letters, Section A, Vol. 372, No. 13, pp. 2258–2263.

[28]. Z. Abbas and T. Hayat (2008). Radiation effects on MHD flow in a porous space, International Journal of Heat and Mass Transfer, Vol. 51, No. 5-6, pp. 1024–1033.

[29]. E.M. Ouaf Mahmoud (2005). Exact solution of thermal radiation on MHD flow over a stretching porous sheet, Applied Mathematics and Computation., Vol. 170, pp. 1117-1125.

[30]. S. Mukhopadhyay, G.C. Layek and R.S.R. Gorla (2007). MHD combined convective flow and heat transfer past a porous stretching surface, International Journal of Fluid Mechanics Research, Vol. 34(3),pp. 244-257.

[31]. A.D.M Gururaj and C. Pavithra (2013). Nonlinear MHD boundary layer of a liquid metal with heat transfer over a porous stretching surface with nonlinear radiation effects, Advances in Applied Science Research, Vol. 4, No. 2, pp. 77-92.

[32]. S.P Anjali Devi and A.D.M Gururaj (2012). Effects of variable viscosity and nonlinear radiation on MHD flow with heat transfer over a surface with a power-law velocity, Advances in Applied Science Research, Vol. 3, No. 1, pp. 319-334.

[33]. S Mohammed Ibrahim., T Sankar Reddy and N Bhaskar Reddy ( 2012). Radiation and chemical reaction effects on MHD convective flow past a moving vertical porous plate, Int. J. of Applied Mathematical Analysis and Applications, Vol. 7, No.1, pp. 1-16.

[34]. T. C. Chaim. Hydromagnetic flow over a surface stretching with a power law velocity, International Journal of Engineering Science, Vol. 33, No. 3, 1995, pp. 429-435.

[35]. M. E. Ali. Heat transfer characteristics of a continuous stretching surface, Heat and Mass Transfer, Vol. 29, No. 4, pp. 227–234, 1994.

[36]. Michael Modest, (2003). Radiative Heat Transfer, 2nd ed. McGraw-Hill, New York.

[37]. M.A Hossain and I Pop, (1999). Effect of heat transfer on compressible boundary layer flow past a sphere, Zeitschrift fur Angewandte Mathematik und Mechanik (ZAMM), Vol. 79, pp. 715-720.

[38]. M.K Jain., S.R.K Iyengar and R.K Jain (1985). Numerical methods for scientific and engineering computations, Wiley Eastern Ltd., New Delhi, India.

i-manager's Journal on Mathematics (JMAT)

Current Issue Vol. 13 Issue 2

Most Read

Most Cited

Volume 3 Issue 1 January - March 2014

Some New Generalized Difference Sequence Spaces with Modular Sequence Space

Gülcan Atici* , Cigdem A. BEKTAS**

* Department of Mathematics, Mus Alparslan University, Mus, Turkey. ** Department of Mathematics, Firat University, Elazig, Turkey.

Atici, G., and Bektas, C.A. (2014). Some New Generalized Difference Sequence Spaces With Modular Sequence Space. i-manager’s Journal on Mathematics, 3(1), 1-6. https://doi.org/10.26634/jmat.3.1.2937

Abstract

References

Full Article (HTML)

Pdf

Collections of Statements Related to Domination Parameters in Graphs

D. R. Robert Joan* , Y. Sheeja**

* Assistant Professor of Mathematics in Christian College of Education, Marthandam, Tamilnadu, India. ** Assistant Professor, Department of mathematics, M.E.T. College of Education, Chenbagaramanputhoor, Tamilnadu, India.

Joan, D. R. R., and Sheeja, Y. (2014). Collections Of Statements Related To Domination Parameters In Graphs. i-manager’s Journal on Mathematics, 3(1), 7-13. https://doi.org/10.26634/jmat.3.1.2938

Abstract

References

Full Article (HTML)

Pdf

Calculating Tri–Symmetrical Analytics: A Guide Into The In–Depth Processes Associated With The Post Hoc Advanced Statistical Metrics Used To Determine The Value Of Significant Tri–Squared Tests

James Edward Osler II*

North Carolina Central University, Durham, North Carolina.

Abstract

References

Full Article (HTML)

Pdf

Synchronization Of Three Dimensional Cancer Model With Lorenz System Using A Robust Adaptive Sliding Mode Controller

Mohammad *

Department of General Requirements, College of Applied Sciences, Nizwa, Oman.

Shahzad, M. (2014). Synchronization of Three Dimensional Cancer Model with Lorenz System using A Robust Adaptive Sliding Mode Controller. i-manager’s Journal on Mathematics, 3(1), 27-34. https://doi.org/10.26634/jmat.3.1.2940

Abstract

References

Full Article (HTML)

Pdf

Mass Transfer Effects On Nonlinear MHD Boundary Layer Flow Of Liquid Metal Over A Porous Nonlinearly Stretching Surface Through Porous Medium With Nonlinear Radiation

s mohammed ibrahim*

Department of Mathematics, Priyadarshini College of Engineering & Technology, Nellore, Andhra Pradesh, India

Ibrahim, S.M. (2014). Mass Transfer Effects On Nonlinear MHD Boundary Layer Flow Of Liquid Metal Over A Porous Nonlinearly Stretching Surface Through Porous Medium With Nonlinear Radiation. i-manager’s Journal on Mathematics, 3(1), 35-45. https://doi.org/10.26634/jmat.3.1.2941

Abstract

References

Full Article (HTML)

Pdf

* Department of Mathematics, Mus Alparslan University, Mus, Turkey.

** Department of Mathematics, Firat University, Elazig, Turkey.

* Assistant Professor of Mathematics in Christian College of Education, Marthandam, Tamilnadu, India.

** Assistant Professor, Department of mathematics, M.E.T. College of Education, Chenbagaramanputhoor, Tamilnadu, India.