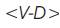 is complete. The strong non-split domination number sns(G) is the minimum cardinality of a strong non-split dominating set of G. The dominating set D ⊆ V of a graph G is a vertex set dominating set if for any set S ⊆V-D, there exists a vertex vD such that the induced sub-graph
is complete. The strong non-split domination number sns(G) is the minimum cardinality of a strong non-split dominating set of G. The dominating set D ⊆ V of a graph G is a vertex set dominating set if for any set S ⊆V-D, there exists a vertex vD such that the induced sub-graph 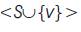 is connected.The vertex set domination number γvs(G) is the minimum cardinality of a vs vertex set dominating set of G. A dominating set D of a graph G = (V, E) is a strong non-split dominating set if the induced sub-graph
is connected.The vertex set domination number γvs(G) is the minimum cardinality of a vs vertex set dominating set of G. A dominating set D of a graph G = (V, E) is a strong non-split dominating set if the induced sub-graph 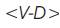 is complete. The strong non-split domination number γsns(G) of G is the minimum cardinality of a strong sns non-split dominating set of G. Here, the authors state some definitions and statements related to the Nilprivate neighbour domination and strong non-split domination number in graphs. In conclusion, the authors state the domination of strong non-split domination graphs.
">
is complete. The strong non-split domination number γsns(G) of G is the minimum cardinality of a strong sns non-split dominating set of G. Here, the authors state some definitions and statements related to the Nilprivate neighbour domination and strong non-split domination number in graphs. In conclusion, the authors state the domination of strong non-split domination graphs.
">
A dominating set D ⊆ V is said to be a nilprivate neighbour dominating set if, for every vertex u in D has no private neighbour in V-D. The nilprivate neighbour domination number γnpn(G) is the minimum cardinality of a nilprivate npn neighbour dominating set. A dominating set D⊆ V of a graph G is a non-split dominating set if the induced sub-graph 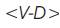 is connected. The non-split domination number γns(G) is the minimum cardinality of a non-split dominating set of G. A dominating set D ⊆ V of a graph G is a strong non-split dominating set if the induced sub-graph
is connected. The non-split domination number γns(G) is the minimum cardinality of a non-split dominating set of G. A dominating set D ⊆ V of a graph G is a strong non-split dominating set if the induced sub-graph 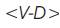 is complete. The strong non-split domination number sns(G) is the minimum cardinality of a strong non-split dominating set of G. The dominating set D ⊆ V of a graph G is a vertex set dominating set if for any set S ⊆V-D, there exists a vertex vD such that the induced sub-graph
is complete. The strong non-split domination number sns(G) is the minimum cardinality of a strong non-split dominating set of G. The dominating set D ⊆ V of a graph G is a vertex set dominating set if for any set S ⊆V-D, there exists a vertex vD such that the induced sub-graph 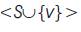 is connected.The vertex set domination number γvs(G) is the minimum cardinality of a vs vertex set dominating set of G. A dominating set D of a graph G = (V, E) is a strong non-split dominating set if the induced sub-graph
is connected.The vertex set domination number γvs(G) is the minimum cardinality of a vs vertex set dominating set of G. A dominating set D of a graph G = (V, E) is a strong non-split dominating set if the induced sub-graph 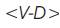 is complete. The strong non-split domination number γsns(G) of G is the minimum cardinality of a strong sns non-split dominating set of G. Here, the authors state some definitions and statements related to the Nilprivate neighbour domination and strong non-split domination number in graphs. In conclusion, the authors state the domination of strong non-split domination graphs.
is complete. The strong non-split domination number γsns(G) of G is the minimum cardinality of a strong sns non-split dominating set of G. Here, the authors state some definitions and statements related to the Nilprivate neighbour domination and strong non-split domination number in graphs. In conclusion, the authors state the domination of strong non-split domination graphs.