Mathematical Modeling of Higher Overtone Vibrational Frequencies in Dichlorine Monoxide
Some Types of Generalized Closed and Generalized Star Closed Sets in Topological Ordered Spaces
Optimizing Capsule Endoscopy Detection: A Deep Learning Approach with L-Softmax and Laplacian-SGD
Kernel Ideals in Semigroups
Modeling the Dynamics of Covid-19 with the Inclusion of Treatment, Vaccination and Natural Cure
Calculation of Combined Vibrational Frequencies in Cl₂O using Lie Algebraic Method
An Introduction to Various Types of Mathematics Teaching Aids
A Simple Method of Numerical Integration for a Class of Singularly Perturbed Two Point Boundary Value Problems
A New Approach to Variant Assignment Problem
A Homotopy Based Method for Nonlinear Fredholm Integral Equations
Proof of Beal's Conjecture and Fermat Last Theorem using Contra Positive Method
Trichotomy–Squared – A Novel Mixed Methods Test and Research Procedure Designed to Analyze, Transform, and Compare Qualitative and Quantitative Data for Education Scientists who are Administrators, Practitioners, Teachers, and Technologists
Algorithmic Triangulation Metrics for Innovative Data Transformation: Defining the Application Process of the Tri–Squared Test
A New Hilbert-Type Inequality In Whole Plane With The Homogeneous Kernel Of Degree 0
Introducing Trinova: “Trichotomous Nomographical Variance” a Post Hoc Advanced Statistical Test of Between and Within Group Variances of Trichotomous Categorical and Outcome Variables of a Significant Tri–Squared Test
Surfaces in R3 with density
In this paper the authors concerned with the concept and the existence of the uniformly stable solution of the functional inclusion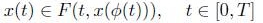 
in the two classes C[0, T] and L1 [0, T].
In this paper, we study biharmonic curves in E3. We give some characterizations for curvature and torsion of a biharmonic curve in E3.
The International Skating Union implemented a new judging system, the International Judging System (IJS), after it was revealed that the previously used 6.0 judging system accommodated for judging bias in figure skating events at the 2002 Olympic Winter Games. The 6.0 judging system required judges to rank figure skaters’ placements in an event relative to the other competitors; a controversy arose in the pairs event at the Olympic Games when it became clear that some of the judges were persuaded to influence the outcome irrespective of the actual performances of the skaters. The new IJS now requires judges to rate each element performed by each skater, without comparison to other skaters’ performances, in an effort to reduce judging bias. The judges’ ratings are then averaged and a decimal score is accordingly assigned for each element. The skaters earn a technical score, computed by finding the sum of the element scores. In this article, the IJS is explained as an application of mathematics, and a skating judging activity suitable for middle grades students is presented. The activity involves students’ rating a pairs team’s performance and computing the team’s score through a simplified version of the IJS.
In this paper, the authors study characterizes null general helices in terms of their curvature and torsion in the Lorentzian Heisenberg group Heis3. They also gave their explicit parametrizations.
This present paper is devoted to investigation of lossy transmissions lines terminated by a nonlinear resistive element. The transmission line is terminated by an R-element with exponential nonlinearity in the V-I characteristic. The reducing of the mixed problem for Telegrapher hyperbolic system to an initial value problem for a nonlinear neutral equation on the boundary is made in [3]. The nonlinearity in the boundary condition is transferred to the neutral equation on the boundary. Then we introduce a suitable operator whose fixed point is an oscillatory solution of the neutral equation. The main existence-uniqueness theorem contains conditions which guarantee that the operator mentioned is contractive one in a uniform space. Finally, we demonstrate how to apply the results obtained to the circuit design.
