Mathematical Modeling of Higher Overtone Vibrational Frequencies in Dichlorine Monoxide
Some Types of Generalized Closed and Generalized Star Closed Sets in Topological Ordered Spaces
Optimizing Capsule Endoscopy Detection: A Deep Learning Approach with L-Softmax and Laplacian-SGD
Kernel Ideals in Semigroups
Modeling the Dynamics of Covid-19 with the Inclusion of Treatment, Vaccination and Natural Cure
Calculation of Combined Vibrational Frequencies in Cl₂O using Lie Algebraic Method
An Introduction to Various Types of Mathematics Teaching Aids
A Simple Method of Numerical Integration for a Class of Singularly Perturbed Two Point Boundary Value Problems
A New Approach to Variant Assignment Problem
A Homotopy Based Method for Nonlinear Fredholm Integral Equations
Proof of Beal's Conjecture and Fermat Last Theorem using Contra Positive Method
Trichotomy–Squared – A Novel Mixed Methods Test and Research Procedure Designed to Analyze, Transform, and Compare Qualitative and Quantitative Data for Education Scientists who are Administrators, Practitioners, Teachers, and Technologists
Algorithmic Triangulation Metrics for Innovative Data Transformation: Defining the Application Process of the Tri–Squared Test
A New Hilbert-Type Inequality In Whole Plane With The Homogeneous Kernel Of Degree 0
Introducing Trinova: “Trichotomous Nomographical Variance” a Post Hoc Advanced Statistical Test of Between and Within Group Variances of Trichotomous Categorical and Outcome Variables of a Significant Tri–Squared Test
Surfaces in R3 with density
This monograph provides an in-depth discourse on a model for the design and construction of digital instruments in the field of Educational Science first detailed in i-managers Journal on Mathematics earlier article. A research engineered computational instrument design model involves the methodology and the metrics used to conduct in-depth research investigations via the innovative Total Transformative Trichotomy-Squared (Tri-Squared) Test. The completion of digital instrumentation of the Tri–Squared will provide researchers with a means of creating qualitative metrics that can be qualitatively analyzed. The creation of a model of digital instruments based on Tri-Squared calculation presents a novel method for in-depth mixed methods research design based upon “Trichotomous Psychometric”. Trichotomous Psychometrics involves the development, deployment, and analysis of Trifold assessments for the holistic transformation of qualitative outcomes into quantitative data. This paper is a continuation of the published article entitled, “The Psychometrics of Educational Science: Designing Trichotomous Inventive Investigative Instruments for Qualitative and Quantitative for Inquiry” published in the i-managers Journal on Education Psychology.
In this paper, the authors have studied some properties of continuity and boundedness of linear mapping in fuzzy anti nnormed spaces. Firstly, the authors have given some definitions and theorem, such as fuzzy anti n-normed , fuzzy anti nnormed space and α - n - norms on fuzzy anti n-normed space, convergent sequence and Cauchy sequence on fuzzy anti n-normed space and fuzzy anti-n-Banach space, open ball and closed ball. The authors have presented some examples by using these definitions. Secondly, the authors have studied linear mapping on fuzzy anti n-normed spaces and the authors redefine fuzzy anti n-continuity and fuzzy anti n-bounded by using previous definitions of contiunity and boundedness. Additionally, the authors have given some definitions, weakly fuzzy anti n-continuous, strongly fuzzy anti ncontinuous, sequentially fuzzy anti n-continuous, using these definitions. Moreover, the authors have given the relationship between fuzzy anti n-continuity and fuzzy anti n-boundedness. Finally, the authors have showed that, T is strongly fuzzy anti n-continuous if and only if T is strongly fuzzy anti n-bounded and, T is weakly fuzzy anti n-continuous if and only if T is weakly fuzzy anti n-bounded.
This is the study of the grade-III fluid having the unidirectional and unsteady flow. Differential equation is solved using perturbation method to get linear forms of the velocities. The velocity u(y,t) is perturbed in ε to get the two-linear Partial Differential Equations (PDE's) in terms of u0(y,t) and u1(y,t). The solution of 1st linear is given in the exponent form f(y) eiat , that gives an ordinary differential equation that is easily solved to get the solution. This solution u0(y,t) is then utilized in Partial Differential Equation of 1st term velocity u1(y,t) and that gives linear Partial Differential Equation in the velocity u1(y,t). The solution of u1(y,t) is given in the exponent form F(y) e3iat , that gives an ordinary differential equation in F(y), that is solved to get the solution of F(y). This gives the perturbed solution for u1(y,t) in the form of F(y). First and zeroth solutions for the velocities give the solution for PDE.
In this paper, the authors have introduced and investigated two subclasses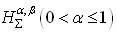
,
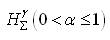of Analytic and Biunivalent functions in the open unit disc Δ. For functions belonging to these classes, the authors have obtained estimates on the first two Taylor-Maclaurin coefficients 
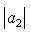and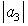 
. The results of this paper will generalize some of the earlier known results.
In this paper, the authors have introduced a new subclass of analytic functions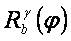
. The main objective of this work is to study the kth root transformations for the functions in some subclasses of analytic functions. The authors have obtained the sharp upper bounds for the coefficient functional 
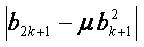corresponding to the Kth root transformation for the function f in this class. Similar results are obtained for the inverse function and for 
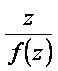. The results will generalize the results obtained by earlier researchers in this direction. This paper will be interesting for the researcher’s working in the area of complex variables.
