i-manager Publications

i-manager's Journal on Mathematics (JMAT)

Current Issue Vol. 13 Issue 2

Mathematical Modeling of Higher Overtone Vibrational Frequencies in Dichlorine Monoxide
Some Types of Generalized Closed and Generalized Star Closed Sets in Topological Ordered Spaces
Optimizing Capsule Endoscopy Detection: A Deep Learning Approach with L-Softmax and Laplacian-SGD
Kernel Ideals in Semigroups
Modeling the Dynamics of Covid-19 with the Inclusion of Treatment, Vaccination and Natural Cure
Calculation of Combined Vibrational Frequencies in Cl₂O using Lie Algebraic Method

Most Cited

Volume 1 Issue 2 April - June 2012

Article

S-α Surfaces Of Biharmonic S-Curves According To Sabban Frame In Heisenberg Group Heis³

Talat Körpinar* , Essin TURHAN**

*-** Firat University, Department of Mathematics, Elazig, Turkey.

Körpinar, T., and Turhan, E. (2012). S-? Surfaces Of Biharmonic S-Curves According To Sabban Frame In Heisenberg Group Heis3. i-manager’s Journal on Mathematics, 1(2), 1-6. https://doi.org/10.26634/jmat.1.2.1844

Abstract

In this paper, we study surfaces according to Sabban frame in the Heisenberg group Heis . We characterize the biharmonic curves in terms of their geodesic curvature and we prove that all of biharmonic curves are helices in the Heisenberg group Heis . Finally, we find explicit parametric equations of surfaces according to Sabban Frame.

References

[1]. M. Babaarslan and Y. Yayli: The characterizations of constant slope surfaces and Bertrand curves, International Journal of the Physical Sciences 6(8) (2011), 1868-1875.

[2]. R. Caddeo and S. Montaldo: Biharmonic submanifolds of S , Internat. J. Math. 12(8) (2001), 867--876.

[3]. B. Y. Chen: Some open problems and conjectures on submanifolds of finite type, Soochow J. Math. 17 (1991), 169--188.

[4]. I. Dimitric: Submanifolds of Em with harmonic mean curvature vector, Bull. Inst. Math. Acad. Sinica 20 (1992), 53--65.

[5]. J. Eells and L. Lemaire: A report on harmonic maps, Bull. London Math. Soc. 10 (1978), 1--68.

[6]. J. Eells and J. H. Sampson: Harmonic mappings of Riemannian manifolds, Amer. J. Math. 86 (1964), 109--160.

[7]. S. Izumiya and N. Takeuchi: Special Curves and Ruled Surfaces, Contributions to Algebra and Geometry 44 (2003), 203- 212.

[8]. G. Y. Jiang: 2-harmonic maps and their first and second variational formulas, Chinese Ann. Math. Ser. A 7(4) (1986), 389-- 402.

[9]. T. Körpinar, E. Turhan: Biharmonic S-Curves According to Sabban Frame in Heisenberg Group Heis , Bol. Soc. Paran. Mat. 31 (1) (2013), 205-211.

[10]. E. Loubeau and S. Montaldo: Biminimal immersions in space forms, preprint, 2004, math.DG/0405320 v1.

[11]. B. O'Neill: Semi-Riemannian Geometry, Academic Press, New York (1983).

[12]. E. Turhan, T. Körpinar: On Characterization Of Timelike Horizontal Biharmonic Curves In The Lorentzian Heisenberg Group Heis , Zeitschrift für Naturforschung A- A Journal of Physical Sciences 65a (2010), 641-648.

[13]. E. Turhan, T. Körpinar: On Characterization Canal Surfaces around Timelike Horizontal Biharmonic Curves in Lorentzian Heisenberg Group Heis , Zeitschrift für Naturforschung A- A Journal of Physical Sciences 66a (2011), 441-449.

Full Article (HTML)

Pdf

Research Paper

The Inverse Surfaces Of Tangent Developables With Respect To S_c(r)

Muhittin Evren Aydin* , Mahmut ERGÜT**

*-** Department of Mathematics, Firat University, Turkey.

Aydin, M.E., and Ergüt, M. (2012). The Inverse Surfaces of Tangent Developables with Respect to S ( R). i-manager’s Journal on Mathematics, 1(2), 7-12. https://doi.org/10.26634/jmat.1.2.1846

Abstract

In this paper, we define the inverse surface of a tangent developable surface with respect to the sphere S_c(r) with the center 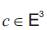and the radius r in 3-dimensional Euclidean space 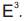We obtain the curvatures, the Christoffel symbols and the shape operator of this inverse surface by the help of these of the tangent developable surface. Morever, we give some necessary and sufficient conditions regarding the inverse surface being flat and minimal.

References

[1]. A. Gray: Modern differential geometry of curves and surfaces with mathematica. CRC Press LLC, 1998.

[2]. D. A. Brannan, M. F. Esplen, J. J. Gray : Geometry, Cambridge Universtiy Press, Cambridge, 1999.

[3]. D. E. Blair: Inversion theory and conformal mapping. American Mathematical Society, 2000.

[4]. E. Ozyilmaz, Y. Yayli: On the closed space-like developable ruled surface, Hadronic J. 23 (4) (2000) 439--456.

[5]. H. S. M. Coexeter: Inversive Geometry, Educational Studies in Mathematics, 3 (1971), 310-321.

[6]. F. Beardona, D. Mindap: Sphere-Preserving Maps in Inversive Geometry. Proceedings of the American Mathematical Society, 130(4) (2001), 987-998.

[7]. PM. do Carmo : Riemann Geometry. Birkhauser, Boston, 1992.

[8]. P. Alegre, K. Arslan, A. Carriazo, C. Murathan and G. Öztürk: Some Special Types of Developable Ruled Surface, Hacettepe Journal of Mathematics and Statistics, 39 (3) (2010), 319 -- 325.

[9]. S. Izumiya, H. Katsumi and T. Yamasaki: The rectifying developable and the spherical Darboux image of a space curve. Geometry and topology of caustics-Caustics '98- Banach Center Publications, 50 (1999), 137-149.

[10]. S. Izumiya and N. Takeuchi: Special curves and ruled surfaces, Applicable Mathematics in the Golden Age (ed., J.C. Misra), Narosa Publishing House, New Delhi, (2003) 305-338.

[11]-: New Special Curves and Developable Surfaces, Turk J Math 28 (2004), 153-163.

Full Article (HTML)

Pdf

Research Paper

On Some New Generalized Difference Sequence Spaces Defined By A Sequence Of Orlicz Functions

Cigdem A. BEKTAS* , Gülcan Atici**

* Department of Mathematics, Firat University, Turkey.

** Department of Mathematics, Mus Alparslan University, Turkey.

Bektaþ, C.A., and Atici, G. (2012). On Some New Generalized Difference Sequence Spaces Defined By A Sequence of Orlicz Functions. i-manager’s Journal on Mathematics, 1(2), 13-19. https://doi.org/10.26634/jmat.1.2.1847

Abstract

In this paper, the authors define the new generalized difference sequence spaces , and . We also study some inclusion relations between these spaces.

References

[1]. Bektas, Ç.A. (2004). On some difference sequence spaces defined by Orlicz functions. Southeast Asian Bulletin of Mathematics, 28, 195-202.

[2]. Et, M., & Çolak, R. (1995). On generalized difference sequence spaces. Soochow J. of Math.21(4), 377-386.

[3]. Et, M.& Esi, A. (2000). On Köthe-Toeplitzduals of generalized difference sequence spaces. Bull. Malaysian Math. Sc. Soc. (2)23, 25-32.

[4]. Et M.,Yee, L.P. & Tripathy, B.C. (2006). Stronglyalmost - summable sequences defined by Orlicz functions. Hokkaido Math. Journal. 35(1), 197-213.

[5]. Kamthan, P.K., & Gupta, M. (1981). Sequence spaces and series. New York: MarcelDekkerInc.

[6]. Kizmaz, H. (1981). On certain,sequence,spaces. Canad Math. Bull. 24, 169-176.

[7]. Leindler, L. (1965). Überdiede la Vallée-Pousinchesummierbarkeitallgemeinerorthogonalreihen. Acta Math. Acad. Sci. Hungar. 16, 375-387.

[8]. Lindenstrauss, J., & Tzafriri, L. (1971). On Orlicz sequence spaces. Israel J. Math. 10, 379-390.

[9]. Wilansky, A. (1984). Summability through Functional Analysis. Nort-Holl and Mathematics studies. 85.

Full Article (HTML)

Pdf

Research Paper

Non-null Special Curves of AW(k)-type in Minkowski 3-Space

Handan Öztekin* , Sezin Aykurt**

* Department of Mathematics, Faculty of Science, Firat University, Elazig, Turkey.

** Department of Mathematics, Faculty of Science and Art, Ahi Evran University, Kirsehir, Turkey

Öztekin, H., and Aykurt, S. (2012). Non-Null Special Curves of Aw(K)-Type in Minkowski 3-Space. i-manager’s Journal on Mathematics, 1(2), 20-25. https://doi.org/10.26634/jmat.1.2.1848

Abstract

In this paper, firstly, we consider non-null curves of -type in -dimensional Minkowski space and obtain some relations between first and second curvatures of them. Then, we give some conditions in order to be non-null Bertrand curve of -type curves with and in . Also, we deal with weak -type and weak -type non-null curves and investigate first curvature for weak .

References

[1]. Arslan, K., Özgür, C., Curves and surfaces of AW(k)-type, Geometry and topology of submanifolds, IX (Valenciennes/Lyon/Leuven, 1997), 21-26, Word Sci. Publishing, River Edge, NJ, 1999.

[2]. Balgetir, H., Bektas, M., Ergüt, M., Bertrand curves for nonnull curves in 3-dimensional Lorentzian space, Hadronic J. 27 (2004) 229-236.

[3]. Ilarslan, K., Nešovic, E., On rectifying curves as centrodes and extremal curves in the Minkowski 3-space. Novi Sad J. Math., 2007, 37(1): 53 - 64.

[4]. Izumiya, S., Takeuchi, N., Generic properties of helices and Bertrand curves, J. Geom. 74 (2002) 97-109.

[5]. Izumiya, S., Takeuchi, N., New special curves and developable surfaces, Turkish J. Math. 28 (2) (2004) 153-163.

[6]. Külahci, M., Bektas, M., Ergüt, M., On Harmonic Curvatures of Null Curves of the AW(k)-type in Lorentzian Space, Z. Naturforsch.63a, 248-252, 2008.

[7]. Külahci, M., Ergüt, M., Bertrand curves of AW(k)-type in Lorentzian space, Nonlinear Analysis, 70(2009),1725-1731.

[8]. Özgür, C., Gezgin, F., On some curves of AW(k)-type, Differ. Geom. Dyn. Syst. 7 (2005) 74-80.

Full Article (HTML)

Pdf

Research Paper

Computational Study of Synchronization and Anti-Synchronization In Mimas-Tethys System

Ayub Khan* , 0**

* Associate Professor, Department of Mathematics, Zakir Husain College, University of Delhi, New Delhi, India.

** Assistant Professor, Department of General Requirements, College of Applied Sciences, Nizwa, Oman.

Khan, A., and Shahzad, M. (2012). Computational Study of Synchronization and Anti-Synchronization in Mimas-Tethys System. i-manager’s Journal on Mathematics, 1(2), 26-33. https://doi.org/10.26634/jmat.1.2.1849

Abstract

In this paper, we have investigated the synchronization and anti-synchronization behaviour of two identical dynamical model of mimas-tethys system (Moons of Saturn) evolving from different initial conditions using the active control technique based on the Lyapunov stability theory and Routh-Hurwitz criteria. The designed controller, with our own choice of the coefficient matrix of the error dynamics that satisfy the Lyapunov stability theory and the Routh-Hurwitz criteria, are found to be effective in the stabilization of the error states at the origin, thereby, achieving synchronization and anti-synchronization between the states variables of two nonlinear dynamical systems under consideration. The results are validated by numerical simulations using mathematica.

References

[1]. Hubler, A.W. (1989). Adaptive control of chaotic system. J. Helv Phys. Acta: 62, 343-346.

[2]. Pecora, L. M., & Carroll, T. L. (1990). Synchronization in chaotic systems. Phys Rev. Lett.: 64, 821-824.

[3]. Carroll, T. M., & Pecora, L. M. (1991). Synchronizing a chaotic system. IEEE Trans. Circuits Systems: 38, 453-456.

[4]. Boccaletti, S., Kurths, J., Osipov, G., Valladares, D. L., & Zhou, C. S. (2002). The synchronization of chaotic systems. Physics Reports: 366, 1-101.

[5]. Chen, G., & Dong, X. (1998). From Chaos to Order: Methodologies, Perspectives and Applications. Singapore: World Scientific.

[6]. Schuster, H. G. (1999). Handbook of Chaos Control. Weinheim: Wiley-VCH.

[7]. Sprott, J. C. (2003). Chaos and Time-Series Analysis. Oxford: Oxford University Press.

[8]. Ott, E., Grebogi, C., & Yorke, J. A. (1990). Controlling chaos. J. Phys. Rev. Lett., 64: 1196-1199.

[9]. Diebner, H. H., & Grond, F. (2005). Usability of synchronization for cognitive modeling. Chaos, Solitons Fractals. 25: 905- 910.

[10]. Pikovsky, A., Rosenblum, M., & Kurths, J. (2001). Synchronization: A Universal Concept in Nonlinear Science, Cambridge: Cambridge University Press.

[11]. González Salas, J. S., Cantón, E. C., Salazar, F. C. O., & Cantón, I. C. (2008). Forced synchronization of a self-sustained chaotic oscillator. Chaos: 18, 023136.

[12]. Li, C., Chen, L., &. Aihara, K. (2008). Impulsive control of stochastic systems with applications in chaos control, chaos synchronization, and neural networks. Chaos: 18, 023132.

[13]. Huang, T., Li, C., & Liao, X. (2007). Synchronization of a class of coupled chaotic delayed systems with parameter mismatch. Chaos: 17, 033121.

[14]. Wang, X.Y., & Wu, X.J. (2006). Tracking control and synchronization of four-dimensional hyperchaotic Rössler system. Chaos: 16, 033121.

[15]. Astakhov, V. V., Anishchenko, V.S., Kapitaniak, T., & Shabunin, A.V. (1997). Synchronization of chaotic oscillators by periodic parametric perturbations. Physica D: 109, 11-16.

[16]. Chua, L.O., Yang, T., Zhong, G.Q., & Wu, C.W. (1996). Adaptive Synchronization of Chua's Oscillators. Int. J. Bifurcation Chaos: 6, 189-201.

[17]. Li, Z., Chen, G., Shi, S., & Han, C. (2003). Robust adaptive tracking control for a class of uncertain chaotic systems. Phys. Lett. A: 310, 40-43.

[18]. Liao, T.L. (1998). Adaptive Synchronization of Two Lorenz Systems. Chaos, Solitons Fractals: 9, 1555-61.

[19]. Wang, Y., Guan, Z. H., & Wen, X. (2004). Adaptive synchronization for Chen chaotic system with fully unknown parameters. Chaos, Solitons Fractals: 19, 899-903.

[20]. Wu, C.W., Yang, T., & Chua, L.O. (1996). On Adaptive Synchronization and Control of Nonlinear Dynamical System. Int. J. Bifurcation Chaos: 6, 455-471.

[21]. Salarieh, H., & Shahrokhi, M. (2008). Adaptive synchronization of two different chaotic systems with time varying unknown parameters. Chaos, Solitons Fractals: 37, 125-136.

[22]. Li, X., Xu, W., & Xiao, Y. (2008). Adaptive tracking control of a class of uncertain chaotic systems in the presence of random perturbations. J. Sound Vib.: 314, 526-535.

[23]. Yan, J.J., Hung, M.L., & Liao, T.L. (2006). Adaptive sliding mode control for synchronization of chaotic gyros with fully unknown parameters. J. Sound Vib.: 298, 298-306.

[24]. Fang, J. Q., Hong, Y., & Chen, G. (1999). Switching manifold approach to chaos synchronization. Phys. Rev. E: 59, R2523-R2526.

[25]. Yin, X., Ren, Y., & Shan, X. (2002). Synchronization of discrete spatiotemporal chaos by using variable structure control. Chaos, Solitons Fractals: 14, 1077-82.

[26]. Yassen, M.T. (2006). Chaos control of chaotic dynamical systems using backstepping design. Chaos, Solitons Fractals: 27, 537-548.

[27]. Yassen, M.T. (2007). Controlling, synchronization and tracking chaotic Liu system using active backstepping design. Phys. Lett. A: 360, 582-587.

[28]. Lu, J., & Zhang, S. (2001). Controlling Chen's chaotic attractor using backstepping design based on parameters identification. Phys. Lett. A. 286, 148-152.

[29]. Wang, C., & Ge, S. S. (2001). Adaptive synchronization of uncertain chaotic systems via backstepping design. Chaos, Solitons Fractals: 12, 1199-206.

[30]. Shahzad, M. (2011). Synchronization Behaviour of the Rotational Dynamics of Enceladus Via Active Control. Higher Education of Nature Science: 1 (1), 1-6.

[31]. Vincent, U. E., & Ucar, A. (2007). Synchronization and anti-synchronization of chaos in permanent magnet reluctance machine. Far East J. Dynamical Systems: 9, 211-221.

[32]. Vincent, U. E., & Laoye, J. A. (2007). Synchronization, anti-synchronization and current transport in non-identical chaotic ratchets. Physica A: 384, 230-240.

[33]. Khan, A., & Shahzad, M. (2008). Control of chaos in the Hamiltonian system of Mimas-Tethys. Astronomical J.: 136, 2201-3.

[34]. Nimeijer, H., & Mareels Ivan, M.Y. (1997). An observer looks at Synchronization, IEEE Trans. Circ. Syst.: 144, 882-890.

[35]. Kim, C.M., Rim, S., Kye, W.H., Ryu, J.W., & Park, Y.J. (2003). Anti-synchronization of chaotic oscillators. Phys. Lett. A: 320, 39-49.

[36]. Emadzadeh, A.A., & Haeri, M. (2005). Anti-synchronization of two different chaotic systems via active control. Trans. Eng. Comp. & Tech.: 6, 62-65.

[37]. Li, C., & Liao, X. (2006). Anti-synchronization of a class of coupled chaotic systems via linear feedback control, Int. J. Bifurc. & Chaos: 16, 1041-7.

[38]. Cai, G., & Zheng, S. (2008). Anti-synchronization in different hyperchaotic systems. Journal of Information & Computing Science: 3, 181-8.

[39]. Shahzad, M. (2011). Synchronization and Anti-synchronization of a Planar Oscillation of Satellite in an Elliptic Orbit via Active Control. Journal of Control Science and Engineering, 2011: 816432.

Full Article (HTML)

Pdf

Research Paper

Analysis of Liver Cancer DNA Sequence data using Latent values

N. Senthil Vel Murugan* , V. Vallinayagam, K. Senthamarai Kannan*

- Department of Mathematics, St.Joseph's College of Engineering, Chennai.

Department of Statistics, Manonmaniam Sundaranar University, Tirunelveli

Murugan, S.V., Vallinayagam, V., and Kannan, K.S. (2012). Analysis of Liver Cancer DNA Sequence Data Using Latent Values. i-manager’s Journal on Mathematics, 1(2), 34-37. https://doi.org/10.26634/jmat.1.2.1850

Abstract

Extraction of meaningful information from large experimental data sets is a key element in bioinformatics research. Recent advances in high-throughput genomic technologies enable acquisition of different types of molecular biological data Orly Alter (2003). Present evidence, based on systematic studies of the entire GenBank database Buldyrev (1998). Statistical approaches help in the determination of significance configurations in Protein and Nucleic acid sequence data Ying Guo (2008). In the last two decades the researchers have drawn much attention about liver cancer. Liver cancer is a disease in which malignant cells form in the tissues of the liver. It is relatively rare form of cancer but has a high mortality rate. The aim of this paper is analyzed the liver cancer DNA sequence data using Latent values and Stationary distributions. The reasonable results verify the validity of our method.

References

[1]. Buldyrev et al. (1998). “Analysis of DNA sequences using methods of statistical physics”, Physica A 249, pg. 430 – 438.

[2]. Bullard et al. (2010). “Evaluation of statistical methods for normalization and differential expression in mRNA-seq experiments”, Bioinformatics.

[3]. Jin Woo Kim et al. (2003). “Gene expression profiling of preneoplastic liver disease and liver cancer: a new era for improved early detection and treatment of these deadly diseases?, carcinogenesis”, Vol.24 no.3, pg. 363 – 369.

[4]. Samuel Karlin et al. (1992). “Chance and Statistical Significance in Protein and DNA sequence analysis”, Science Vol.257.

[5]. Tan Wai-Yuan, (2002). “Stochastic Models with Applications to Genetics, Cancers, Aids and other Biomedical systems”, World Scientific Publishing Co. Ltd.

[6]. Ying Guo et al (2008). “A new method to analyze the similarity of the DNA sequences”, Journal of Molecular structure: THEOCHEM 853, pg. 62 – 67.

i-manager's Journal on Mathematics (JMAT)

Current Issue Vol. 13 Issue 2

Most Read

Most Cited

Volume 1 Issue 2 April - June 2012

S-α Surfaces Of Biharmonic S-Curves According To Sabban Frame In Heisenberg Group Heis3

Talat Körpinar* , Essin TURHAN**

*-** Firat University, Department of Mathematics, Elazig, Turkey.

Körpinar, T., and Turhan, E. (2012). S-? Surfaces Of Biharmonic S-Curves According To Sabban Frame In Heisenberg Group Heis3. i-manager’s Journal on Mathematics, 1(2), 1-6. https://doi.org/10.26634/jmat.1.2.1844

Abstract

References

Full Article (HTML)

Pdf

The Inverse Surfaces Of Tangent Developables With Respect To Sc(r)

Muhittin Evren Aydin* , Mahmut ERGÜT**

*-** Department of Mathematics, Firat University, Turkey.

Aydin, M.E., and Ergüt, M. (2012). The Inverse Surfaces of Tangent Developables with Respect to S ( R). i-manager’s Journal on Mathematics, 1(2), 7-12. https://doi.org/10.26634/jmat.1.2.1846

Abstract

References

Full Article (HTML)

Pdf

On Some New Generalized Difference Sequence Spaces Defined By A Sequence Of Orlicz Functions

Cigdem A. BEKTAS* , Gülcan Atici**

* Department of Mathematics, Firat University, Turkey. ** Department of Mathematics, Mus Alparslan University, Turkey.

Bektaþ, C.A., and Atici, G. (2012). On Some New Generalized Difference Sequence Spaces Defined By A Sequence of Orlicz Functions. i-manager’s Journal on Mathematics, 1(2), 13-19. https://doi.org/10.26634/jmat.1.2.1847

Abstract

References

Full Article (HTML)

Pdf

Non-null Special Curves of AW(k)-type in Minkowski 3-Space

Handan Öztekin* , Sezin Aykurt**

* Department of Mathematics, Faculty of Science, Firat University, Elazig, Turkey. ** Department of Mathematics, Faculty of Science and Art, Ahi Evran University, Kirsehir, Turkey

Öztekin, H., and Aykurt, S. (2012). Non-Null Special Curves of Aw(K)-Type in Minkowski 3-Space. i-manager’s Journal on Mathematics, 1(2), 20-25. https://doi.org/10.26634/jmat.1.2.1848

Abstract

References

Full Article (HTML)

Pdf

Computational Study of Synchronization and Anti-Synchronization In Mimas-Tethys System

Ayub Khan* , 0**

* Associate Professor, Department of Mathematics, Zakir Husain College, University of Delhi, New Delhi, India. ** Assistant Professor, Department of General Requirements, College of Applied Sciences, Nizwa, Oman.

Khan, A., and Shahzad, M. (2012). Computational Study of Synchronization and Anti-Synchronization in Mimas-Tethys System. i-manager’s Journal on Mathematics, 1(2), 26-33. https://doi.org/10.26634/jmat.1.2.1849

Abstract

References

Full Article (HTML)

Pdf

Analysis of Liver Cancer DNA Sequence data using Latent values

N. Senthil Vel Murugan* , V. Vallinayagam**, K. Senthamarai Kannan***

*-** Department of Mathematics, St.Joseph's College of Engineering, Chennai. *** Department of Statistics, Manonmaniam Sundaranar University, Tirunelveli

Murugan, S.V., Vallinayagam, V., and Kannan, K.S. (2012). Analysis of Liver Cancer DNA Sequence Data Using Latent Values. i-manager’s Journal on Mathematics, 1(2), 34-37. https://doi.org/10.26634/jmat.1.2.1850

Abstract

References

Full Article (HTML)

Pdf

S-α Surfaces Of Biharmonic S-Curves According To Sabban Frame In Heisenberg Group Heis³

The Inverse Surfaces Of Tangent Developables With Respect To S_c(r)

* Department of Mathematics, Firat University, Turkey.

** Department of Mathematics, Mus Alparslan University, Turkey.

* Department of Mathematics, Faculty of Science, Firat University, Elazig, Turkey.

** Department of Mathematics, Faculty of Science and Art, Ahi Evran University, Kirsehir, Turkey

* Associate Professor, Department of Mathematics, Zakir Husain College, University of Delhi, New Delhi, India.

** Assistant Professor, Department of General Requirements, College of Applied Sciences, Nizwa, Oman.

N. Senthil Vel Murugan* , V. Vallinayagam, K. Senthamarai Kannan*

- Department of Mathematics, St.Joseph's College of Engineering, Chennai.

Department of Statistics, Manonmaniam Sundaranar University, Tirunelveli