The Multiple Trichotomous Correlation Coefficient [M_Tri] applies the standard coefficient of correlation to a statistically significant Tri-Squared Test as a post hoc measure. It is used in research investigations to determine the multiple correlations that exist through mathematical analysis designed to assess the quality of the relationships that exist between the trichotomous independent and dependent variables. It specifically corresponds to the squared correlation between the actual research derived By values of the dependent variable acquired via the Tri–Squared Triple-I research instrument. It can also be interpreted as the proportion of the variance of the trichotomous dependent variables in deference to the trichotomous independent variables. Due to the design of the Tri-Squared Test, the trichotomous independent variables (as the “Trichotomous Categorical Variables”) have a series of measurable pairwise orthogonal relationships with the trichotomous dependent variables (as the “Trichotomous Outcome Variables”). This is specifically illustrated by the “Standard 3 × 3 Tri–Squared Table”. Intrinsically, the Multiple Trichotomous Correlation Coefficient is equal to the sum of the squared coefficients of correlation between each independent variable and its associated dependent variable (that can be seen in the Standard 3 × 3 Table row outcomes). These relations hold true because all of the variables in the Tri-Squared Test are uniquely orthogonal. Thus, the significance of a multiple coefficient of correlation can be assessed with an M_Tri cumulatively calculated ratio. This uniquely identified trichotomous correlation coefficient is actually the overall squared value that ascertains the overall holistic relationship between all Tri-Squared variables.

The acronym “MULTRICOR” represents “Multiple Trichotomous Correlation (Analysis)”. A calculated MULTRICOR test represents the strength of the many relationships that exist between the independent and dependent variables of a statistically significant Tri-Squared Test. A MULTRICOR test measures the dependent variable as “y” [identified as the Trichotomous Outcome Variables, universally represented by the acronym, “TOV”] in their standard orthogonal ordinate Cartesian Coordinates and establishes the strength of their relationship with the research independent variables as “x” [identified as the Trichotomous Categorical Variables universally represented by the acronym, “TCV”] in their standard orthogonal abscissa Cartesian Coordinates. In terms of the comprehensive post hoc MULTRICOR statistic, the “Multiple Trichotomous Correlation” is taken into account by the cumulative comprehensive MULTRICOR Analysis Calculation represented by the “M_Tri” value. Additionally, MULTRICOR measures the strength of the interrelationships that exist between the TCV and TOV via row calculations conducted on the “Standard 3 × 3 Table” of a statistically significant Tri-Squared Test.

Tri-Square or Tri-Squared comprehensively stands for “The Total Transformative Trichotomous-Squared Test” (or “Trichotomy-Squared ”). The Total Transformative Trichotomous-Squared Test provides a methodology for the transformation of the outcomes from qualitative research into measurable quantitative values that are used to test the validity of hypotheses. It is based on the mathematical “Law of Trichotomy”. In terms of mathematics, Apostol in his book on calculus defined “The Law of Tricohotomy” as: Every real number is negative, 0, or positive. The law is sometimes stated as “For arbitrary real numbers a and b, exactly one of the relations ab holds” (Apostol, 1967). It is important to note that in mathematics, the law (or axiom) of trichotomy is most commonly the statement that for any (real) numbers x and y, exactly one th of the following relations holds. Until the end of the 19 century, the law of trichotomy was tacitly assumed true without having been thoroughly examined (Singh, 1997). A proof was sought by Logicians and the law was indeed proved to be true. If applied to cardinal numbers, the law of trichotomy is equivalent to the axiom of choice. More generally, a binary relation R on X is trichotomous if for all x and y in X exactly one of xRy, yRx or x = y holds. If such a relation is also transitive it is a strict total order; this is a special case of a strict weak order. For example, in the case of three elements, the relation R given by aRb, aRc, bRc is a strict total order, while the relation R given by the cyclic aRb, bRc, cRa is a non-transitive trichotomous relation. In the definition of an ordered integral domain or ordered field, the law of trichotomy is usually taken as more foundational than the law of total order, with y = 0, where 0 is the zero of the integral domain or field. In set theory, trichotomy is most commonly defined as a property that a binary relation < has when all its members < x,y > satisfy exactly one of the relations listed above. Strict inequality is an example of a trichotomous relation in this sense. Trichotomous relations in this sense are irreflexive and antisymmetric (Sensagent, 2012).

The foundational idea of a “Trichotomy” has a detailed long history that is based in discussions surrounding higher cognition, general thought, and descriptions of intellect. Philosopher Immanuel Kant adapted the Thomistic acts of intellect in his trichotomy of higher cognition as: (a) understanding; (b) judgment; and (c) reason; which he correlated with his adaptation in the soul's capacities as - (d) cognitive faculties; (e) feeling of pleasure or displeasure; and (f) faculty of desire (Kant, 2007). The Total Transformative Trichotomous-Squared Test provides a methodology for the transformation of the outcomes from qualitative research into measurable quantitative values that are used to test the validity of hypotheses. The advantage of this research procedure is that it is a comprehensive holistic testing methodology that is designed to be a static way of holistically measuring categorical variables directly applicable to educational and social behavioral environments where the established methods of pure experimental designs are easily violated. The unchanging base of the Tri-Squared Test is the 3 × 3 Table based on Trichotomous Categorical Variables and Trichotomous Outcome Variables. The emphasis the three distinctive variables provide a thorough rigorous robustness to the test that yields enough outcomes to determine if differences truly exist in the environment in which the research takes place (Osler, 2013a).

Tri-Squared is grounded in the combination of the application of the research two mathematical pioneers and the author's research in the basic two dimensional foundational approaches that ground further explorations into a three dimensional Instructional Design. The aforementioned research includes the original dissertation of optical pioneer Ernst Abbe who derived the distribution that would later become known as the chi square distribution and the original research of mathematician Auguste Bravais who pioneered the initial mathematical formula for correlation in his research on observational errors. The Tri-Squared research procedure uses an innovative series of mathematical formulae that do the following as a comprehensive whole: (1) Convert qualitative data into quantitative data; (2) Analyze inputted trichotomous qualitative outcomes; (3) Transform inputted trichotomous qualitative outcomes into outputted quantitative outcomes; and (4) Create a standalone distribution for the analysis possible outcomes and to establish an effective-research effect size and sample size with an associated alpha level to test the validity of an established research hypothesis. The process of designing instruments for the purposes of assessment and evaluation is called “Psychometrics”. Psychometrics is broadly defined as the science of psychological assessment (Rust & Golombok, 1989). The Tri-Squared Test pioneered by the author, factors into the research design a unique eventbased “Inventive Investigative Instrument”. This is the core of the Trichotomous-Squared Test. The entire procedure is grounded in the qualitative outcomes that are inputted as Trichotomous Categorical Variables based on the Inventive Investigative Instrument (Osler, 2013c). Osler (2012a) initially defined the Tri-Squared mathematical formula in the Journal on Mathematics article entitled, “Trichotomy- Squared - A novel mixed methods test and research procedure designed to analyze, transform, and compare qualitative and quantitative data for education scientists who are administrators, practitioners, teachers, and technologists” as follows:

(1)

The Tri-Squared distribution is a static mathematical extraction out of the Chi Square distribution. This test is not the only test based on the Chi Square distribution (as it is a mathematical distribution that is frequently used directly or indirectly in many tests of significance). Similar to the Chi Square distribution, the Tri–Squared distribution has the following characteristics: (1) It has only a single parameter (the distribution Degrees of Freedom written as “d.f.”); (2) The entire distribution is positively skewed; and (3) The Degrees of Freedom are mathematically written,“[C-1] [R- 1]” which is equal to the distribution mean. Unlike, the Chi Square distribution, the Tri-Squared distribution has the following characteristics: (1) The distribution Degrees of Freedom never changes, therefore, it never approaches the Normal Gaussian Distribution (the bell curve); (2) As a static test the Tri-Squared Degrees of Freedom is always [C- 1] [R-1] = [3 – 1][3 –1] = [2][2] = 4 = the distribution mean; (3) The distribution mode is always [d.f.– 2] = [4 – 2] = 2; (4) The distribution median is always approximates [d.f. – 0.7] = [4 – 0.7] = 3.3; (5) Due to the static or unchanging nature of the distribution, the distribution skew is always positive with the d.f. always equaling 4; and (6) The distribution formulae uses brackets “[ ]” in its formulaic notations to emphasize “a concentration on” for purposes of clarity. The Tri-Squared distribution is the foundation for the Tri-Squared Test, which comprehensively incorporates the following Tri-Squared formulae: The Calculated Column Standard Deviation, The Calculated Row Standard Deviation, and The Sample Effect Size. The Tri-Squared Test is designed to create a comprehensive holistic research methodology from calculations conducted on the Standard 3 × 3 Tri-Squared Table which produces the following: (1) A positive result; (2) No information on the variable relationship direction; and (3) Associated Effect Size, Sample Size, and Alpha Levels (Osler & Waden, 2012b). It is important to note that the research instrument used in Tri-Squared is an invariant (unchanging) fixed static Test.

The Table that follows lists the relative strength of relationship between MULTRICOR TCV and TOV based upon specific intervals. These final MULTRICOR outcomes are described and defined so that the research investigator can accurately describe the type and individual strength of overall relationship [as “m_Tri”] and in between interrelationships [as “Multri_{[interR1- 3]}". The research report will refer to this Table as the definitive descriptive for all MULTRICOR research.

The data from the initial significant study was made into trichotomous or “trivariate” through the grouping of the initial research instrument questions into the following three Trichotomous Categorical Variables: a₁= Successful via: Impact, and Positive Testing [the summation of the outcomes of the assessment instrument item 1]; a₂ = Made  a Difference via: Participation, and Graduation Rate [the summation of the outcomes of the assessment instrument item 2]; and a₃ = Aided in Retention via: Drop Out Rate, and  Attendance [the summation of the outcomes of the assessment instrument item 3]. The Standard Tri-Squared 3 × 3 Table has the following Trichotomous Outcome Variables: b₁ = Yes; b₂ = No; and b₃ =Unknown. The Tri-Squared Statistical model was used to analyze data to determine the attitudes and perceptions of faculty as leaders. The quantitative mathematical application of the Trichotomous-Squared (“Trichotomy-Squared”, “Tri- Squared” or “Tri-Square”) statistical analysis procedure  (Osler, 2012a) had the following results: Tri² Calculated Tri- Squared = [0.581] + [0] + [0.581] + [0.760] + [0.030] + [0.482] + [2.561] + [0.025] + [3.111] = 8.131 (with d.f. = 4 at α = 0.975). For d.f. = 4, the Critical Value for p > 0.975 is 0.484. Thus, we can reject the null hypothesis (H_o) by virtue of the hypothesis test: Tri-Squared Critical Value of 0.484 < 8.131, the Calculated Tri-Squared Value. “Tri-Squared” is the mathematical transformation of qualitative data into quantitative data for the purpose of validating a research hypothesis (clearly illustrated in Table 1). Table 2 illustrates and validates the process of transforming qualitative data into quantitative data as a means of in-depth mixed methods for the purposes of discrete data analysis. The 3 × 3 Table reports the transformed quantitative outcomes based on the Inventive Investigative Instrument Trichotomous Categorical Variables according to participant responses as the Trichotomous Outcome Variables. Table 2 data displays that participants primarily and overwhelmingly selected the “Yes” Categorical Variable (a₁b₁ = 48, a₂b₁ = 43, and a₃b₁ = 38) rather than the alternative Categorical Variables of either “No” or “Unknown” (the “Unknown” C. V. indicated unselected or inapplicable responses to an item). The mathematical formula for the Tri-Squared is reported illustrating the final outcome of the research hypothesis test: the null hypothesis (H ) is rejected at p > 0.975 is 0.484 because 0 the Tri-Squared Test Critical Value of 0.484 < 8.131, the Calculated Tri-Squared Test Value. Many statistical measures used in education are based on experimental research designs that require scientific methodologies and cannot be implemented in educational institutions without violating legal policies or severely disturbing the learning environment associated instructional climate (Osler, 2012b). To promote the previously mentioned efforts towards empowering faculty in the areas of social justice, empowerment, and environmental equity, novel statistical measures and methods are required that are specifically designed for education and educational environmental needs. The Tri-Squared statistical model provides scientific subsequent measures based on rigor and grounded in the foundation of long standing educational research, fundamental educational theory, and innovations in qualitative, quantitative, and mixed methods research designs native to the specifics of pedagogy and andragogy (Osler, 2013b).

Table 1. MULTRICOR: Strength of Multiple Trichotomous Correlation and Interrelation Table = Multri_{[interR1- 3]} and m_Tri

Table 2. The Initial Outcomes of the Sample Tri–Squared Test

The MULTRICOR final calculated value [represented by “m_Tri”] for the sample post hoc advanced research investigation analysis (using the sample data) is follows:

(2)

where, m_Tri = A positive or negative calculated value between 0.00 and 1.00.

The Tri-Squared Test statistical analysis procedure was used to analyze and validate the initial data outcomes that were a result of the initial study (Osler, 2012b). An alpha-level of 0.975 was considered in light of the research context that was evidence-based in the prescribed schools that had restricted and controlled learning environments that allowed for very few chance factors to affect the outcomes of the research investigation (n_Tri = 17 with 17 × 3 = 51 items per the outcomes of the Trichotomous Variables on the Inventive Investigative Instrument: The Osler-Waden 9^th Grade Academies, Centers, and Center Models Assessment Instrument©). This was coupled with the data gathered from administrators that allowed for minimal chance factors to affect research outcomes. The 0.975 estimate was reasonable for this particular study based on the calculated Tri-Squared Effect Size. In addition, due to the exploratory context and nature of the research investigation (in an area where little previous research has been done regarding gender, ethnicity, and education administration leadership) a less stringent level of significance of 0.975 was the best fit for the research study. The study yielded the following final results using the Tri- Squared Test in the standard Tri-Squared 3 × 3 tabular format (on the following “Sample Research Results: Outcomes of the Sample Tri-Squared Test”). Table 2 that follows begins the step by step procedures for conducting an in-depth MULTRICOR analysis. Table 2 also provides the initial outcomes of the Tri-Squared Test followed by the specific research outcomes provided in the Table 2 narrative that proceeds immediately after the tabular results.

Data Analyzed Using the Trichotomous-Squared Three by Three Table designed to analyze the research questions from an Inventive Investigative Instrument with the following Trichotomous Categorical Variables: a₁ = Successful via:  Impact, and Positive Testing [the summation of the outcomes of the assessment instrument item 1]; a₂ = Made  a Difference via: Participation, and Graduation Rate [the summation of the outcomes of the assessment instrument item 2]; and a₃ = Aided in Retention via: Drop Out Rate, and  Attendance [the summation of the outcomes of the assessment instrument item 3]. The 3 × 3 Table has the following Trichotomous Outcome Variables: b₁ = Yes; b₂ = No; and b₃ = Unknown. The Inputted Qualitative Outcomes  are reported as follows:

The Tri–Square Test Formula for the Transformation of Trichotomous Qualitative Outcomes into Trichotomous Quantitative Outcomes to Determine the Validity of the Research Hypothesis:

(3)

(4)

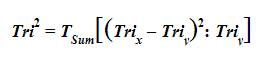
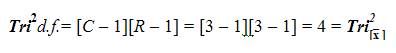
Table 1 illustrates the qualitative mathematical application of the Trichotomous-Squared (“Trichotomy-Squared”, “Tri- Squared” or “Tri-Square”)statistical analysis procedure. The  results are:Tri² Critical Value Table = 8.131 (with d.f. = 4 at α = 0.975). For d.f. = 4, the Critical Value for p > 0.975 is 0.484. The calculated Tri-Square value is 8.131, thus, the null hypothesis (H_o) is rejected by virtue of the hypothesis test  which yields the following: Tri-Squared Critical Value of 0.484 < 8.131, the Calculated Tri-Squared Value. In Table 1, the 3 × 3 Table reports the qualitative outcomes based on the Inventive Investigative Instrument Trichotomous Categorical Variables according to participant responses as the Trichotomous Outcome Variables. Table 1 shows that participants primarily and overwhelmingly selected the “Yes” Categorical Variable (a₁b₁ = 48, a₂b₁ = 43, and a₃b₁ = 38) rather than the alternative Categorical Variables of either “No” or “Unknown” (the “Unknown” C. V. indicated unselected or inapplicable responses to an item). The mathematical formula for the Tri-Squared is reported illustrating the final outcome of the research hypothesis test: the null hypothesis (H_o) is rejected at p > 0.975 is 0.484. 0 Table 3 follows and provides the outputted quantitative outcomes of the Tri-Squared Test and the computational calculations necessary to conduct the initial nine measurement calculations that must be conducted sequentially during the MULTRICOR analysis.

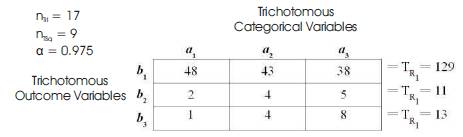
Table 3. The Sample Tri-Squared Test MULTRICOR Equations and Calculations

The mathematical measurements of the MULTRICOR follow with step by step sequential format:

Measurement 1: The Tri-Squared Standard 3 × 3 Table is under Trivariate Analysis, thus: n_R[1-3] = 3 and n_TSq = 9. The Calculated Sum of Trichotomous Outcome Variable Tri- Squared Row Scores are respectively:

b₁ = T²_R1=5597; b^₂ = T²_R2 = 45; and b₃ = T²_R3= 81,

Measurement 2: Tri²_columns= The number of 3 × 3 Standard Tri Squared Table Rows = 3 and Tri²_Rows   -1=3-1=2;

Measurement 3: Tri²_Ext =Tri-Squared External Row Comparisons

= 1006.22

Measurement 4: S²_TR1 = The Variance of T_R1 =The Variance of 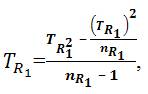where, T_R²₁= The Sum of Squares of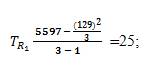  

S²_TR2= The variance of 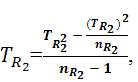, where, T_R²₂ = The Sum of Squares of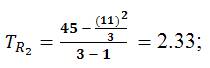  

S²_TR3= The Variance of 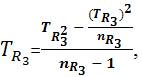, where T_R²₃ = The Sum of Squares of 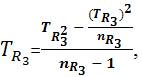=12.33.

Measurement 5: Tri² _Int = Tri-Squared Internal Row Comparisons

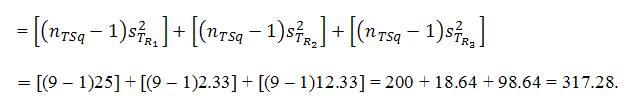
Measurement 6: S_TR1 = The Standard Deviation of S_TR1 = T_R1==5;

S_TR2 = The Standard Deviation of S_TR1=T _R2 = 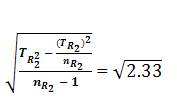=1.526; and

S_TR3 = The Standard Deviation of S_TR3 = T_R3 = 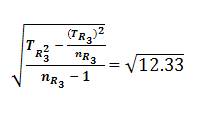= 3.511

Measurement 7: The overall MULTRICOR calculation is as follows:

Multri_[r] =   = Multri_[r]=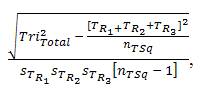

Thus in the example the data for this calculation is inputted in the following manner:

Multri_[r] = Multri_[r] =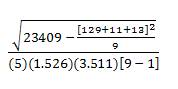

= 0.671 ≈ 0.67.

Measurement 8: The “Multiple Trichotomous Correlation Analysis” final calculated value is represented by the m_Tri  final value. The m_Tri is calculated using the following equation:

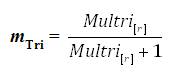
The sample data yielded the following final MULTRICOR calculated value:

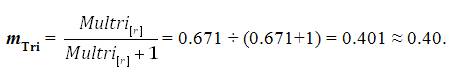
This final m_Tri final value on the “MULTRICOR: Strength of  Trichotomous Correlation and Interrelations Table = Multri _[interR1-3] and m_Tri” (see Table 1) at interval [0.36 to 0.40]  indicates a “Moderately Positive Relationship” (which is the fourth highest Multiple Trichotomous Correlation interval on the entire MULTRICOR Table).

Measurement 9: The MULTRICOR calculation for each of the Trichotomous Outcome Variables [TOV] to determine the overall strength of the interrelationships between Trichotomous Categorical Variables [TCV] and Trichotomous Outcome Variables [TOV] by Tri–Squared 3 × 3 Table Row is as follows:

Multri_[interR1] for [TOV₁ ] = 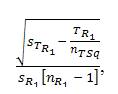,which is calculated in the example provided as = 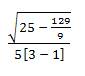= 0.326 (rounded) [“approximately equal to”] ≈ 0.35 which indicates on the “MULTRICOR: Strength of Trichotomous Correlation and Interrelations Table = Multri_[r] and Multri_[r] ” (see Table 1) at interval [.31 to .35] which indicates a “Mildly Positive Relationship” (which is the fifth highest Multiple Trichotomous Correlation interval on the entire Table).

Multri_[interR2] for [TOV₂ ] = 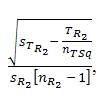,which is calculated in the example provided as 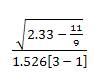=0.345 (rounded) [“approximately equal to”] ≈ 0.40 which indicates on the “MULTRICOR: Strength of Trichotomous Correlation and Interrelations Table = Multri_[r] and Multri_[r] ” (see Table 1) at interval [.36 to .40] which indicates a “Moderately Positive Relationship” (which is the fourth highest Multiple Trichotomous Correlation interval on the entire Table).

Multri_[interR3] for [TOV₃ ] = 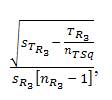,which is calculated in the example provided as = 0.469 (rounded) [“approximately equal to”] ≈ 0.50 which indicates on the “MULTRICOR: Strength of Trichotomous Correlation and Interrelations Table = Multri_[r] and Multri_[r]”  (see Table 1) at interval [.41 to .50] which indicates a “Very Positive Relationship” (which is the third highest Multiple Trichotomous Correlation interval on the entire Table). The “Standard 3 × 3 Tri-Squared Tables” that displays the aforementioned MULTRICOR calculated values for the Sample data is provided in the next section in Table 4 which provides in careful descriptive detail of the overall MULTRICOR results in 3 by 3 tabular format. This is immediately followed by Table 5 which provides the definitions of the MULTRICOR results taken from the “Table 1: MULTRICOR: Strength of Multiple Trichotomous Correlation and Interrelation Table”and transferred to an explicative 3 by 3 trichotomous table that thereby defines the Table 4 data on an overall table of definitive MULTRICOR results and the final MULTRICOR result (Table 5 is ideal for presentations that need to report and further explain the outcomes of a completed MULTRICOR test).

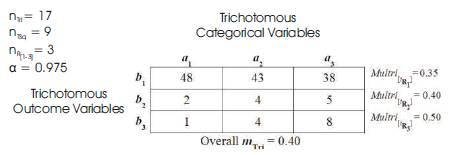
Table 4. Sample Tri-Squared Standard 3 × 3 MULTRICOR Results Table

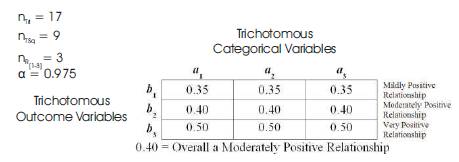
Table 5. Sample Tri–Squared Standard 3 × 3 MULTRICOR Outcome Table

Measurement 10: The Tri–Squared MULTRICOR results in Tabular format

Measurement 11: The Final MULTRICOR Test results in final Multiple Trichotomous Correlation Coefficient format.

The MULTRICOR final calculated value [represented by “m_Tri”] for the sample post hoc advanced research investigation analysis (using the sample data) is follows:

m_Tri = - m_Tri <0> + m_Tri ;

where, m_Tri = 0.40.

The outcomes of the sample data yielded an overall Multiple Trichotomous Correlation of 0.40 thereby indicating that there is an overall “Moderately Positive Relationship” between the Trichotomous Outcome Variables [TOV] and the Trichotomous Categorical Variables. Table 6 reports the operations and procedures for MULTRICOR post hoc testing with massive amounts of data. Table 7 reports the “Sample Tri–Squared Standard 3 × 3 MULTRICOR Results Table for Large Data” similar to Table 4 and Table 8 reports the final overall outcome of the large data MULTRICOR analysis similar to Table 5.

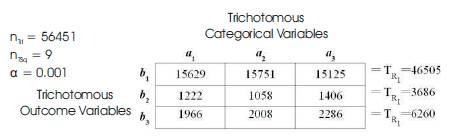
Table 6. Calculations of the Sample Tri-Squared Test for MULTRICOR

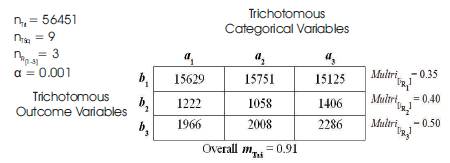
Table 7. Sample Tri-Squared Standard 3 × 3 MULTRICOR Results Table for Large Data

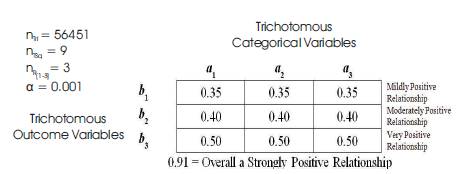
Table 8. Sample Tri–Squared Standard 3 × 3 MULTRICOR Outcome Table

Conducting the Sample Post Hoc MULTRICOR Analysis on the Initially Significant Tri-Squared Research Results where n_Tri is large [such as in this example where n_Tri = 56451] (see Table 6). The equations for conducting this type of MULTRICOR calculation follow in sequential order.

The mathematical measurements of the MULTRICOR follow in step by step sequential format:

Measurement 1: The Tri-Squared Standard 3 × 3 Table is under Trivariate Analysis, thus: n_R[1-3] = 3 and n_TSq = 9. The Calculated Sum of Trichotomous Outcome Variable Tri-Squared Row Scores are respectively: b₁ =T²_R1 = 721125267; b₂ =T²_R2 = 4589484; and b₃ =T²_R3 = 13123016.

Measurement 2: Tri²_Columns = The number of 3 × 3 Standard  Tri–Squared Table Rows = 3 and Tri²_Rows -1=3-1=2.

Measurement 3: Tri²_Ext = Tri-Squared External Row Ext Comparisons

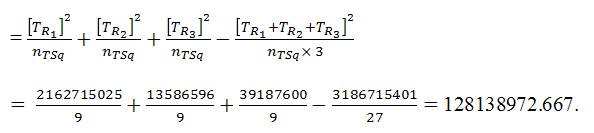
Measurement 4: S²_TR1 = The variance of T_R1 = 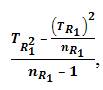, Where, T_R²1 = The sum of squares of T_R1= 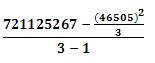= 110129.3333333333;

S²_TR2= The variance of T_R2 = 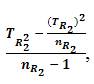Where, T_R²2 = The sum of squares of T_R2= 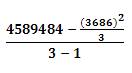= 30309.3333333333;

S²_TR3=The variance of T_R3= 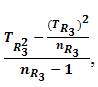Where, T_R²3 = The sum of squares of T_R3= 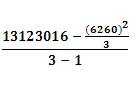= 30241.3333333333;

Measurement 5: Tri²_Int= Tri-Squared Internal Row Comparisons

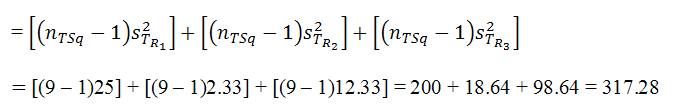
Measurement 6: S_TR1= The Standard Deviation of S_TR1= T_R1= = 331.857; S_TR2= The Standard Deviation of S_TR2=T_R2= = 87.048; and S_TR3= The Standard Deviation of S_TR3=T_R2= =173.900

Measurement 7: The overall MULTRICOR large calculation is as follows:

Multri_[r]=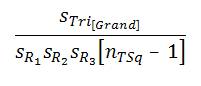= Multri_[r]=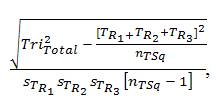

= 9.573894187

Measurement 8: The “Multiple Trichotomous Correlation Analysis” final calculated value is represented by the m_Tri final value. The m_Tri is calculated using the following equation:

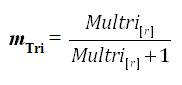
The sample data yielded the following final MULTRICOR calculated value:

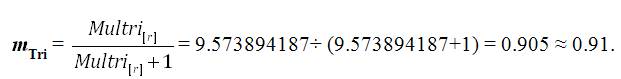
This final m_Tri final value on the “MULTRICOR: Strength of  Trichotomous Correlation and Interrelations Table = Multri_{[interR1-3] ]} and m_Tri” (see Table 1) at interval [0.51 to 0.99]  indicates a “Strong Positive Relationship” (which is the second highest Multiple Trichotomous Correlation interval on the entire MULTRICOR Table).

Measurement 9: The MULTRICOR calculation for each of the Trichotomous Outcome Variables [TOV] to determine the overall strength of the interrelationships between Trichotomous Categorical Variables [TCV] and Trichotomous Outcome Variables [TOV] by Tri–Squared 3 × 3 Table Row is as follows:

Multri_[iR1] for [TOV₁] =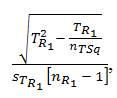 , which is calculated in the example provided as = 40.4597152475 (rounded) [“approximately equal to”] ≈ 0.35 which indicates on the “MULTRICOR: Strength of Trichotomous Correlation and Interrelations Table = Multri_[r] and Multri_[r]” (see Table 1) at interval [.31 to .35] which indicates a “Mildly Positive Relationship” (which is the fifth highest Multiple Trichotomous Correlation interval on the entire Table). 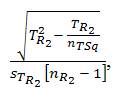Multri_{[iR2 ]} for [TOV₂] = , which is calculated in the example provided as = 12.254 (rounded) [“approximately equal to”] ≈ 0.40 which indicates on the “MULTRICOR: Strength of Trichotomous Correlation and Interrelations Table = Multri_[r] and Multri_[r]” (see Table 1) at interval [.36 to .40] which indicates a “Moderately Positive Relationship” (which is the fourth highest Multiple Trichotomous Correlation interval on the entire Table).

Multri_[iR3] for [TOV₃] =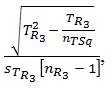 , which is calculated in the example provided as 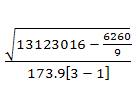= 10.415 (rounded) [“approximately equal to”] ≈ 0.50 which indicates on the “MULTRICOR: Strength of Trichotomous Correlation and Interrelations Table = Multri_[r] and Multri_[r]” (see Table 1) at interval [.41 to .50] which indicates a “Very Positive Relationship” (which is the third highest Multiple Trichotomous Correlation interval on the entire Table). The “Standard 3 × 3 Tri-Squared Tables” that displays the aforementioned MULTRICOR calculated values for the sample data is provided in the next section via Table 7.

Measurement 10: Tri-Squared MULTRICOR results in tabular format.

Measurement 11: The Final MULTRICOR Test results in final Multiple Trichotomous Correlation Coefficient format (for large sample data).

The MULTRICOR final calculated value [represented by “m_Tri”] for the sample post hoc advanced research investigation analysis (using the sample data) is follows:

m_Tri = - m_tri <0> + m_Tri ;

where, m_Tri = 0.91.

The outcomes of the sample data yielded an overall Multiple Trichotomous Correlation of 0.91 thereby indicating that there is an overall “Strongly Positive Relationship” between the Trichotomous Outcome Variables [TOV] and the Trichotomous Categorical Variables.

A Summative Assessment of the Results of the Tri–Squared Advanced Statistical Post Hoc MULTRICOR Test Methodology is given below.

The purpose of this narrative was to chronicle the applicability and epistemological rationale for the MULTRICOR advanced statistical post hoc testing methodology. As illustrated in both small and large data examples Multiple Trichotomous Correlation Analysis is a meticulously valid way of determining the multiple strength of relationships between the variables of the initial research outcomes of a significant Tri–Squared Test. To exhibit its utility, MULTRICOR as an advanced statistical metric was used as a post hoc follow–up to the research analysis as an advanced triostatistical measure to determine the strength of the interrelationships between the Trichotomous Categorical and Outcome Variables. In addition, MULTRICOR provided the overall strength of the relationship of the orthogonal “Standard 3 × 3 Tri–Squared Tables” of two distinct and unique bodies of data. This thereby verified and confirmed that the statistic has multiple use with any size data set. Thus, establishing that MULTRICOR is a very efficient and effective form of a posteriori post hoc analysis of the Tri–Squared Test methodology. This thereby adds much greater breadth and depth to future Tri–Squared research investigations from an in–depth advanced statistical analytical perspective. MULTRICOR sheds much light on the inner workings of the Tri–Squared Test, the Trichotomous Research Models, and Advanced Post Hoc Tri–Squared Testing Metrics, providing an extensive and exhaustive amount of enriching value to the field of “Trichotomous–based Research”. As Tri-Squared research continues to be adopted and grow, tools such as MULTRICOR add value to innovative research in a variety of disciplines and fields.