Due to the current development of Multispectral sensor technology, the use of Multispectral images has become more and more popular in recent years in remote sensing applications. This paper exploits the spectral and spatial redundancies that exist in different bands of multispectral images and effectively compresses these redundancies by means of a lossy compression method while preserving the crucial and vital spectral information of objects that prevails in the multispectral bands. In this paper, interpolated super resolution transform based DWT with Improved SPIHT algorithm for various multispectral datasets has been proposed. The proposed algorithm, a lossy multispectral image compression method yields better performance results for PSNR and Compression Ratio with sym8 wavelet when compared with previous well-known compression methods and existing discrete wavelets.
Depending upon the exploitation of spatial and spectral redundancies that exist in multispectral images in the visible light spectrum is divided into more than three frequency bands and records each of these bands as a separate set of monochrome images. Sensor arrays to capture these bands require a large number of mechanical and optical parts which effectively increases the size and cost of the cameras. A single image band in multispectral images may occupy hundreds of megabytes for storage and moreover the transmission bandwidth to transmit these multispectral images require huge bandwidth for remote sensing applications. In order to mitigate these problems, there is a need for multispectral image compression. The simplest method is to decompose the given multispectral images into different band images, and then to compress these band images using the conventional image compression methods. The multispectral image compression as with monochrome image compression, falls into two categories given by lossy and lossless compression [15]. The decoded image in lossless compression is identical to By the original image with perfect fidelity, but limits the achievable compression ratio. Whereas, lossy image compression attempts to minimize the degradation in output image quality for a given compression ratio. For a given distortion, the rate distortion gives the minimum bit rates and hence maximum compression. Therefore, a lowcomplexity compression codec with high performance is necessary for a multi spectral imagery. The previous methodologies are mainly dealt with the Differential Pulse Code Modulation (DPCM), direct vector quantization, or dimensionality reduction through Principal Component Analysis (PCA) [1] [2] [3] for various multispectral image compressions. This paper, propose a new algorithm for lossy multispectral image compression based on DWT with modified SPIHT encoding and super resolution technique which provides better image quality in terms of high PSNR and compression ratio when compared to other compression methods. For performance evaluation, the authors have investigated several standard lossy compression algorithms for multispectral image compression and compared their performance with the proposed method. The compared algorithms include DCT KLT [7] and DWT SPIHT [2] algorithms. Section 1 explains the need and classification of image compression in the multispectral images. Sections 2 and 3 explain the aim and objectives of the research work. Section 4 explains the proposed super resolution ISPIHT compression technique algorithm for multispectral image compression. The Results and Discussions which are obtained from various multispectral images of various data sets and inbuilt matlab multispectral images, when compared with the existing standard compression methods like DCT KLT [11], and DWT SPIHT [10] in terms of MSE, PSNR, CR, SSIM, and BER are explained in Section 5. Conclusion and the present perspectives are given in the last section.
In order to store or transmit an image data in a more efficient form, redundancies are reduced by means of translating the image data into a more compact form by means of image compression. Uncompressed image data are large in file size and in order to store or retrieve/transmit this uncompressed image, it requires a considerable storage capacity and a retrievable time/transmission bandwidth. In Multispectral images, there are mainly two types of redundancy. Spatial Redundancy and Spectral Redundancy. The correlation which exists between the neighbouring pixels is called as Spatial Redundancy. This is the redundancy which occurs due to self-similarity or patterning within an image. Spectral Redundancy is the redundancy which occurs between different color planes or spectral bands because of their correlation [4-6].
New multispectral instruments generate very high data rates due to the increased spatial and spectral resolutions and they are more expensive due to their high resolution and acquisition capability. Separate sensor array for each band of the EM spectrum has hundreds of megabytes and requires a high capacity storage. The lossless compression does not provide a sufficient degree of data volume reduction to meet the bandwidth requirements of the downlink channel. Thus, there is a need to reduce the number of sensor arrays which captures only maximum entropy decorrelated spectral bands.
The spectral bands in the multispectral images have a lot of intra band and inter band redundancies which can be effectively exploited to compress these images to a large extent for remote sensing applications. To accurately predict the perceived color of a physical surface, know the reflectance of the surface as a function of wavelength and by reducing the spatial, spectral and psycho-visual redundancy among these spectral bands can represent the image with few spectral bands.
The proposed methodology follow the transformed based approach, wherein the transformed representative spectral bands which are largely uncorrelated and having maximum entropy are selected. These bands are then transformed by DWT using symlet 8 wavelet which has maximum symmetry and encoded using an Improved SPIHT algorithm. The image resolution of the compressed image is increased by interpolation Super Resolution methods to have a better PSNR value.
In this work, the first step is to enhance the original multispectral image by means of interpolation based super resolution technique and in the second step, the enhanced multispectral image is subjected to the Discrete Wavelet Transform and symlet 8 dwt is applied on the various bands of the multispectral images, which are then encoded by improved SPIHT algorithm. The spectral and spatial correlation that exists in wavelet coefficients of multispectral images are exploited while encoding with the ISPIHT algorithm. This scheme exploits the spatial and the spectral correlation in the biorthogonal multispectral image subclasses. The proposed technique consists of two steps. First of all, the various bands of multispectral images are analyzed independently using two-dimensional symlet 8 Discrete Wavelet Transform which is shown in Figure 1 and then, the wavelet coefficients are quantized and encoded with Improved SPHIT.
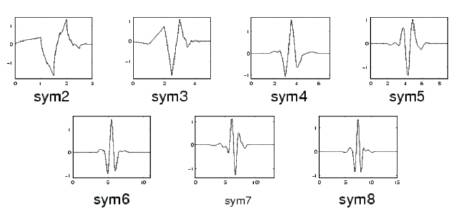
Figure 1. Symlet Wavelets
Figure 2. Illustration of Gradient Degradation. (a) Gradient Field of HR Image (b) Gradient Field of Corresponding LR Image
Super-resolution method obtains a hi-resolution (HR) image from a low-resolution (LR) input as shown in Figures 2 (a) and (b) respectively. There are mainly three classifications for this approach, given as interpolation based methods, reconstruction based methods, and learning based methods. From [8, 9], the image super-resolution approach using a novel generic image prior – gradient profile prior, which is a parametric approach describing the prior shape and the sharpness of the image gradients are given. The assumption of low-resolution imaging process can be modelled as follows:
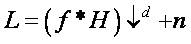
where f denotes a discrete Point Spread Function (PSF), which usually is modelled as a Gaussian filter, H is the reconstructed HR image, * denotes the convolution operator, ↓d is a sub-sampling operator with factor d and n represents the noise that appeared in the LR image.
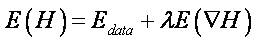
where,
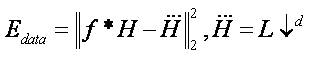
The applications of the wavelet transforms in the image processing domain have been proven to be very useful for various image processing applications like image compression and reconstruction, feature extraction, and image registration [12], [13] , [14]. A two-dimensional scaling function (x, y), and three two-dimensional wavelet functions, φH(x, y), φV(x, y), and φD(x, y), are very much required in two dimensional DWT. These scaling and wavelet functions are a product of two one-dimensional functions. Excluding these functions that produce onedimensional results, given by φ(x) (x), the separable scaling functions are obtained from the remaining four products.
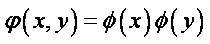
The separable wavelet functions are given by,
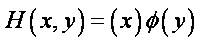
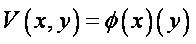
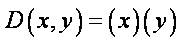
These wavelets measure functional variations, intensity variations for image along different directions, H measures the variations along columns (for example, horizontal edges), the variations along rows (likes vertical edges) are measured by V and the variations along diagonals are measured by D. The multi-resolution representation of a 2-D decomposition image assumes the image space as “separable", i.e. the two axis x and y in the decomposition can be considered independently for the reconstruction of the image. This multi resolution wavelet decomposition is summarized in Figure 3.
Figure 3. Multi-Resolution Wavelet Decomposition
The Multi-Resolution wavelet decomposition algorithm is defined by the following sequence of steps:
1. This decomposition is Started from the image level I0 , level 0 of the multi-resolution sequence (k=0).
2. High-Pass and low-pass filtering of image rows at level k.
3. Decimate by two the number of columns: which results in Lk+1 and Hk+1 .
4. High-Pass and low-pass filtering of image columns at level k.
5. Decimate by two the number of columns: which results in LLk+1, LHk+1, HLk+1, and HHk +1. LLk+1 which is the low/low result, can be renamed as Ik+1, since it performs the compression of the original image at level k+1.
6. The next level of decomposition is set by k, and k+1 continue the iterative process from step (2) to step (5) until the desired level of decomposition is achieved.
The DWT coefficients are used to reconstruct the original image from the above mentioned steps and its reconstruction process is called as the Inverse DWT (IDWT). If C[m,n] represents an image, the DWT and IDWT for C[m,n] may similarly be obtained by separately implementing the DWT and IDWT on each of these dimensions.
The Improved SPIHT algorithm is more dynamic and efficient for encoding the image data when compared to the existing EZW (Embedded Zero Wavelet) [16] [17] algorithm which was presented by Shapiro. The wavelet coefficients are decomposed into significant and insignificant partitions by means of Ian SPIHT algorithm after the application of wavelet transform on an image based on the following function:
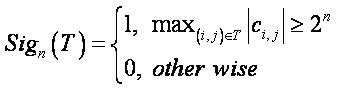
The maximum number of bits required to represent the largest coefficient in the spatial generated bit stream is generated and represented by nmax, which is given as,
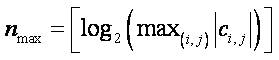
Here Sign(T) is the significance T from a set of coordinates, and cij is the non-zero coefficient value at coordinate (i, j). There are two passes in the multi pass algorithm given by the sorting pass and the refinement pass. The ISPIHT encoding process utilizes three lists LIBT (List of Insignificant Blocks Test) - contains individual coefficients whose magnitudes are smaller than the current thresholds, LIST (List of Insignificant Sets Test) - contains a set of wavelet coefficients that are defined by tree structures and are found to have magnitudes smaller than the current threshold. LSP (List of Significant Pixels), is a list of pixels which are found to have magnitudes larger than the threshold (significant). The multi pass algorithm is performed on the above three lists as shown in Figure 4.
Figure 4. Improved SPIHT Algorithm
1. Initialization Pass for the present threshold.
2. Sorting Pass for the present threshold.
3. Refinement Pass for the present threshold.
4. Quantization-step updates.
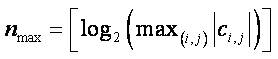where c(i,j) is the Coefficient at
position (i,j) in the image.The LSP contains the coordinates of the pixels that are visited in the refinement pass. For each element (i, j) in LSP, except those included in the last sorting pass (i.e., with the same value of n), output the nth most generated significant bit of | C i, j| is obtained as the output.
The traditional method of performance of lossy compression is determined by simultaneously measuring the number of data operations required to perform the coding processes in terms of MSE, PSNR, CR, BER and SSIM.
The Proposed algorithm was performed using MATLAB 2009b on an INTEL Pentium Core 2 duo (1.8 GHz, 2G RAM). The proposed algorithm is used to test the various multispectral image datasets of different image sizes (balloons 512x512, pompoms 512x512, beers 512x512, strawberries 512x512 and feathers 512x512) of cave multispectral image dataset and inbuilt MatLab multispectral images like LAN file of little coriver and pariscity are considered which contains a 7-band 512-by- 512 Land sat image and a 128-byte header followed by the pixel values, which are Band Interleaved by Line (BIL) in the order of increasing multispectral image band number.
These bands are unsigned 8-bit integers, in little-endian byte order and the Real bands 4,3,2 from the LAN file are captured using the MATLAB (R) function multiband read, according to a two-level wavelet decomposition using biorthogonal filters 9/7 [18]. The input multispectral testing images are shown in Figures 5, 6 and 7. The MatLab results for 0.4 bpp for little coriver image is shown in Figure 8. The result analysis of various testing images for DCT KLT, DWT SPIHT, and DWT ISPIHT for 0.4 bpp is shown in Tables 1, 2 and 3 respectively.
Figure 5. 512X512 Multispectral Feathers, Balloons and Lena Input Images
Figure 6. 512X512 Little Coriver, Pariscity and Pompoms Input Images
Figure 7. 512X512 Multispectral Beers and Strawberries Input Images
Table 1. Result Analysis of DCT KLT Compression Method for 0.4bpp
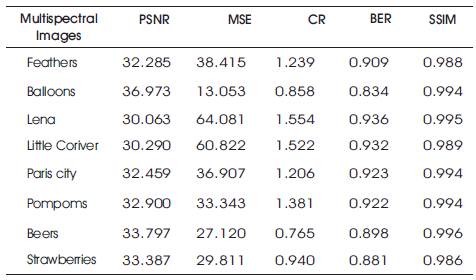
Table 2. Result Analysis of DWT SPIHT Compression Method for 0.4bpp
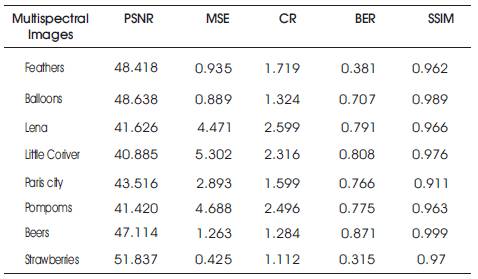
Table 3. Result Analysis of DWT ISPIHT Compression Method for 0.4bpp
Figure 8. MatLab Results for 0.4bpp of the Little Coriver Image
This proposed work introduced a new multi resolution encoding algorithm for multispectral image compression. This algorithm was implemented using a super resolution image technique with 2D-Discrete Wavelet Transform [18]. ISPIHT algorithm is used for optimal bit-allocation to encode the discrete wavelet coefficients. The authors have made an assumption that there exists a spectral correlation in the biorthogonal subclasses. Bands of multispectral data respond differently to DWT and in the wavelet domain which has similar bands are encoded extremely well, which is confirmed by the results obtained by the proposed method when compared to the existing standard image compression techniques like DCT KLT, DWT SPIHT. Future work aims at extending this framework for compressive multispectral imaging.
