De-Noising is a crucial problem for various types of image in the digital image processing. The main objective is to be fade away the noise factor by transfiguring into realistic Image as well as safeguarding the real quality and structure of the Image. Much hardware equipment such as digital electronic devices may suffer some issues that are noisy and blurred images due to degradation in the quality of the visioning image. These noisy images and blur images come under the problem of less information about the working object in a capturing environment. In this paper, the De-Noising technique has been proposed at different standard deviation for each processed image to check that at what level of noise it may work. In this proposed technique, wavelet is applied to a Noisy Image and further on the decomposed sections, SPG-PCA is used for quality enhancement. It consists of two stages: image estimation by removing the noise and further refinement of the first stage. Noise is removed at the maximum extent in first stage and the application of NPG improves the visualization of the De-Noised Image. A different standard deviation helps to optimize the original image which is based on the De-Noising scheme using quality matrices. The proposed technique can also be applied on satellite images, television pictures, medical images, etc. In this research work optimized De-Noising matrices like PSNR, SSIM, Maximum Difference and Normalized Cross-Correlation for the Dataset. Experimental results show a much improved performance of the proposed filters in the presence of Gaussian noise that are analyzed and illustrated.
In the current scenarios, the research and technology are vast areas of digital images, which play a vital role in human's daily life applications-satellite television, magnetic resonance imaging, computer tomography and other related areas of geographical information systems and astronomy. Data sets taken from image devices are generally noisy and follow raw information. Imperfect old instruments, problems with the data acquisition process in sensing information of digital image, and interfering with natural phenomena may give rise to a noisy data, that degrades the data of interest. However, noise can be produced by transmission errors, compression and other natural disaster. So, De-Noising is an important field of research for the quality of digital images and necessary to analyze the taken data from various sources. It becomes more necessary to apply an efficient De- Noising scheme to compensate and enhance the corrupt data. Image De-Noising still remains a challenging issue in the research and scientific field because noise removal introduces artifacts and causes blurring effect of the images. This paper describes various techniques for noise reduction (or De-Noising). Image denoising is still a challenging problem in the fields of image processing and computer vision. It refers to the recovery of a digital image that has been contaminated by some types of noise, e.g., Gaussian noise, or Rician noise, while preserving image features such as the edges and the textures [14]. For this, an algorithmic technique should be more reliable better and estimate the performance of the original image which has taken the data sets and its degraded version should be analyzed in suitable forms. Noise modeling in images is highly affected through capturing instruments, sensing devices, datatransmission media, image quantization and discrete sources of image radiation due to light. An image pixel is described by two quantities, the spatial location and its intensity, while the image local structure is represented as a set of neighboring pixels at different intensity levels. [13],[14], [15].
The aim is to fade away the noise factor by transfiguring the noisy Image into realistic Image as well as safeguarding the real quality and structure of the Image. This motive is not only to remove the noise but also to preserve the structure and edge in the De-Noised image.
The main objective of this research is to propose the new method for image De-Noising and structure preservation using Haar Wavelet and PCA. This method consists of two stages: first stage is image estimation and in the second stage, refinement of the first stage is done.
Different algorithms are used depending on the noise model which follows digitalize and quality images through De-Noising. Most of the natural images have been assumed as additive random noise which is computed as a Gaussian noise, Speckle noise and rician noise. These noises may be observed in the ultrasound images, the MRI images. The scope of the paper concludes and focuses on noise removal techniques for natural images in the geographical research areas. Magnetic Resonance (MR) or CT images are generally corrupted by several artifacts and noise sources [1]. The existing region source of noise in the MR image and CT images are the patient's body. Nowa- days, the body being a conductive medium for the researchers, generates fluctuating fields for each image that will be picked up through the receiver coil [2] the whole measurement chain of the MR scanner (coil, electronics, etc.) has biggest contribution to the noise reduction. Computer aided analysis and visual inspection of the images became impossible due to the presence of noise in MRI. Therefore, de-noising is required for best results. In the early days, many authors applied the conventional classical de-noising techniques to de-noise MRI. These methods assumed the noise in the MRI as Gaussian. The major problem of these techniques is that, the biasing quality effects of Rician noise, which defines to the magnitude MR images, were not taken into account. This bias grows as SNR decreases. Later, many methods were proposed to de-noise the MR images. The most popular family of methods proposed for de-noising MR images are the Non-Local Means (NLM), Partial Differential Equations (PDE), and the Wavelets and Maximum Likelihood (WML) estimation methods. NLM- based methods were proposed in [3-5] for de-noising magnitude of the MR Images. Sijbers et al., [6] and Samsonov & Johnson in [7] proposed the adaptive anisotropic diffusion methods for de-noising MR images. These methods were based on the classical second-order Perona–Malik [8] anisotropic diffusion. However [9], it is mentioned that the anisotropic diffusion methods based on second-order Perona–Malik can cause staircase effects in the filtered images. To reduce this effect, a fourth-order PDE was invented by Lysaker et al. [10], thus main advantage of this method is its capability to compute signals with a little change in the intensity value of the signals. Jyotsna and Sunita [11] used a data likelihood term and combined with Perona–Malik method that was related to anisotropic diffusion to effectively de-noise an MR image. [12] proposed a Linear Minimum Mean Square Error (LMMSE) approach to de-noise the Rician distributed data. Recently, Krissian and Aja-Fernández proposed a noise-driven anisotropic diffusion used as a filter for denoising the MR images. ML-based methods were proposed into de-noise magnitude MR images. This paper propose an wavelet based de-noising technique which will also preserve the structure and various features. It is an edgepreserving De-noising technique. The proposed De-Noising method accounts for various characteristics which is analyzed by using multiple parameters like PSNR, SSIM, MD, NK of the data and also preserves the relevant edge features.
This paper designs the methodology to improve the De- Noising image quality in image processing. Various steps are used such as – Load images from the online database, Add noise to the original image with different deviation (sigma=10, 20, 30), Apply wavelet De-Noising technique using Haar wavelet, Perform SPG and calculate the Euclidean distance between the pixels according to SPG, and Apply PCA according to the NPG [15].
Figure 1 shows various steps in the proposed Methodology of De-noising.
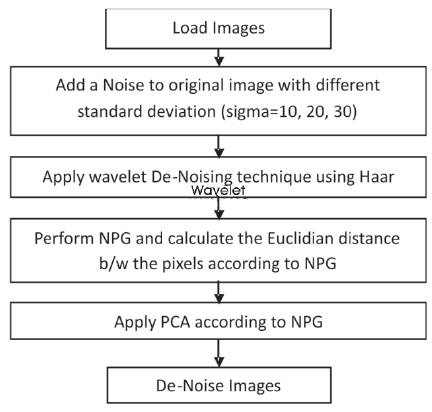
Figure 1. Various Steps used in the Proposed Methodology for De-Noising
It depends on the density function. It is helpful to remove the mimic effects of the House and the images. In the De- Noising process, Gaussian noise is used to check the quality of the De-Noising image. Gaussian noise is also suitable for intrinsic value information of the De-Noising image.
The image with noise is decomposed by Haar wavelet transform to select the soft threshold for removing noise. This transforms wavelet is used to find the threshold value in the De-Noising process. It has been found that the image information is lost using the threshold value from the original De-Noising House image. Haar wavelet transformation is more suitable in the De-Noising process for providing better information about image quality.
LPGs are used to check the location of each pixel in the complete image for the noise reduction algorithm. LPG uses the local window in the original image for the noise removal using the transformation matrix.
PCA is used for the dimension reduction for each original image for better performance in the subspace projection of the working image. It transforms the original database images that are uncorrelated in the PCA domain. It helps to discard all the uncorrelated values from the original image. PCA takes advantage of the eigen vector properties for the determination of selected object orientation. PCA fully decorrelates the original data set, so that the energy of the signal will concentrate on the small subset of the PCA transformed data set. Energy of noise spreads over the whole image. Over PCA the domain signal from noise can be easily distinguished.
In this paper, the authors have found out the results on the basis of previous work and the proposed work. The proposed works have shown better results as compared to the previous work. In this, they have been assuming three matrices for the De-Noising matrices. In this paper, results explain the De-Noising process into four steps following as:
The actual parameter computed is the peak signal-to noise ratio for the reconstructed image, which is called PSNR [15]. Assume that given a original image I₁(m,n) and a De-noised image I₂ (m,n) compute the PSNR using the following as,
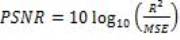
Table 1 shows the comparison of PSNR between the previous work and the proposed work for image De-Noising process. The proposed method has shown better PSNR value for the De-noised Image at various levels of Noise.
Figure 2 shows the Comparative analysis of PSNR in the graphical form.
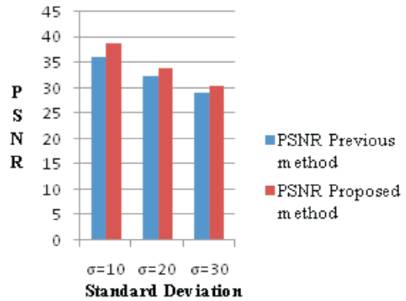
Figure 2. Comparison to PSNR graph for House

Table 1. Comparison of PSNR using House Image
The Structural similarity is used to improve the performance of the peak-signal-to-noise ratio and the mean square error. It is more suitable for the De-Noising the information for the security purposes in future research work [15] .
In Table 2, the comparison to SSIM between the previous work and the proposed work in an image De-Noising process has been shown. The proposed method has shown better SSIM for the De-Noised house image.
Figure 3 shows the comparative analysis of SSIM in the graphical form.
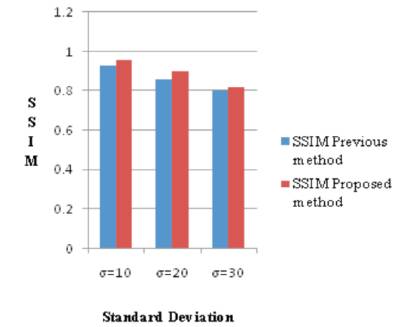
Figure 3. Comparison to SSIM graph for House
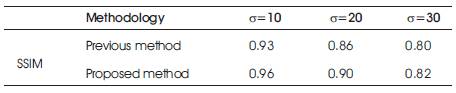
Table 2. Comparison of SSIM using House Image
Maximum difference refers to the pixel intensity for constrast image in De-Noising. It is used for the histogram stretching.
In Table 3 shows the maximum difference found for the house image at different standard deviation values,10, 20, 30. As the value of standard deviation increases the Noise factor, it will be good to have less difference between the original and De-Noised Image.
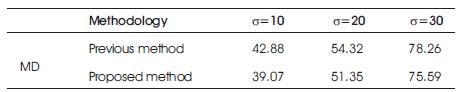
Table 3. Comparison of MD using House Image
Figure 4 shows the comparative analysis of maximum difference in the graphical form.
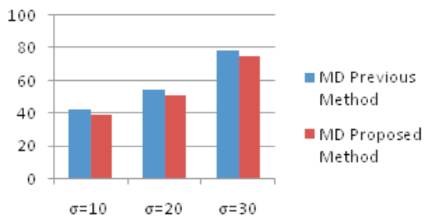
Figure 4. Comparison to Maximum difference graph for House
Normalized Cross-Correlation is used to find the similarity function between two processed images. Table 4 shows the Normalized Cross-Correlation calculated for the correlation matrix. It is used for brightness of the image using different standard deviation.
Figure 5 shows the comparative analysis of normalized cross correlation in the graphical form.
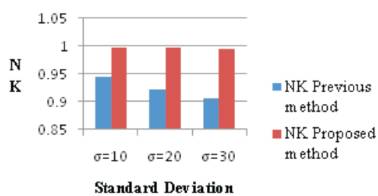
Figure 5. Normalized Cross CorrelationComparison Graph
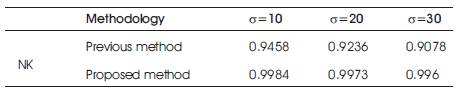
Table 4. Comparison of NK using House
Figures 6 (a-d) show the detailed steps of algorithm. The first Image of this Table is the Original Image. Second Figure shows the Image having Noise Element and it is Degraded. Third Image is the 1st Stage of the Proposed Algorithm. Fourth image shows the 2nd Stage output image which is De-Noised.

Figure 6 (a-d). House Images used in De-Noising
Figures 7 (a-d) show the Histogram of House image as a result of various steps for De-Noising. The Histogram of Original Image and the De-Noised Image is almost same and the similarity can be analyzed using various parameters.
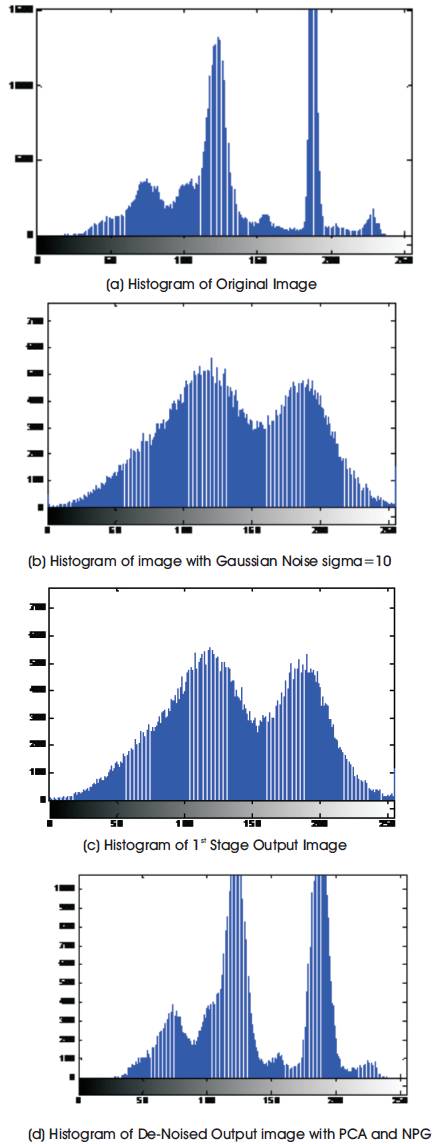
Figure 7 (a-d). Histogram of House Image at various steps of De-Noising
In the above Figure, the histogram of all the steps are used from the House image in a De-Noising process. In this paper, the proposed method shows better histogram output for House images in De-noising.
According to the current proposed research work, the main concentration have been given to the matrices such as PSNR, SSIM, Maximum Difference, and Normalized Cross- Correlation for the De-Noised quality images. The proposed method has aimed at developing a De-Noising method under multiplicative noise and thus Gaussian Noise has been used. The Proposed work provides better visualization and structure preservation of the De-Noised Image. The Visualization is enhanced by improving the brightness and contrast of the processed image. Haar Wavelets have proved to be good for De-Noising of the natural images, because of their energy compactness, sparseness and correlation properties. The value of PSNR is known to be better than the previous method. The value of NK is approximately equal to 1, hence it signifies that the De-Noised Image is equivalent to the original image. Each technique in the field of digital image would be helpful for the further additional processing techniques for better performance and analysis without the loss of information.