With the availability of different medical imaging equipment for diagnoses, medical professionals are increasingly depending on the computer aided techniques for retrieving similar images from large repositories. This work investigates medical image retrieval problem for lossless compressed images. Lossless compression technique is utilized for compressing the medical images for easy transmission and storage. Texture features are extracted using Gabor filters, Shape features using the Gabor - shape and best features of these are selected by using a novel Cuckoo Search algorithm and compared with other statistical techniques. Classification was done by using the Recurrent neural Network. Optimization of the neural network is done using the Cuckoo Search. Experimental results show the advantages of the proposed framework.
Medical image compression plays a key role as hospitals move towards filmless imaging and go completely digital. Image compression will allow Picture Archiving and Communication Systems (PACS) to reduce the file sizes with their storage requirements while maintaining relevant diagnostic information. Lossy compression schemes are not used in medical image compression due to possible loss of useful clinical information and as operations like enhancement may lead to further degradations in the lossy compression. Medical imaging poses the greatest challenge of having compression algorithms that reduce the loss of fidelity as much as possible so as not to contribute to the diagnostic errors and yet have high compression rates for reduced storage and transmission time [1].
Image compression is to reduce irrelevance and redundancy of the image data in order to be able to store or transmit data in an efficient form. Image compression is minimizing the size in bytes of a graphics file without degrading the quality of the image to an unacceptable level [2]. The reduction in file size allows more images to be stored in a given amount of disk or memory space. It also reduces the time required for images to be sent over the Internet or downloaded from Web pages. There are several different ways in which the image files can be compressed. Image compression may be lossy or lossless. Lossless compression is preferred for archival purposes and often for medical imaging, technical drawings, clip art, or comics [3]. This is because lossy compression methods, especially when used at low bit rates, introduce compression artifacts. Lossy methods are especially suitable for natural images such as photographs in applications where minor (sometimes imperceptible) loss of fidelity is acceptable to achieve a substantial reduction in bit rate. The lossy compression that produces imperceptible differences may be called visually lossless [4].
Image compression techniques take advantage of redundancy that occurs. There are different types of redundancy. Each compression methodology will exploit one of these redundancies. The different types of redundancies are spatial, temporal and spectral [5]. The research presented here will focus first on these three types of redundancies although the techniques can be used in the others also. It will make use of spatial redundancies since static spatial X-rays will be used. These are still the most dominant type of medical imaging data used today [6].
Images are retrieved from the database using Content Based Image Retrieval (CBIR), where on presenting a query image, similar images are retrieved. CBIR is advantageous as retrieval is based on the features such as shape, color, and texture of the image. With the huge amount of data stored in the database, CBIR is required for fast retrieval. Yang et al., [7] presented a boosting framework for distance metric learning that aims to preserve both visual and semantic similarities. The boosting framework first learns a binary representation using side information. Syam et al., [8] proposed a CBIR that uses Medical image for retrieval and the feature extraction is used along with color, shape and texture feature extraction to extract the query image from the database medical images. The proposed CBIR technique is evaluated by querying different medical images and the retrieval efficiency is evaluated in the retrieval results.
Han et al., [9] proposed a novel Back Propagation -Based Image Retrieval (BPBIR) system for image retrieval. Bugatti et al., [10] proposed a supervised method for continuous feature selection. The proposed method applies statistical association rules to find patterns relating lowlevel image features to high-level knowledge about the images, and it uses the patterns mined to determine the weight of the features. Experiments showed that the proposed method improves the precision of the query results up to 38%, indicating that statistical association rules can be successfully employed to perform continuous feature selections in medical image databases. Muneesawang [11] explored an unsupervised learning network to include the self-learning capability in image retrieval systems. A Self - Organizing Tree Map (SOTM) to reduce user participation was introduced to automate interactive retrieval, and this is implemented by a novel neural network.
Kumar & Kumaraswamy [12] proposed to implement a novel feature selection mechanism using Discrete Sine Transforms (DST) with Information Gain for reduction. Classification results obtained from the further existing Support Vector Machine (SVM) is compared with the proposed Support Vector Machine model. Results obtained showed that the proposed SVM classifier outperforms the conventional SVM classifier and multilayer perception neural network. Hussain, et al., [13] suggested an efficient technique for MRI brain images involving precise segmentation of normal and pathological tissues. This first process completes the classification through a Fuzzy Inference System (FIS) and FFBNN, where both classifiers use extracted image features as classification input.
Compressed medical image retrieval has not been studied extensively in the literature. In this paper, an investigation has been carried out to retrieve images similar to a query medical image which are compressed for efficient storage and transmission.
In this Proposed work, a study has been done on compressing the image so that it reduces the space required to store and transmits the image easily as it takes less bandwidth. The retrieval of compressed medical images has been studied and a classification algorithm is proposed. Images are compressed using the Daubechies wavelet with Huffman coding and features of these compressed images are extracted using the Gabor shape techniques and the Gabor filters. The feature selection is done using the Information Gain (IG), Mutual Information (MI) and the proposed wrapper based Cuckoo Search (CS) technique. Multi-Layer Perceptron and the proposed Partial Recurrent Neural Network has been used for classification of the compressed Medical images and further the proposed Partial Recurrent Neural Network weights are optimized using the Cuckoo Search for better convergence.
The bandwidth facilities in major towns and villages in India and other developing nations are very less and the available medical staffs and facilities are also poor in rural areas and also in towns areas. This proposed study focus on the retrieval of compressed medical images and also classification of these images, and the better classification method is proposed in this work and it can be utilized in the tele medicine.
In this work, medical images were compressed using Daubechies wavelet with Huffman coding such that visually lossless compression is achieved. The compressed images were segmented and the features extracted using Gabor shape techniques and Gabor filters. Features are selected using Information Gain (IG), Mutual Information (MI) and the proposed wrapper based Cuckoo Search (CS) technique. Multilayer Perceptron and the proposed Recurrent Neural Network (RNN) are used for classification. Figure 1 shows the proposed framework to retrieve medical images. The techniques used are detailed in subsequent subsections.
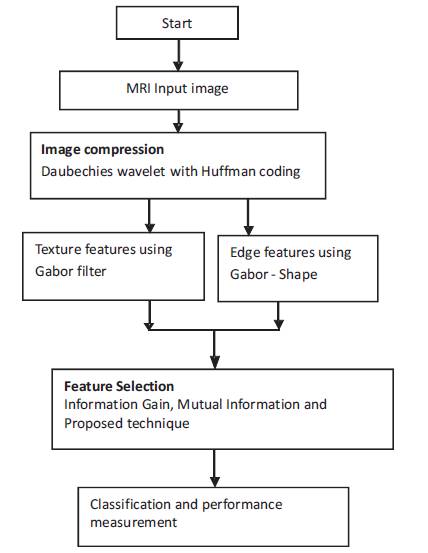
Figure 1. Flowchart of the Proposed Methodology
Daubechies wavelets are a family of orthogonal wavelets defining a discrete wavelet transform and characterized by a maximal number of vanishing moments for some given support [14]. With each wavelet type of this class, there is a scaling function which generates an orthogonal multiresolution analysis [15].
The Huffman code procedure is based on two observations [16].
The Huffman code is designed by merging the lowest probable symbols and this process is repeated until only two probabilities of two compound symbols are left and thus a code tree is generated and Huffman codes are obtained from labelling of the code tree. After the code has been created, coding and/or decoding is accomplished in a simple look-up table manner. The code itself is an instantaneous uniquely decodable block code. It is called a block code, because each source symbol is mapped into a fixed sequence of code symbols. It is instantaneous, because each code word in a string of code symbols can be decoded without referencing the succeeding symbols. It is uniquely decodable, because any string of code symbols can be decoded in only one way. Thus, any string of Huffman encoded symbols can be decoded by examining the individual symbols of the string in a left to right manner.
Step 1: Read the image onto the workspace of the Matlab.
Step 2: Convert the given colour image into a Grey level image.
Step 3: Call a function which will find the symbols (i.e. Pixel value which is non-repeated).
Step 4: Call a function which will calculate the probability of each symbol.
Step 5: Probability of symbols are arranged in decreasing order and lower probabilities are merged and this step is continued until only two probabilities are left and codes are assigned according to the rule that: the highest probable symbol will have a shorter length code.
Step 6: Further Huffman encoding is performed i.e. mapping of the code words to the corresponding symbols will result in a compressed data.
Step 7: The original image is reconstructed i.e. decompression is done using Huffman decoding.
Step 8: Generate a tree equivalent to the encoding tree.
Step 9: Read the input characterwise and left to the table until last element is reached.
Step 10: Output the character encoding in the leaf and return to the root, and continue the step 9 until all the codes of corresponding symbols are known.
Gabor filters are band-pass filters which have both orientation-selective and frequency-selective properties and have optimal joint resolution in both spatial and frequency domains. By applying the properly tuned Gabor filters to a signature image, the texture information can be generated. These accentuated texture information can be used to generate feature vector. Gabor filter has been used successfully in the segmentation of fingerprint and palm prints, as well as their identification [18]. When Gabor filters are applied to each pixel of the image, the dimension of the filtered vector can be very large (proportional to the image dimension). So, it will lead to expensive computation and storage cost. To alleviate such problem and make the algorithm robust, Gabor features are obtained only at the ten extracted fiducial points. If we note C, the number of Gabor filters, at each point will be represented by a vector of C components called ”Jet” [19].
Pseudocodes for Gabor Filter
1. For each frequency f in the frequency flist.
2. For each orientation φ in the orientation flist.
3. Construct a Gabor filter g (f,φ),
4. Convolve g (f,φ) with original image I, get response image R,
5. Compute the mean response in R, denotes as r,
6. Count # of pixels Nr that have a larger value than r,
7. Divide R into n x m frames,
8. For i = 1 to n:
9. For j = 1 to m:
10. Count the # of strong responses Nij and compute the ratio r:
11. r= Nij / Nr;
12. Append r to the feature vector x:
13. Finally,X=[ r1,r 2,....r | flist | * | olist | *n *m]
Gabor filtered output of the image is obtained by the convolution of the image with the Gabor function for each of the orientation as spatial frequency (scale) orientation (Figure 2). Given an image F(x, y), we filter this image Gab (x,y,w,θ,σx,σy) with [20] .
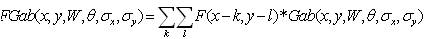
The magnitudes of the Gabor filter responses are represented by three moments.
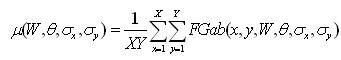
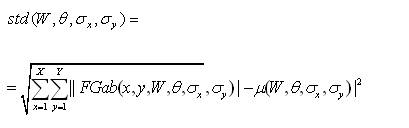
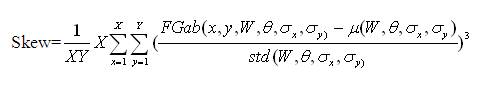
The feature vector is constructed using µ(W, θ, σx, σy), std(W, θ, σx, σy) and Skew as feature components.
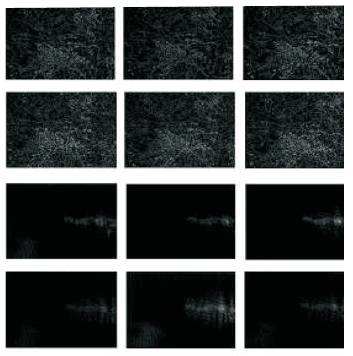
Figure 2. Gabor Output of an Image
The shape descriptors described here [20] computes circularity, aspect ratio, discontinuity angle irregularity, length irregularity, complexity, right-angleness, sharpness, and directedness. Those are translation, rotation (except angle), and scale invariant shape descriptors. It is possible to extract image contours from the detected edges. From the object contour, the shape information is derived. We extract and store a set of shape features from the contour image and for each individual contour. These shapes used are shown in Figure 3. The computation is given by,
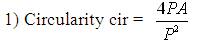
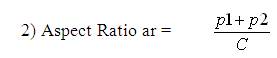
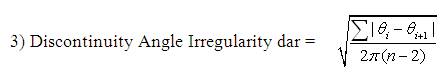
A normalized measure of the average absolute difference between the discontinuity angles of polygon segments made with its adjoining segments.
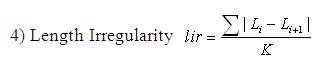
where K = 2P for n > 3 and K = P for n = 3. A normalized measure of the average absolute difference between the length of a polygon segment and that of its preceding segment.
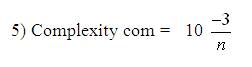
A measure of the number of segments in a boundary group weighted such that, small changes in the number of segments have more effect in low complexity shapes than in high complexity shapes.
6) Right-Angleness, ra=r/n. A measure of the proportion discontinuity angles which are approximately rightangled.
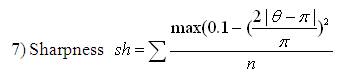 A measure of the pro-
portion of sharp discontinuities (over
90◦).
A measure of the pro-
portion of sharp discontinuities (over
90◦).
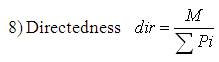
A measure of the proportion of straight-line segments parallel to the mode segment direction.
where, n - number of sides of polygon enclosed by segment boundary, A - area of polygon enclosed by segment boundary, P - perimeter of polygon enclosed by segment boundary, C - length of longest boundary chord, p1, p2 - greatest perpendicular distances from longest chord to boundary, in each half-space either side of line through longest chord, θi-discontinuity angle between (i−1)-th and i-th boundary segment, r – number of discontinuity angles equal to a right-angle within a specified tolerance, and M - total length of straight-line segments parallel to mode direction of straight-line segments within a specified tolerance.
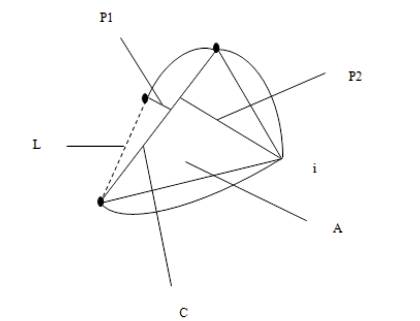
Figure 3. Shape and Measures used to Compute Features
Feature selection (also known as subset selection) is a process commonly used in machine learning, wherein a subset of the features available from the data are selected for application of a learning algorithm. The best subset contains the least number of dimensions that most contribute to accuracy. Feature selection is applied to reduce the number of features in many applications where data has hundreds or thousands of features. The existing feature selection methods mainly focus on finding relevant features. The main objective of feature selection is to choose a subset of input variables by eliminating features, which are irrelevant or of no predictive information. Feature selection has proven in both theory and practice to be effective in enhancing learning efficiency, increasing predictive accuracy and reducing complexity of learning results [21].
Mutual Information (MI) is a measure of the general interdependence between random variables [22].
Specifically, given two random variables (r.v.) X and Y, the mutual information I(X; Y) is defined as follows,
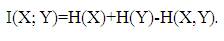
H( ) is the entropy of a random variable and measures the uncertainty associated with it. For a continuous random variable X, H(X) is defined as,
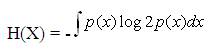
If X is a discrete r. v., H(X) is defined as follows:
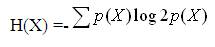
In both cases, p(X) represents the marginal probability distribution of r. v. X. Based on the above formulas, it is apparent why the entropy is often considered a measure of uncertainty. As an example, let the r. v. X represent the presence of disease D.
The MI between two random variables X and Y m~i.e., a texture feature and the PE diagnosis, respectively was estimated using the histogram approach. According to this method, the probability density function of each variable is approximated using a histogram. Then, the MI can be calculated according to the following equation,
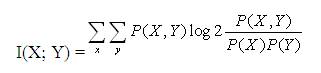
where the summations are calculated over the appropriately discretized values of the random variables X and Y. For each histogram bin, the joint probability distribution P(X,Y) is estimated by counting the number of cases that fall into a particular bin and dividing that number with the total number of cases. The same technique is applied for the histogram approximation of the marginal distributions P(X) and P(Y).
Another popular feature selection technique is the Information gain. IG is frequently employed as a term goodness criterion in the field of machine learning. It measures the number of bits of information obtained for category prediction by knowing the presence or absence of a term in a document. Let {ci}im =1 denote the set of categories in the target space. The information gain of term t is defined to be:
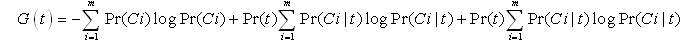
This definition is more general than the one employed in binary classification models.
In this work, gain ratio is used which is a modification of the information gain that solves the issue of bias towards features with a larger set of values, exhibited by information gain. Gain ratio should be large when data is evenly spread and small when all data belong to one branch attribute. Once features are selected by gain ratio, Cuckoo Search is initiated to obtain the best features.
When choosing an attribute, Gain ratio takes the number and size of the branches into account, as it corrects the information gain by considering intrinsic information of a split (how much information is needed to know which branch an instance belongs to) where Intrinsic information is the entropy of the instances distribution into branches.
For a given feature x and a feature value of y, the calculation is as follows:
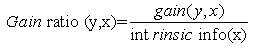
where,
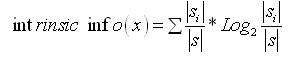
|s| is the number of possible values a feature x can take, and |si| is the number of actual values of feature x.Application of gain ratio to every dataset feature provides an estimate of a feature's importance with all features being ranked from the most influential to the least through the sorting of gain ratios. The top k features, then construct a simple classifier.
Feature selection is used to select the optimal d feature out of total features t. The extracted features can be reduced by FS to remove redundancy and irrelevant features. Wrapper based approach uses induction algorithm as a black box for the feature subset selection. The feature subset selection algorithm searches for a good subset with the induction algorithm itself as part of evaluation function. The accuracy of induced classifiers is estimated using accuracy estimation techniques. A search is done in the space of possible parameters by wrapper based approach where the search requires a state space, an initial state, a termination condition, and a search engine.
In this work, a wrapper based FS with Cuckoo Search (CS) optimization algorithm [23] has been proposed. Generally, cuckoo birds attract attention of many scientists around the world because of their unique behavior. They have a main characteristics which differentiate from others is the aggressive reproductive strategy. For example, some species like Ani and Guira cuckoos lay their eggs in communal nests, even though they may remove others' eggs in order to increase the hatching probability of their own eggs [24]. Cuckoos engage brood parasitism. The brood parasitism is that of a bird (brood parasite) that lays and abandons its eggs in the nest of another species. There are three basic types of brood parasitism such as intraspecific brood parasitism, cooperative breeding, and nest takeover [25]. In that, some host birds do not behave friendly against intruders and engage in direct conflict with them. So the host bird will throw those alien eggs away in that situation. To simplify the description of the novel Cuckoo Search algorithm, three idealized rules are used [26]:
Each egg in a nest is a solution, and a cuckoo’s egg means a new solution. The objective of CS is to use the new and potentially better solutions (cuckoos) to replace a not-so-good solution in the nests. Pseudocode for cuckoo algorithm based feature selection:
Assigning the parameters,
Generation step: t
while (t < G)
for (I = 0, I < C, I++)
{
Move cuckoo to the new nest with step size S,
Calculate fitness given by function Fi
if (Fi > Fj )
{
Fj = Fi ;
}
End for
End while.
The generation of new solutions, x (t+1) is done by using a Lévy flight (equation1). Lévy flights essentially provide a random walk while their random steps are drawn from a Lévy distribution for large steps which has an infinite variance with an infinite mean (equation 2). Here the consecutive jumps/steps of a cuckoo essentially form a random walk process which obeys a power-law steplength distribution with a heavy tail [27].
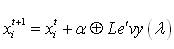
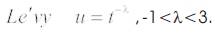
where α > 0 is the step size which should be related to the scales of the problem of interest. Generally, we take α = O(1). The product ⊕ means entry-wise multiplications. This entry-wise product is similar to those used in PSO, but here the random walk via Lévy flight is more efficient in exploring the search space as its step length is much longer in the long run.
The main characteristics of CS algorithm is its simplicity. In fact, comparing with other population or agent-based metaheuristic algorithms such as particle swarm optimization and harmony search, there are few parameters to set.
Pick up the solution (nest) with the maximum egg i.e. maximum fitness. This solution is the output of the feature selection procedure [28]. In this work, the objective is to minimize the error during classification. The fitness function is as follows:
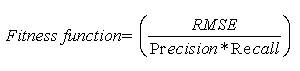
The extracted features are classified using Recurrent Neural Network (RNN). RNN are designed to learn sequential or time varying patterns. A recurrent net is a neural network with feedback (closed loop) connections [29,30]. Examples include Elman, BAM, Hopfield, Boltzmann machine, and recurrent back propagation nets [31]. Recurrent neural network techniques have been applied to a wide variety of problems related to classification, language processing, trajectory problems, and robotic behavior, optimization, filtering and so on.
Recurrent neural network architectures can be in many forms with two common features:
1. Incorporating some form of MultiLayer Perception as a sub-system.
2. Exploiting MultiLayer Perception's powerful non-linear mapping capabilities, plus some form of memory.
Learning is through gradient descent procedures similar to those which derive back-propagation algorithm for feed-forward networks.
RNN architectures include multilayer feed forward networks with specific input and output layers. Networks totally connected do not have specific input node layers. Each node has input from other nodes. Feedback to the node is possible. In simple RNNs (Figure 4) some nodes form part of a feed forward structure, others provide sequential context and receive feedback from other nodes. Context unit (C1 and C2) weights are processed similar to those for input units, for example using back propagation. Context units receive time-delayed feedback from second layer units in Figure 4. Training data include inputs and desired successor outputs.
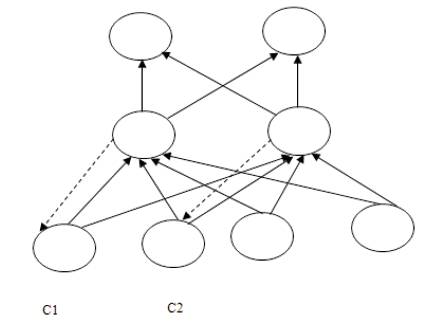
Figure 4. An Example of a Simple Recurrent Network
Elman [32] introduced feedback from hidden layer to the input layers context portion. This method emphasizes input values sequence. Jordan recurrent neural networks [33] use output layer feedback to input layer context nodes emphasizing output values sequences.
As RNN operates in time, at each time step, it accepts an input vector, updates its hidden state via nonlinear activation functions, and uses it to make a prediction of its output. A learning algorithm, Error Back-Propagation Through Time (BPTT) is used for RNN and derived from classic BP to be used on FFNN [34, 35]. Compared to the other learning algorithms, implementing BPTT is relatively easy. The basic of the BPTT algorithm is transformation of RNN “unfolded” to the FFNN comprising more layers, which can be applied to classic BP with minor changes. By the unfolding of RNN, every newly produced layer of FFNN signifies one recursion in time of RNN considered by T - depth of unfolding of RNN.
Updation of the activation state of all the units occurs in prompt moments of time. The initial step comprises the unfolding process of the network that consists in replicating times (folds) the RNN obtaining an equivalent FFNN. In this procedure, at all times, each replicated connection shares its value [36]. The resultant FFNN can be trained now, using the Back propagation algorithm. Actually, this is the chief idea of the BPTT algorithm. The calculation of output time of each neuron, in the forward process of Back propagation, is defined as,
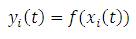
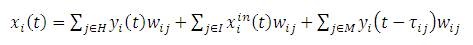
where f refers to the neuron activation function, denotes hidden layers indexes, I and H represents input and hidden neuron indexes respectively, M is the index of neurons which contains information about the previous stages and τij is an integer representing displacement in recurrent connections through time [37].
Since the top 50 features obtained from gain ratio and the proposed Cuckoo Search are used for classification, the size of the input layer was fixed at 50 with one hidden layer consisting of 20% of the neurons used in the input layer.
Selecting the optimal topology of neural network for a particular application is a difficult task. In case of RNN, most methods only introduce topologies in which their neurons are fully connected. However, recurrent neural network training algorithm has some drawbacks such as, getting stuck in local minima, slow speed of convergence and network stagnancy. This paper proposes an improved recurrent neural network trained with a Cuckoo Search algorithm to achieve fast convergence and high accuracy.
In the proposed CSRNN algorithm, each best nest represents a possible solution (i.e., the weight space and the corresponding biases for RNN optimization in this paper). The weight optimization problem and the size of a population represent the quality of the solution. In the first epoch, the best weights and biases are initialized with CS and then those weights are passed on to the RNN. The weights in RNN are calculated. The fitness function should reflect the individual's performance in the current problem. We have chosen 1/me as a fitness function, where me is the average error in the training set. In the next cycle, CS will updated the weights with the best possible solution and CS will continue searching the best weights until the last cycle/ epoch of the network is reached or either the MSE is achieved.
The proposed optimized recurrent neural network is evaluated using a data set containing four different classes of image with 150 in each class totalling 600 images. The experiments are run 10 fold cross validation. The Daubechies wavelet and Huffman coding is used for image compression. Gabor filters are used to extract texture features. Feature selection is achieved through IG, MI and the proposed Cuckoo based feature selection method. The top 50 ranked features of MI and IG are utilized for classifying the medical images.
The design parameters of the proposed recurrent neural network are given in Table 1.

Table 1. Parameters used in the Proposed Model
Sample medical images used in the experimental setup are shown in Figure 5.
The misclassification rate is evaluated using RNN and the Proposed CSRNN for Gabor features and Gabor Shape feature are shown in Figures 6 and 7 respectively.
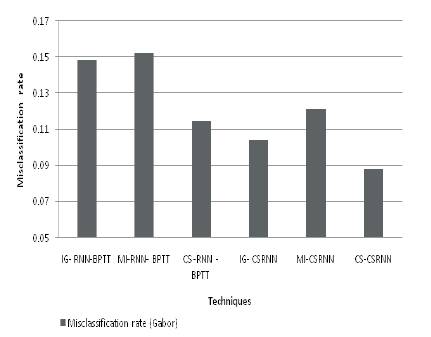
Figure 6. Misclassification Rate for Gabor Features
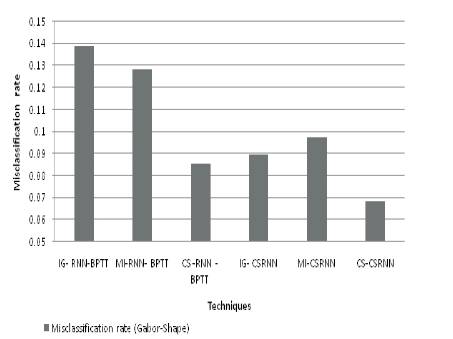
Figure 7. Misclassification Rate for Gabor-Shape Features
It is observed from Figure 6, that the proposed CSRNN with a CS feature selection achieves the least misclassification of 0.088. The feature selection with cuckoo search improves the efficiency of the proposed classifier by reducing the misclassification rate in the range of 16.67% to 53.33%. Precision and Recall for various methods are given in Table 2.
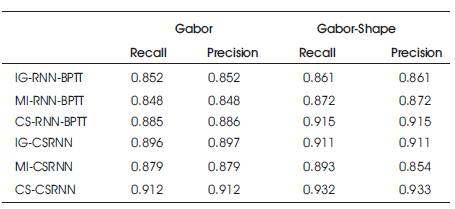
Table 2. Precision and Recall for Various Methods
The proposed method integrates image retrieval to retrieve the diagnostic cases similar to the query medical image and the image compression techniques to minimize the bandwidth utilization. Visually lossless image compression is obtained using the Daubechies wavelet with Huffman coding. Shape and texture features are extracted from the medical compressed medical images using Gabor transforms. 50 top ranked features selected through Gain ratio based on ranking and a Cuckoo based feature selection are used for classification. The classification accuracy of retrieval is evaluated using the proposed partial recurrent neural network. Simulation results achieved are satisfactory.