Modeling of circular data with limited number of available circular models such as, von Mises, Wrapped Cauchy, Cardioid, etc., was done in various domains like Neuro Science, Geography, Archaeology, Remote Sensing, Spatial Analysis, Plant Phenology and Political Science. Dattatreya Rao (2007; 2011a;2011b;2011c; 2013a; 2013b; 2016) and Girija (2010; 2013a; 2013b; 2014a; 2014b), Phani (2012a; 2012b; 2013a; 2013; 2014; 2015a; 2015b; 2015c; 2015d), Radhika (2013a; 2013b; 2014;2015) and Devaraaj (2012; 2014) have introduced several new models and a few new methodologies of constructing the new circular models. These circular models are constructed by applying wrapping method, inverse stereographic projection, offsetting and the rising sun function. It is observed that, the simple projection method is not a much paid attention in constructing circular models. Glancing the literature, semicircular, arc and skewed angular data were observed in the applications and sufficient number of models for such data is not available. Motivated by these points, the authors have introduced semicircular reflected gamma distribution for modelling semicircular data by a simple projection method on reflected gamma distribution. The authors have extend it to the laxial reflected gamma distribution by a simple projection for modeling any arc of arbitrary length, and also the first four trigonometric moments has been derived for the proposed model.
Quite a lot of work was done on circular models defined on the unit circle (Jammalamadaka and Sengupta 2001); (Mardia and Jupp, 2000). In some cases, the directional/angular data do not require full circular models for modeling, this fact is noted in Jones (1968), Guardiola (2004), Byoung and Hyoung, (2008) and Phani et al. (2013a). For example, when sea turtles emerge from the ocean in search of a nesting site on dry land, a random variable having values on a semicircle is well sufficient for modeling such data. Similarly, when an aircraft is lost but its departure and its initial headings are known, a semicircular random variable is sufficient for such angular data. And few more examples of semicircular data are available in Ugai et.al, (1977).
Guardiola (2004) has obtained the semicircular normal distribution by using a simple projection and Byoung and Hyoung, (2008) have developed a family of semicircular Laplace distributions for modeling semicircular data by simple projection. Phani et al. (2013a) constructed some semicircular distributions by applying modified inverse stereographic projection. In this paper, the authors derive the Semicircular Reflected Gamma distribution by projecting Reflected Gamma distribution over a semicircular segment; this distribution generalizes semicircular Laplace distribution (Byoung and Hyoung, 2008). The authors have plot the graphs of the density function for various values of the parameters. Furthermore, the first four trigonometric moments for proposed model are derived and also they extend this model for l-axial Reflected Gamma distribution for modelling any arc of arbitrary length.
Projection is defined by a one-to-one mapping given by,
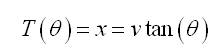
where,
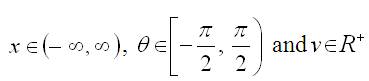
Suppose, x is randomly chosen on the interval (-∞ ,∞ ). Let F(x) and f(x) denote the cumulative distribution and probability density functions of the random variable x respectively. Then,
By Guardiola (2004), equation (2) is a random point on the semicircle. Let, G(θ) and g(θ) denote the cumulative distribution and probability density functions of this random point θ respectively. Then G(θ) and g(θ) can be written in terms of F(x) and f(x) using the following Theorem.
For v > 0,
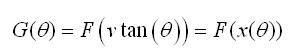
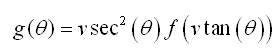
If a linear random variable X has a support on R, then θ has a support on 
and if X has support on R , then θ has a support on 
. These means that, after the projection is applied, we can deal semicircular data if the support of X is on R + and we can handle 4-axial circular data if the support of X is on R+ . Here v is not a parameter; therefore without loss of generality we can assume that v=1.
Here the authors recall the definition of reflected Gamma distribution.
A random variable X on the real line is said to have reflected Gamma distribution with scale parameter λ>0, shape parameter c>0, location parameter α, if the probability density and distribution functions of X are respectively given by,
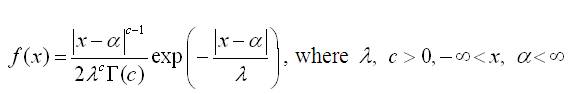
and
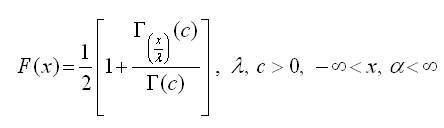
By applying simple projection defined by a one-to-one mapping, x= ν tan(θ), ν >0, which leads to a three parameter symmetric semicircular distribution on unit semicircle.
This distribution is called as Semicircular Reflected Gamma Distribution and it is denoted by SCRG (c,σ,µ).
A random variable XSC on the semicircle is said to have the Semicircular reflected Gamma distribution with shape parameter c, scale parameter σ>0, and location parameter µ, denoted by SCRG ( c,σ,µ), if the probability density and the distribution functions are respectively given by,
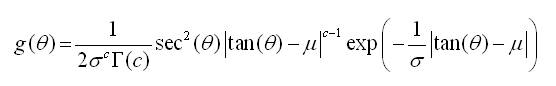
and
where,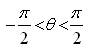
Clearly,
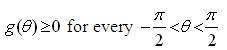
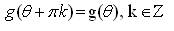
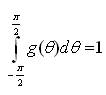
Hence, the proposed new model SCRG (c,σ,µ) is a semicircular model.
When c=1 in (equation 7), we get,
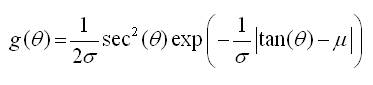
which is semicircular Laplace distribution (Byoung and Hyoung, (2008)).
Figure 1 shows the plots of probability density function of semicircular reflected Gamma distribution for various values of c, σ and µ=0.
Figure 1. Plots of Probability Density Function for values of c, σ and µ=0
It is observed from the plot that the proposed circular distribution is symmetric about µ=0.
The trigonometric moments of the distribution are given by,
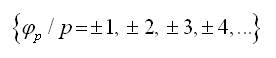
where, φp=αp+iβp, with αp=E(cos pθ) and βp=E(sin pθ) being the pth order cosine and sine moments of the random angle θ, respectively. Since, the Semicircular reflected Gamma distribution is symmetric about µ=0, it follows that the sine moments are zero. Thus φp=αp.
Under the density function of Semicircular reflected Gamma distribution with µ=0, the first four αp=E(cos pθ), p=1,2,3,4 are given as follows:
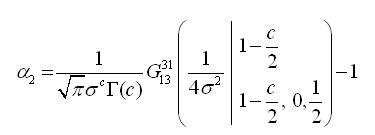
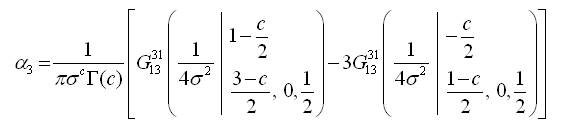
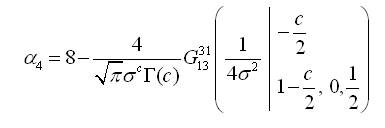
where,
for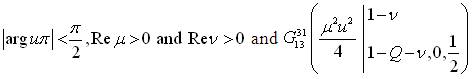 
and is called as Meijer's G-function (Gradshteyn and Ryzhik, 2007, formula no. 3.389.2).
Proof:
The proof is the process of using some transformations. For the first cosine moment, use the transformation 
and then use the property of an even function. So we have the following integral,
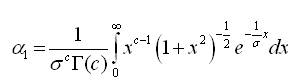
The result α1 follows by the integral formula (Gradshteyn and Ryzhik, 2007).
To obtain second cosine moment α2, we use the transformation 
and the use the property of an even function. So we have the following integral,
The result follows by the same integral formula of α1. To obtain the third cosine moment α3, we use the transformation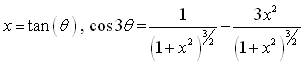 
and the use the property of even function we has the following integral as,
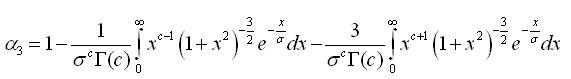
The result follows by the same integral formula of α1.
To obtain the fourth cosine moment α4, we use the transformation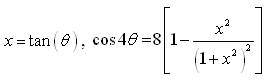 
and the use the property of even function. We have the following integral,
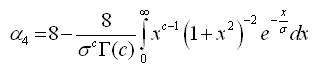
The result follows by the same integral formula of α1.
Higher-order moments can be obtained similarly.
Note that, like any other symmetric circular density, βp=E(sin pθ) are 0 as the density of semicircular reflected Gamma distribution is symmetric about µ=0.
The authors have extend the proposed model to the l-axial distribution, which is applicable to any arc of arbitrary length say 2π/l for l=1,2,... . To construct the l-axial Reflected Gamma distribution, we consider the density function of semicircular reflected Gamma distribution and use the transformation Ψ=2θ/l, l=1,2,.... The probability density function of Ψ is given by,
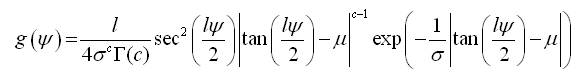
where,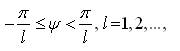
When, l=2, the probability density function (equation 20) is the same as the probability density function of Semicircular reflected Gamma distribution.
When, l=1, the probability density function (equation 20) is
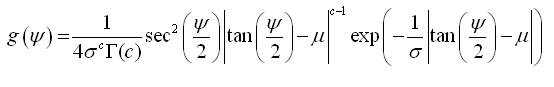
where -π ≤ Ψ < π, which is the probability density function of Stereographic Reflected Gamma Distribution (Phani et al.2012a).
When, l=2 and c=1, the probability density function (equation 20) is
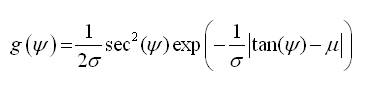
where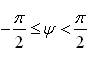 
, which is the probability density function of Semicircular Laplace Distribution (Byoung and Hyoung, 2008).
When, l=1 and c=1, the probability density function (equation 20) is,
where, -π ≤ Ψ < π, which is the probability density function of Stereographic Double Exponential Distribution (Girija et al. 2014b).
For analyzing semicircular data, in various applications like aircraft lost problem, sea turtles emerging from the ocean in search of a nesting site on dry land, etc., the proposed semicircular model is worth trying.
In this paper, the authors have investigated the semicircular distribution which follows by projecting the reflected Gamma distribution onto a semicircular segment. The density and distribution functions of a semicircular reflected Gamma distribution admit explicit forms, as do trigonometric moments. Meijer's G-function played an important role in the derivation of trigonometric moments. Furthermore, the first four trigonometric moments for the proposed model are derived and also the authors have extended this model for l-axial Reflected Gamma distribution for modeling any arc of arbitrary length. As this distribution is symmetric, promising for modeling symmetrical semicircular as well as l-axial data. The Semicircular Reflected Gamma distribution generalizes semicircular Laplace distribution (Byoung and Hyoung, 2008). The authors have plotted the graphs of the density function for various values of the parameters.
The authors thank the referee for their valuable suggestions which have helped in improving the presentation of the paper.
