In this paper, the authors have consider the graph of Mobius function for zero, G(µn(0)). For an integer n≥1, the graph of Mobius function for zero is a graph with vertex set {1, 2, 3, …, n} and an edge, between two vertices a,b if the Mobius function value, µ(ab)=0. The authors have studied the basic results of a graph as the degree of vertex, the adjacency of two vertices and the planarity. First, the authors have calculated the minimum degree and the maximum degree of graph of Mobius function for '0'. The sufficient conditions for two vertices to be adjacent in the graph of Mobius function for '0' based on the divisibility of numbers are discussed and also, proved the necessary and sufficient condition for adjacency of two consecutive vertices in the graph of Mobius function for '0'. At the end, the authors have discussed the planarity of the graph according to the number of vertices of the graph.
The Mobius function in [11, 8] , is a well known function in Number theory and it is defined by µ(1)=1 and if n>1, we write n=p1a1p2a2p3a 3....pkak, then,
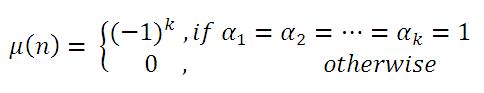
The graph G in [3, 6], is a triple G (V, E, ψ), consisting of a finite set V of elements called vertices with a set E of unordered pair of elements of V called the edges and ψ is the incident relation between vertices and edges. Two vertices u and v are adjacent, if there is an edge e incident with the vertices u and v. The number of edges incident with a vertex u is called the degree of u and it is denoted by d(u). The minimum and maximum degrees of a vertex of a graph are respectively denoted by δ and Δ.
Here we consider the graph, G (V, E) by defining on the powerful arithmetic function called Mobius function. The graph of Mobius function for '0' is denoted by G(µn(0)). Its vertex set is the set of first n natural numbers and the two vertices a, b are adjacent if and only if µ(ab)=0. The Graph theory is closely related to many other branches of Mathematics namely Group theory, Ring theory, Number theory, Topology, etc. In particular, Chalapathi and Madhavi [5] used the symmetry of Group theory in the arithmetic Cayley graph, Anderson and Badawi [1], Eswara Rao and Bharathi [7] [2] worked on the graphs with vertex set as a commutative ring. The use of number theory in the graph theory was first introduced by Nathanson [10]. He used the congruence of two numbers to define the adjacency between two vertices. In 1971, Cadogan [4] used the Mobius function for the calculation of coefficients in the counting series for unlabelled connected graphs. In [12], Vasumathi introduced a new class of graph called Mobius graph. The vertex set of this graph is the first n natural numbers and two vertices of this graph are adjacent if and only if µ(ab)=0. The graphs considered in this paper are all simple graphs.
Vasumathi [12] gives the degree of each vertex of G(µn(0)) as the following lemma.
If u (u ≠ 1) is any vertex in G(µn(0)) then,
and if u=1, then,
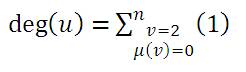
Using the above lemma, the authors discussed the minimum degree and maximum degree of the graph.
Theorem 1:
The minimum degree of the graph,
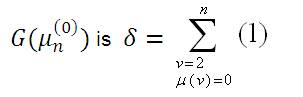
Proof:
Let G(µn(0)) be a graph with n vertices.
From the Lemma 1, the degree of the vertex 1 is given by,
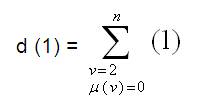
Let u be any vertex of G(µn(0)) such that µ(u)=1, u≠1
Then the vertex u is adjacent to every vertex x such that µ(x) =0, since µ(u.x)=0
Also the vertex u may be adjacent to other vertex y such that µ (y)≠ 0, (u,y)≠1,where y≤n
So, the neighborhood of the vertex u is N(u)= {x/µ(x) =0} U {y/µ(y)≠0, (u,y) ≠ 1}
Thus,
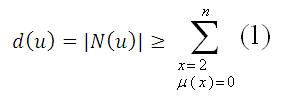
Then, d(u)≥d(1)
Similarly, for any vertex w of G(µn(0)) such that µ(w)=-1
Then the vertex w is adjacent to every vertex x such that µ(x)=0, since µ(w.x)=0
Also the vertex w may be adjacent to other vertex y such that µ (y)≠0, (w,y)≠1, where, y≤n
So, the neighborhood of the vertex w is N(w)= {x/µ(x)=0} U {y/µ(y)≠ 0, (w,y)≠1}
Thus,
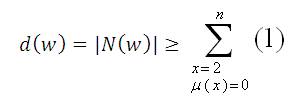
Implies that d(w) ≥ d(1)
Now it is clear that, the degree of the vertex z is d(z) = n-1 such that µ(z) = 0
Thus the degree of the vertex 1 is the minimum degree of the graph G (µn(0))
Hence the minimum degree of the graph,
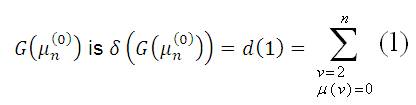
Theorem 2:
The maximum degree of the graph G(µn(0)) is Δ=n-1
Proof:
Let G(µn(0)) be a graph with n vertices
Let u be any vertex such that µ(u)=0
Also let v be any another vertex.
Now, µ(uv)=0
Therefore, u,v are adjacent vertices.
Since, v is an arbitrary vertex, then, u is adjacent to all the remaining vertices.
Since the graph has n vertices and it is a simple graph.
Then, u is adjacent to n-1 vertices.
i.e., d(u) = n-1
Let w be a vertex such that µ(w)≠0
then we have µ(w)=1 or µ(w)=-1
Implies,µ(1,w)=µ(w)=1 or -1≠0
Therefore, w is not adjacent to the vertex 1
And w is adjacent to not more than n-2 vertices.
i.e., d(w)≤n-1
Therefore, the vertex u such that µ(u)=0 has the degree n-1, which is the maximum of the degrees of all the vertices.
Therefore, the maximum degree of the graph, G (µn(0)) is Δ=n-1.
The graph G(µ4(0)) has the minimum degree,δ=1, which is the degree of the vertex 1 and the maximum degree, Δ=4-1=3, which is the degree of the vertex 4 shown in the Figure 1.
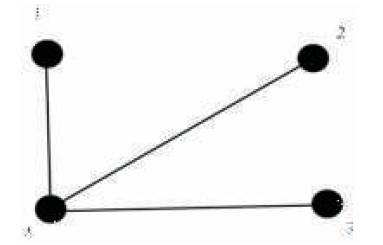
Figure 1. The Graph of Mobius Function for '0' with 4 Vertices, G(µ4(0))
Now, the following theorems describe the adjacency of two vertices based on the divisibility of two vertices.
In the graph G(µn(0)), every pair of distinct prime vertices are not adjacent.
Let G(µn(0)) be a graph
Let p, q be prime vertices in the set of vertices of G (µn(0)) and 1≤ p, q ≤ n, p≠ q
Since p=p1 and q=q1
Let k=pq
Implies, k=p1q1 and p≠q
Implies, µ(k)= (-1)2 = 1
Therefore,µ(pq)=1≠0
Therefore, the vertices p,q in G(µn(0))are not adjacent.
Hence, every pair of distinct prime vertices are not adjacent in G (µn(0))
The graph G(µ13(0)) has the vertices 7, 11, 13 which are distinct primes and there are no edges between them, so that they are not adjacent to each other. It is shown in Figure 2.
If gcd(k,l)≠1 for 1≤ k,l≤n, then k,l are adjacent in G (µn(0)). But, the converse need not be true.
Let k,l are two vertices in the graph G(µn(0) ), 1≤k, 1≤n
If gcd(k,l)≠1
Then, gcd(k,l)>1
We have, k = p1α1 p2α2 ....p3α3 , pi's are primes
l = q1β1 q2β2 ....q3β3 , qj's are primes.
Since, gcd (k,l)≠ 1,
Implies, pi = qj for some i,j
Now,
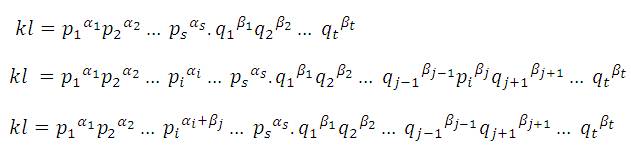
Clearly, αi + βj > 1 and pi’s, qj’s are all primes.
Implies, µ(kl)=0
Therefore, k,l are adjacent in G(µn(0))
The converse need not be true.
Because, in the graph G(µn(0)), n≥5,
The vertices 4 and 5 are adjacent but gcd (4, 5) =1
Hence, if gcd (k,l)≠ 1, then k,l are adjacent in G (µn(0)) but not the converse.
For 1 < k,l ≤ n, if k/l or l/k, then k,l are adjacent in G (µn(0))
Let G(µn(0)) be a graph of Mobius function for 0.
For 1 < k, l ≤ n,
Let k/l or l/k.
If k/l, then gcd(k,l) = k > 1.
Implies, gcd(k,l) ≠ 1 and from Theorem 4,k,l are adjacent in G (µn(0))
If l/k, then gcd(k,l) = l > 1
Implies, gcd(k,l)≠ 1 and from Theorem 4,k,l are adjacent in G (µn(0))
The graph G(µ20(0)) has the vertices 6 and 10 such that gcd (6,10) = 2 ≠ 1 and these vertices 6, 10 are adjacent. Also, 5 and 15 are vertices such that 5/15 and these vertices 5, 15 are adjacent. It is shown in Figure 3.
In a graph G(µn(0)), for 1≤ k < k + 1 ≤ n, k, k + 1 are adjacent vertices if and only if either µ (k) =0 or µ (k+1) = 0.
Let us consider the graph G(µn(0)) with n vertices.
Let us suppose k, k + 1 are adjacent vertices, where, 1≤ k < k + 1≤ n.
Then we have,
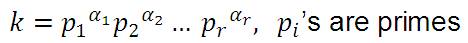
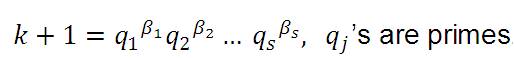
Also, 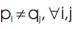
Implies, k.k + 1 = p1α1 p2α2 ....prαr .q1β1 q2β2 ....q3β3
Since, k, k+1 are adjacent vertices in G(µn(0) ) then µ(k.k+1)=0
Then k.k + 1 = p1α1 p2α2 ....prαr .q1β1 q2β2 ....q3β3 has at least one αi or βj is greater than 1.
Then there exists αx or βy such that, αx > 1 and βy > 1, where 1≤ x ≤ r, 1 ≤ y ≤ s.
If αx > 1, then µ(k) = 0, where 1 ≤ x ≤ r.
If βy > 1, then µ(k+1) = 0, where 1 ≤ y ≤ s.
That is if µ (k.k+1) = 0, then µ(k) = 0 or µ (k+1) =0
Thus, if k,k+1 are adjacent in G(µn(0)), then either µ(k) = 0 or µ (k+1) =0, where 1≤k< k +1 ≤ n
Conversely, let us suppose that either µ(k) =0 or µ (k+ 1) = 0, for 1≤ k < k + 1 ≤ n
If µ(k) = 0, then in equation (1), at least one αi is greater than 1, 1 ≤ i ≤ r
then, k.k + 1 = p1α1 p2α2 ....prαr .q1β1 q2β2 ....q3β3 where at least one αi is greater than 1.
Implies, µ(k.k+1) = 0
Similarly, from equation (2), if µ(k+1) = 0, then µ(k.k +1)=0
That is if either µ(k) = 0 or µ(k+1) = 0, for 1 ≤ k < k + 1 ≤ n, then µ (k.k+1) = 0
So that k, k+1 are adjacent in G(µn(0))
Hence, in a graph G(µn(0)), for 1 ≤ k < k + 1 ≤ n, k, k +1 are adjacent vertices if and only if either µ (k) = 0 or µ (k + 1) = 0.
From Figure 3, we can observe that the vertices k=7, k+1=8 are adjacent in G(µ20(0)) and µ(k+1) = 0. Also, the vertices k=12, k+1=13 such that µ(k) = 0 and k,k+1 are adjacent.
If n ≥ 9, then the graph G(µn(0)) is non-planar.
Consider the graph of Mobius function for '0' with n vertices, G (µn(0))
Let us assume that n≥9.
Then the graph has the vertices 3, 4, 6, 8, 9.
Since,µ(4)=µ(8)=µ(9)=0, then the vertices 4, 8, 9 are adjacent to all other vertices in the graph G (µn(0)),n ≥9.
And since, µ(3.6) = 0, then the vertices 3, 6 are also adjacent to each other.
Thus there forms a complete sub graph with the vertices 3, 4, 6, 8, 9 of the graph G(µn(0)), n ≥ 9 which is shown in Figure 4 and it is the Kuratowski's first graph.
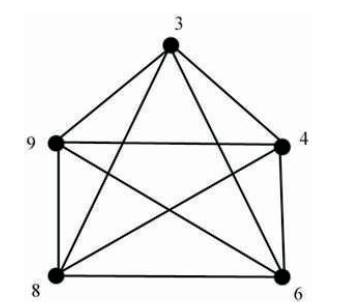
Figure 4. Complete Graph with 5 Vertices, K5
By the Kuratowski theorem in [9],
The graph G(µn(0)), n≥ 9 is a non- planar graph.
By observing the graphs G(µn(0)), n ≤ 8, it is clear that these graphs are planar graphs. For example, Figure 5 shows that the graph G(µ8(0)) is a planar graph.
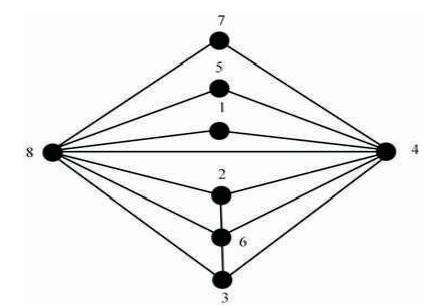
Figure 5. The Graph of Mobius function for '0' with 8 vertices, G(µ8(0))
In this paper, the authors have defined a graph of Mobius function for '0' and have discussed some basic results. This paper is an opening for making another bridge between graph theory and number theory. Here the authors have calculated the minimum degree of this graph by using the value of degree of each vertex and it is found that the degree of the vertex is 1. Next the maximum degree of the vertex is calculated as n-1, where n is the number of vertices of the graph of Mobius function for '0'. Also, proved the sufficient condition for adjacency as, (i) if two vertices are distinct primes then they are not adjacent and (ii) if the greatest common divisor of two vertices is more than 1, then they are adjacent but not the converse. And established the necessary and sufficient condition for two consecutive vertices are adjacent is that, at least one of them has the Mobius function value of '0'. Finally, it is proved that, if the number of vertices are more than 8, then the graph is not a planar graph.