This monograph provides an epistemological rational for the design of an advanced and novel post hoc parametric statistic and meta-analysis metric. “Trichotomous-Cubed Tri- Coordinate Meta-Analysis (“Tri-Cubed Test” also “Tri- Cubed” or “Tri 3”) is an advanced, highly precise research methodology for the accurate in-depth analysis of the existing reported data on a specifically identified criterion. The Tri-Cubed Test integrates and extends the Tri-Squared Test in a Tri- Coordinate [x, y, and z] Tri-Squared Meta-Analysis model and methodology. It is a statistic that involves a variety of robust and rigorous calculations, a precise isometric model, and a series of sequential and detailed computations to provide further insight on the inner workings of the reported statistically significant data. It actively makes use of Tri-Squared Meta- Analysis first presented in the i-managers Journal on Educational Technology and the Tri-Squared Test that was first introduced in the i-managers Journal on Mathematics.
Trichotomous Cubed (or “Tri-Cubed” also “Tri- Cubic” = Tri ) Tri-Coordinate Meta-Analysis is an advanced precision research methodology for the in-depth analysis of existing reported data on an identified criterion beyond (“meta”) existing methods of statistical analysis. The Tri-Cubed Test is a highly advanced type of statistical problem-solving metric similar in some respects to morphological analysis. Tri-Cubic analysis operates in three Cartesian coordinates but in terms of data analysis is grounded in (or “reverts back to”) two Cartesian coordinate data analysis metrics (in particular, the Tri-Squared Test). “Morphological Analysis” or “General Morphological Analysis” is a problem-solving method pioneered and developed by Fritz Zwicky (1967, 1969) for exploring all the possible solutions to a multi-dimensional, non- quantified complex problem (Ritchey, 1998, 2006, 2011, Rothman, Greenland and Lash, 2008, and Rothman, Greenland and Lash, 2012). Traditional Meta-Analysis involves research methods that focus on contrasting and combining results from different studies, in the hope of identifying patterns among study results, sources of disagreement among those results, or other interesting relationships that may come to light in the context of multiple studies (Greenland and O'Rourke, 2008). A dynamic and complex third Trichotomous variable (the Trichotomous Algorithmic Variable or “TAV)” is factored into the data analysis and calculation procedures of the Tri-Squared Test producing the Tri-coordinate nature of the Tri-Cubed Test.
The primary objective of this paper is to introduce a novel statistics procedure into the field of Trichotomous research inquiry. The innovative procedure presented here is referred to as the “Trichotomous-Cubed Tri-Coordinate Meta-Analysis Test” which can be shortened into the “Tri-Cubed Test”. This post hoc statistical measure extends the existing Tri-Squared Test into the realm of Trichotomous mathematical inquiry (generally based upon a researcher designed “Inventive Investigative instrument”). The sole purpose of the Tri-Cubed Test is to analyze existing data using Trichotomous metrics that have additional algorithms that are used to more precisely evaluate the data under investigation. The Tri-Cubed Test procedures are described in detail in the narrative and are followed by an example that illustrates how the procedure is used.
The Tri-Cubed Test data analysis methodology uses the Isometric Cuboid mathematical geometric model from Visualus (Osler, 2010). The Tri-Cubed Meta-Analysis methodology uses a trifold combination of the following:
Tri-Cubed as a Meta-Analysis methodology is constructed around the mathematical Law of Trichotomy which requires an indepth threefold nature to all aspects of data analysis. This infrastructure within Tri-Cubed Meta-Analysis requires the Trichotomous analysis of:
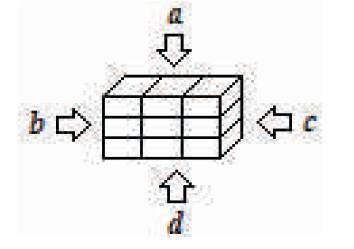
Figure 1. Tri-Cubed Meta-Analysis
The Trichotomous Algorithmic Variable uses a data analysis algorithm that is the basis of the research analysis methodology for the precise examination of the exist data. A Trichotomous Algorithmic Variable is defined by the Tri-Cubed Trichotomous Algorithmic Variable Equation which is a “step by step” procedure for a researcher-defined set of axioms (or a set of mathematical rules for conducting specific calculations). The use of the researcher's Trichotomously defined algorithm (as a detailed method of accurate Trichotomous analysis of existing data) is established at the outset of research. The outcomes of the Trichotomous Algorithmic Variables are reported and then allowed for the use of the Tri-Squared Test within the Tri- Cubed Isometric Cuboid to determine the statistical significance of the Trichotomously Cubed Tri-Coordinate Meta-Analysis.
The Trichotomous Triangulation Model or “Tri-Cubed Trine” = 
3 of the Tri-Cubed Test is shown in Figure 2.
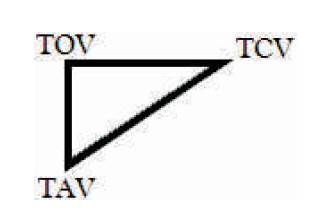
Figure 2. Tr3i Trichotomous Triangulation Model
Here, the Trichotomous Categorical Variable ⇒ (“leads to”) the Trichotomous Outcome Variable ⇒(“leads to”) Trichotomous Algorithmic Variable (“leads back to”) Trichotomous Categorical Variable. Figure 2 illustrates the nature of the relationship between the three Trichotomous variables of the Tri-Cubed Test.
The “Dual Trine” Trichotomous Triangulation model of the Tri-Cubed Test creates the inverted duality of the Trichotomous Triangulation model thereby creating the thirty cells (in row, column, and section format) of the Isometric Cuboid. An example of the dual Trine follows (which creates the “Tri-Cubed Test Trichotomous Algorithmic Indicator” = “
” which in turn become each of the cells in the Tri-Cubed Test Isometric Cuboid) is shown in Figure 3.
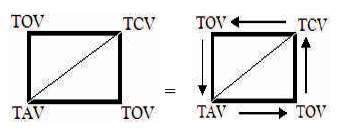
Figure 3. Tri-Cubed Test Trichotomous Algorithmic Indicator
The mathematical hypotheses of the Tri-Cubed Tri-Coordinate Meta- Analysis Test methodology are dual (for the Tri-Cubed Test as a result of the within Tri-Squared hypotheses results) and are described in the next section.
The sequential seven steps that are a part of “Trichotomous Squared Meta-Analysis” consist of a detailed and precise series of sequential operations designed to aid the researcher in conducting in-depth inquiry on existing data. Sample data is used in this example to illustrate exactly how Tri-Squared Meta-Analysis is used. The steps in the data analysis research procedures for the Trichotomous Squared Meta-Analysis conducted in the example study included the following:
The Trichotomous confirmatory data analysis mathematical hypotheses of the Tri-Cubed Test are dual meaning that they involve external (or general hypothesis testing) based upon an internal Tri-Squared Test hypothesis test. Thus the mathematical hypothesis test of the Tri-Cubed Test is written in the following manner:
A Sample of Two-Tailed Tri-Cubed Test Confirmatory Data Analysis Mathematical Hypotheses:
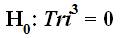
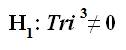
A Sample of corresponding within Tri-Cubed Test Two-Tailed Tri-Squared Confirmatory Data Analysis Mathematical Hypotheses:
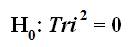
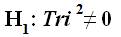
The results of the second set of mathematical hypotheses will directly influence the outcome of the first set of Tri-Cubed Test mathematical hypotheses.
Trichotomous Tri-Coordinate Meta-Analysis (Tri3 ) is composed of the following:
1. TCV=Tri3[TCV] = The Tri-Cubed Test Trichotomous Categorical Variable (represented by the Tri-Coordinate Planar Vector “a” = Cartesian Coordinate “x” = the abscissa);
2. TOV = Tri3[TCV] = The Tri-Cubed Test Trichotomous Outcome Variable (represented by the Tri-Coordinate Planar Vector “b” = Cartesian Coordinate “y” = the ordinate); and
3.TAV= Tri3[TAV] = The Tri-Cubed Test Trichotomous Algorithmic Variable (represented by the Tri-Coordinate Planar Vector “c” = Cartesian Coordinate “z” = the applicate) and is the mathematical data analysis methodology established by the researcher to analyze the reported research defined existing data (thereby allowing the research to be reported in the Tri- Cubed Isometric Cuboid. The TAV is defined by the Tri-Cubed Trichotomous Algorithmic Variable Equation (or the “Tri- Cubed TAV Equation”) which is comprehensively defined in the following manner: Tri-Cubed TAV = Tri3[TAV] = Determination of nTri [the specific number of the reported data outcomes under meta-analysis] for the Trichotomous comparison of either:
Mathematically, in terms of the entire Tri-Cubed Test, this is defined by a holistic TAV equation in the following manner: Tri- Cubed TAV [symbolized by the Tri-Cubed Test Trichotomous Algorithmic Indicator = “ ”] which is = Tri3[TAV] = (nTri = [a pre- determined positive real number which is an absolute value integer]) “ ∀” [meaning “for all”] Tri[ < vs. > or = vs. ≠] [which is the “Trichotomous Mathematical Comparison” = Tri[ < v > v = v ≠] “⇒” [meaning “for either”] Results “∨” [which is the mathematical set theory symbol for “or”] Reports. The mathematical parsimonious form of the equation is written thusly, =[nTri=|R|]∀Tri[ < v > v = v ≠] ⇒ Results ∨ Reports.
In terms of the Tri-Cubed Test Trichotomous Algorithmic Variables, the equation has the following form (without the Trichotomous algorithmic indicator):
The Tri-Cubed Test Trichotomous Triangulation of data is an advanced form of Meta-Analysis that systematically and sequentially analyzes Trichotomous Categorical Variables = Tri3[TCV] , Trichotomous Outcome Variables = Tri3[TOV , and Trichotomous Algorithmic Variables Tri3[TAV] = [ ]. In addition, one cell of the 18 Tri-Cubed Test qualitative results (9ab) and quantitative outcomes (also 9ab) is equal to Tri3[TAV] represented holistically as [ ]. As a mathematical model, the Tri-Cubed Test uses the Visualus Isometric Cuboid Surface area equation [2(9ab + 3bc + 3ac)] which formulates the “Trichotomous- Cubed Tri-Coordinate Test Meta-Analysis Reporting Structure” as follows:
The Surface Area of the Visualus Isometric Cuboid = [2(9ab + 3bc + 3ac)] = [18ab + 6bc + 6ac)] = [
(with a Volume = [v = 9abc] = the Cartesian Tri-Coordinates 9xyz) (Osler, 2010).
Thus, Figure 4 applies to the Tri-Cubed Test.
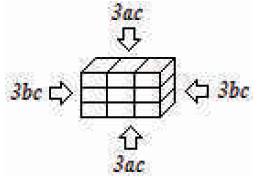
Figure 4. Tri-Cubed Test with Isometric Cuboid
From Figure 4, the Front and Back of the Isometric Cuboid are 9ab respectively.
The Six Isometric Cuboid definitions and order of operations are as follows:
Thus, the complete “Trichotomous-Cubed Test Equation” (that contains the internal Tri-Squared Test Calculation) in definitive mathematical model form can be written in the following format:
Tri3 = [ 
3]x[y][z] •3 = 9xyz = 9abc (where “abc” are “Tri-Coordinate Planar Vectors” of the Isometric Cuboid Cartesian Coordinates “xyz”), contained within the Tri3 Test Equation is the computation of Tri2 = [ 2]x [y] • 3 = 9xy = 
.
In order to acquire the data for the Tri-Cubed Test internal Isometric Cuboid Tri-Squared Test, a researcher-designed Inventive Investigative Instrument must be constructed to “observationally meta-analyze” the existing data that is under rigorous investigation. The process used to construct the Tri-Cubed Test Tri- Coordinate Meta-Analysis Inventive Investigative Instrument is illustrated in Figure 5.
Figure 5. The Tri-Cubed Test Tri-Coordinate Meta- Analysis Inventive Investigative Instrument Metric that is Trichotomously Invariant (or “Trichotmously Unchanging”) used to Create Instrumentation for the Researcher's Observational Analysis of Existing Data
Tri-Square or Tri-Squared comprehensively stands for “The Total Transformative Trichotomous-Squared Test” (or “Trichotomy-Squared”) it provides a methodology for the transformation of the outcomes from qualitative research into measurable quantitative values that are used to test the validity of hypotheses. It is based on the mathematical “Law of Trichotomy”. In terms of mathematics, Apostol in his book on calculus defined “the Law of Trichotomy” as: Every real number is negative, 0, or positive. The law is sometimes stated as “For arbitrary real numbers a and b, exactly one of the relations a < b, a = b and a > b holds” (Apostol, 1967). It is important to note that in mathematics, the law (or axiom) of trichotomy is most commonly the statement that for any (real) numbers x and y, exactly one of the following relations holds. Until, the end of the 19th century, the law of trichotomy was tacitly assumed true without having been thoroughly examined (Singh, 1997). A proof was sought by Logicians and the law was indeed proved to be true. If applied to cardinal numbers, the law of trichotomy is equivalent to the axiom of choice. More generally, a binary relation R on X is trichotomous if for all x and y in X exactly one of xRy, yRx or x = y holds. If such a relation is also transitive, it is a strict total order; this is a special case of a strict weak order. For example, in the case of three elements, the relation R given by aRb, aRc, bRc is a strict total order, while the relation R is given by the cyclic aRb, bRc, cRa is a non-transitive trichotomous relation. In the definition of an ordered integral domain or ordered field, the law of trichotomy is usually taken as more foundational than the law of total order, with y = 0, where 0 is the zero of the integral domain or field. In set theory, trichotomy is most commonly defined as a property that a binary relation < has when all its members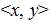 
satisfy exactly one of the relations listed above. Strict inequality is an example of a trichotomous relation in this sense. Trichotomous relations in this sense are irreflexive and anti-symmetric (Sensagent, 2012) .
The foundational idea of a “Trichotomy” has a detailed long history that is based in discussions surrounding higher cognition, general thought, and descriptions of intellect. Philosopher Immanuel Kant adapted the Thomistic acts of intellect in his trichotomy of higher cognition — (a) understanding, (b) judgment, (c) reason — which he correlated with his adaptation in the soul's capacities — (a) cognitive faculties, (b) feeling of pleasure or displeasure, and (c) faculty of desire (Kant, 2007). The Total Transformative Trichotomous-Squared Test provides a methodology for the transformation of the outcomes from qualitative research into measurable quantitative values that are used to test the validity of hypotheses. The advantage of this research procedure is that, it is a comprehensive holistic testing methodology that is designed to be a static way of holistically measuring categorical variables directly applicable to educational and social behavioral environments, where the established methods of pure experimental designs are easily violated. The unchanging base of the Tri-Squared Test is the 3 × 3 Table based on the Trichotomous Categorical Variables and the Trichotomous Outcome Variables. The emphasis the three distinctive variables provide a thorough rigorous robustness to the test that yields enough outcomes to determine if differences truly exist in the environment in which the research takes place (Osler, 2013).
Tri-Squared is grounded in the combination of the application of the research of two mathematical pioneers and the author's research in the basic two dimensional foundational approaches that ground further explorations into a three dimensional Instructional Design (Osler, 2012). The aforementioned research includes the original dissertation of optical pioneer Ernst Abbe, who derived the distribution that would later become known as the chi square distribution and the original research of mathematician Auguste Bravais who pioneered the initial mathematical formula for correlation in his research on observational errors. The Tri-Squared research procedure uses an innovative series of mathematical formulae that do the following as a comprehensive whole:
(1) Convert qualitative data into quantitative data;
(2) Analyze inputted trichotomous qualitative outcomes;
(3) Transform inputted trichotomous qualitative outcomes into outputted quantitative outcomes;
(4) Create a standalone distribution for the analysis possible outcomes and to establish an effective-research effect size and sample size with an associated alpha level to test the validity of an established research hypothesis (Osler, 2012).
The process of designing instruments for the purposes of assessment and evaluation is called “Psychometrics”. Psychometrics is broadly defined as the science of psychological assessment (Rust & Golombok, 1989). The Tri- Squared Test pioneered by the author, factors into the research design a unique event-based “Inventive Investigative Instrument” (Osler, 2013). This is the core of the Trichotomous-Squared Test. The entire procedure is grounded in the qualitative outcomes that are inputted as Trichotomous Categorical Variables based on the Inventive Investigative Instrument (Osler, 2013). Osler (2012) initially defined the Tri-Squared mathematical formula in the i-manager's Journal on Mathematics article entitled, “Trichotomy-Squared - A novel mixed methods test and research procedure designed to analyze, transform, and compare qualitative and quantitative data for education scientists who are administrators, practitioners, teachers, and technologists” as follows:
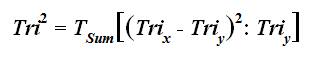
Figure 6 and 7 follow and illustrate the Tri-Cubed Test research reporting procedure in a tabular format.
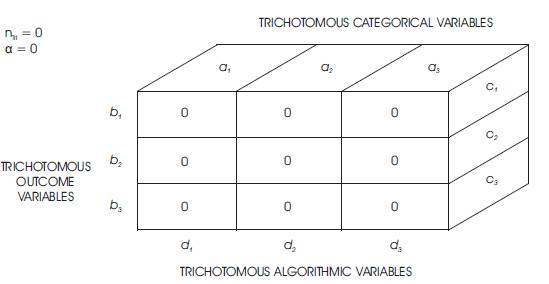
Figure 6. An Orthogonal Table Reporting the Qualitative Results of the Tri-Cubed Tri-Coordinate Meta-Analysis Test as the within Front Planar Vector of the Isometric Cuboid Tri-Squared Test based upon Trichotomous Categorical, Outcome, and Algorithmic Variables
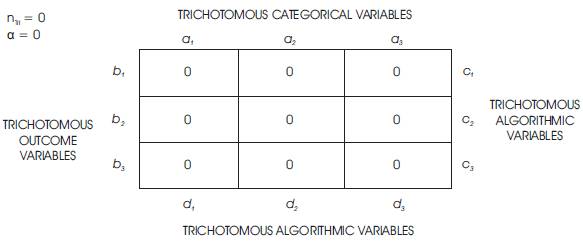
Figure 7. The Final Tri-Cubed Tri-Coordinate Meta- Analysis Test Quantitative Results as the Back Planar Vector of the Isometric Cuboid
List of Tri-Cubed Test Trichotomous Categorical Variables:
a1 = The first Trichotomous Categorical Variable is defined as…;
a2 = The second Trichotomous Categorical Variable is defined as…; and
a3 = The third Trichotomous Categorical Variable is defined as…
List of Tri-Cubed Test Trichotomous Outcome Variables:
b1 = The first Trichotomous Outcome Variable is defined as…;
b2 = The second Trichotomous Outcome Variable is defined as…; and
b3 = The third Trichotomous Outcome Variable is defined as…
List of Tri-Cubed Test Trichotomous Algorithmic Variables:
c1 = The first Trichotomous Algorithmic Variable is defined as…;
c2 = The second Trichotomous Algorithmic Variable is defined as…; and
c3 = The third Trichotomous Algorithmic Variable is defined as…
List of Tri-Cubed Test Trichotomous Algorithmic Variable Outcomes:
d1 = The results of the first Trichotomous Algorithmic Variable…;
d2 = The results of the second Trichotomous Algorithmic Variable…; and
d3 = The results of the third and final Trichotomous Algorithmic Variable…
Figure 7 follows and displays the final Tri-Cubed Test Tri-Coordinate Meta-Analysis quantitative results as the back planar vector of the Isometric Cuboid.
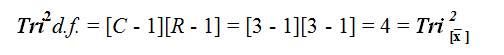
Once the Tri-Cubed Meta-Analysis data has been placed into the front planar vector of the Isometric Cuboid, a traditional Tri2 Test can be calculated. The Tri2 Test total calculations according to table cell, rows, and columns (according to TAV sections) are then computed. The results are reported and transformed into a quantitative data using the Tri2 Test calculation and are illustrated in a tabular format on the final back nine cell Isometric Cuboid planar vector (thereby completing the Tri- Cubed Tri-Coordinate Meta-Analysis reporting structure).
The final hypothesis testing results of the Tri-Cubed Tri-Coordinate Meta-Analysis Test are calculated by obtaining the Tri- Squared Test Critical Value using the Tri-Squared mathematical formula:
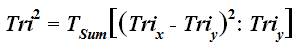
By testing it, against the Tri-Squared Critical Value at the initially specified sample size and alpha level.
A Sample Tri-Cubed Meta-Analysis by using Existing Data is shown in Figure 8.
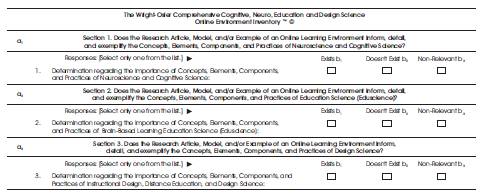
Figure 8. The Sample Research Analytic: A Condensed Interdependent and Independent Inventive Investigative Instrument Designed to Determine the Outcomes of an In-Depth Tri-Squared Meta- Analysis [Under the Standard Conventions of a Tri-Squared Inventive Investigative Instrument] (Osler & Wright, 2015)
Figure 9 is a sample Trichotomy-Squared Test illustrating the standard 3 × 3 Tri-Squared Formula and qualitative table of outcomes reporting results using the standard Tri-Squared 3 × 3 Format. Sample data analyzed using the Trichotomous TSquare Three by Three Table was designed to analyze the research questions from an Inventive Investigative Instrument with the following Trichotomous Categorical Variables (Figure 9):
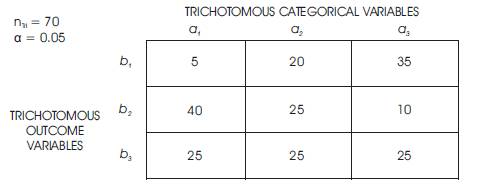
Figure 9. Cognitive Science and Neuroscience in Distance Education Tri-Squared Test Research Analysis
a1 = Importance of Concepts, Elements, Components, and Practices of Neuroscience and Cognitive Science;
a2 = Importance of Concepts, Elements, Components, and Practices of Brain-Based Learning and Education Science (Eduscience); and
a3 = Importance of Concepts, Elements, Components, and Practices of Instructional Design, Distance Education, and Design Science.
The 3 × 3 Table has the following Trichotomous Outcome Variables:
b1 = Exists;
b2 = Doesn't Exist; and
b3 = Non-Relevant.
The Inputted Qualitative Outcomes are reported in equations (7) and (8).
The Tri-Square Test Formula (equation 7) for the Transformation of Trichotomous Qualitative Outcomes into Trichotomous Quantitative Outcomes to determine the Validity of the Research Hypothesis as given in equation (8).
Tri2 Critical Value Table = 9.488 (with d.f. = 4 at α = 0.05). For d.f. = 4, the Critical Value for p > 0.05 is 9.488 (Osler & Wright, 2015).
Qualitative Results of the Tri-Cubed Tri-Coordinate Meta-Analysis Test as within the Front Planar Vector of the Isometric Cuboid Tri-Squared Test based upon Trichotomous Categorical, Outcome, and Algorithmic Variables is given in Figure 10.
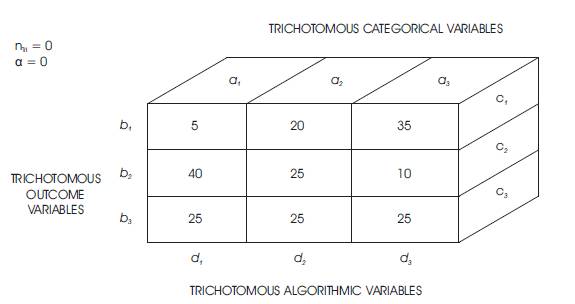
Figure 10. An Orthogonal Table Reporting the Qualitative Results of the Tri-Cubed Tri-Coordinate Meta-Analysis Test as the within Front Planar Vector of the Isometric Cuboid Tri-Squared Test based upon Trichotomous Categorical, Outcome, and Algorithmic Variables
List of Tri-Cubed Test Trichotomous Categorical Variables:
a1 = The first Trichotomous Categorical Variable is defined as “Importance of Concepts, Elements, Components, and Practices of Neuroscience and Cognitive Science”;
a2 = The second Trichotomous Categorical Variable is defined as “Importance of Concepts, Elements, Components, and Practices of Brain-Based Learning and Education Science (Eduscience) ”; and
a3 = The third Trichotomous Categorical Variable is defined as “Importance of Concepts, Elements, Components, and Practices of Instructional Design, Distance Education, and Design Science”.
List of Tri-Cubed Test Trichotomous Outcome Variables:
b1 = The first Trichotomous Outcome Variable is defined as “Exists”;
b2 = The second Trichotomous Outcome Variable is defined as “Doesn't Exist”; and
b3 = The second Trichotomous Outcome Variable is defined as “Doesn't Exist”; and
List of Tri-Cubed Test Trichotomous Algorithmic Variables:
c1 = The first Trichotomous Algorithmic Variable is defined as “Tri-Squared Mean Cross Comparative Analysis Within Column a1 Mean Comparisons (Osler, 2013) ”;
c2 = The second Trichotomous Algorithmic Variable is defined as “Tri-Squared Mean Cross Comparative Analysis Within Column a2 Mean Comparisons (Osler, 2013) ”; and
c3 = The third Trichotomous Algorithmic Variable is defined as “Tri-Squared Mean Cross Comparative Analysis Within Column a3 Mean Comparisons (Osler, 2013) ”.
List of Tri-Cubed Test Trichotomous Algorithmic Variable Outcomes:
d1 = The results of the first Trichotomous Algorithmic Variable “Using the AMOVA [Accumulated Manifold Validation Analysis] statistic's [Weighted Categorical Mean] =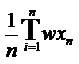 
(Osler, 2015)”;
d2 = The results of the second Trichotomous Algorithmic Variable “Using the AMOVA [Accumulated Manifold Validation Analysis] statistic's [Weighted Group Mean] =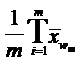 
(Osler, 2015)”; and
d3 = The results of the third and final Trichotomous Algorithmic Variable “Using the AMOVA [Accumulated Manifold Validation Analysis] statistic as the “concentration” on the “Manifold Mathematical Mean” (or the “Concentrated Manifold Arithmetic Average”) = [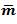
] = mvalue = psy[ri] = [n/m] = [1:m] 
[1:n] (Osler, 2015)”.
The sample data two-tailed Tri-Cubed Test Confirmatory Data Analysis mathematical hypotheses is given in equations (1) and (2).
As such, the Tri-Cubed Test upholds the initial Tri-Squared Meta- Analysis results as follows:Tri2 = Tri3 for Critical Value Table = 9.488 (with degrees of freedom (“d.f.”)= 4 at α = 0.05). Thus, d.f. = 4, the Critical Value for p > 0.05 [at nTri = 70] is 9.488. The Calculated Tri-Cubed Meta-Analysis Value is 40.5 (as Tri2 ≡Tri3 ; by virtue of identical trichotomous meta- analysis procedures based upon the mathematical logical equality of “Tri2 ⇔Tri3 ”), thus, [the null hypothesis (H0 ) is rejected (H0 : Tri3 = 0) by virtue of the Tri-Cubed (and Tri-Squared) hypothesis test which yields the following: Tri-Cubed Test Critical Value of 9.488 < 40.5 the Calculated Tri-Cubed Test Value].
Figures 9 and 10 both illustrate the qualitative transformation into quantitative data as a mathematical application of the Trichotomous-Squared (“Trichotomy-Squared”, “Tri- Squared” or “Tri-Square”) statistical Meta-Analysis procedure on 70 research articles that pertain to current advances in distance education. The final Table shows that the research primarily and overwhelmingly does not include the use of cognitive science, neuroscience, and the science of design to increase the overall effectiveness of distance education courses (a1 b3 , a2 b3 , and a3 b3 all equal to 25) (Osler & Wright, 2015). The mathematical formula for the Tri-Squared Meta-Analysis is reported above further illustrates through direct application the final outcome of the research hypothesis test: the null hypothesis (H0 ) is rejected at p > 0.05 is 9.488 (Osler, 2012). Thus, this illustrates that there is a clear lack of relevant research regarding the use of cognitive science, neuroscience, and the science of design to truly create effective and engaging distance education online courses. The area of focus in which the independent researcher-designed Inventive Investigative Instrument was used was to address the deficits in the application of cognitive science, neuroscience, and the science of design in online learning. As stated in the first Table Research Report, the null hypothesis (H0 ) is rejected by virtue of the Tri-Squared hypothesis test which yields the following: Tri-Cubed Critical Value of 9.488 < 40.5 the Calculated Tri-Cubed Value. Thus the alternative hypothesis is accepted that states: Ha : There will be significant differences in the research literature as it relates to the use of cognitive science, neuroscience, and the science of design to increase the overall effectiveness of distance education course design (Osler & Wright, 2015).
The implications for The Tri-Cubed Test as a post hoc model for conducting in-depth investigative research on existing data is exceptionally positive. By using this research methodology, inquiry can be conducted on existing findings via rigorous exploration of trichotomous research questions and trichotomous mathematical algorithms. This adds a rich value to the field of trichotomous inquiry by allowing researchers to engage additional existing “Triostatistics” (Osler,2014) into their metaanalysis via the Tri-Cubed Test “Trichotomous Algorithm Variable” (TAV) portion of the model. This also makes the Tri-Cube Test the link capable of bridging the research gap that may exist between all of the many other post hoc Triostatistics methodologies. It essentially becomes the “nexus” or meeting point for different post hoc trichotomous statistical methodologies. This greatly aids in unifying advanced trichotomous research. It also aids in making trichotomous-test research, a more approachable field to non-native research investigators who are new (or “newly minted”) to the advanced post hoc trichotomous research. The very nature of the Tri-Cubed Test affords the field of trichotomous research a more practical utility that is highly usable to the greater research community who are interested in discovering the research outcomes on existing data and conducting research on said data in and of itself.
The author recommends the following in regards to future research that will be conducted with the Tri-Cubed Test:
1) That researchers continue to explore research on “Inventive Investigative Instruments” to become familiar with the process of building psychometric research tools native to the Tri-Cubed Test and Tri-Squared Test;
2) That researchers explore research on “Triostatistics” to become familiar with the many post hoc research methodologies that are available for Tri-Cubed Test “Trichotomous Algorithmic Variables”;
3) That researchers explore research on the “Tri-Squared Meta- Analysis” to become familiar with the complete process native to post hoc trichotomous research meta-analysis.
The Tri-Cubed Tri-Coordinate Meta-Analysis Test provides a robust way for analyzing existing data on a variety of topics and with a diversity of subject matter. The post hoc nature of the test and its grounding in a researcher-based rigorous data assessment algorithmic (via the Trichotomous Algorithmic Variable) provides a new level of Tri-Coordinate flexibility to the traditional Tri- Squared Test. This novel approach to statistics lends credibility, feasibility, and reliability to observational analysis procedures. As such, detailed and precise observational analytics can now be designed to explore the in-depth ramifications and implications of historical or existing data. In addition to the aforementioned rationale the Tri-Cubed Test adds to the overall functionality of the Tri-Squared Test, thereby enabling it to be applied to research that has been previously conducted. This greatly increases the applicable uses of Tri-Square by making it highly functional in a variety of statistical settings. This statistical ergonomic multiplicity increases the utility of the test by making it more approachable and highly adaptable. Such usability makes the Tri-Square series of post hoc tests more viable, dynamically engaging, and rigorously empowering for and to all researchers that chose to use it in their investigations. The increased use of measures such as these will open new areas of inquiry in variety of research fields. It will enable researchers to uncover answers that can only be found by conducting inquiry on existing data. The Tri-Cubed Test has the capacity to make existing data and its results more plausible and more approachable to the overall landscape of learning. It does this by encouraging the investigation, inspection, and examination of research outcomes that can be found in the wealth of data and information resources that are in existence and are readily available to be explored.
