---

The word “Veda” has the derivational meaning i.e, the fountain head and illimitable store-house of all knowledge. This derivation, in effect, means, connotes and implies that the Vedas should contain within themselves all the knowledge need by mankind relating to not only to the so-called 'spiritual' matters but also to those usually described as purely 'secular', 'temporal' or “wordy” and also to the means required by humanity as such for the achievement of all round, complete and perfect success in all conceivable directions and that there can be no adjectival or restrictive epithet calculated to limit that knowledge down in any sphere, any direction or any respect whatsoever.

In other words, it connotes and implies that our ancient Indian vedic lore should be all-round, complete and perfect and able to throw the fullest necessary light on all matters which any aspiring seeker after knowledge can possibly seek to be enlightened on.

It is thus in the fitness of things that the Vedas include:

• Ayurveda (anatomy, physiology, hygiene, sanitary science, medical science, etc.) not for the purpose of achieving perfect health and strength in the after-death future but in-order to attain them here and now in our present physical bodies;
• Dhanurveda, (archery and other military sciences) not for fighting with one another after our transportation to heaven but in order to quell and subdue all invaders from abroad and all insurgents from within;
• Gandharva Veda (the science and art of music);
• Sthapatya Veda (engineering, architecture, etc., and all branches of mathematics in general).

 

All these subjects are inherent parts of the Vedas i.e are reckoned as “spiritual studies” and catered there in.

Similar is the case with regard to the Vedangas i.e, (Grammar, astronomy, Lexicography, etc.) which, according to the Indian cultural conceptions, are also inherent parts and subjects of Vedic i.e, Religious study.

Kansara [10] studied “Vedic sources of Vedic Mathematics” in “Indian Journal Sambodhi”, Vol XXIII, 2000.

Dhara Kothari [11] studied about “The power of Vedic Maths” in “The Sunday Observer (India)”, 2-8 July, 2000.

James Glover [13] has published “Everything Vedic in Vedic Maths” in “The Hindu”, Oct 2014.

Jai Sachith Paul [15] has studied “Vedic Mathematics in Microcontrollers” in “Electronics for You” in Feb 2015.

How did Vedic Mathematics Begin?

Vedic Mathematics was not known to the world till it was rediscovered by Swami Bharati Krishna Tirtha (1884-1960), former Jagadguru Sankaracharya [1] of Puri culled a set of 16 Sutras (aphorisms) and 13 Sub - Sutras (corollaries) from the Atharva Veda. He developed methods and techniques for amplifying the principles contained in the aphorisms and their corollaries, and called it Vedic Mathematics. Swami was a great scholar of Sanskrit, Mathematics, History, and Philosophy. His deep study and careful research had deciphered the great mathematical formulas known as sutras. It is considered as the first work towards Vedic mathematics.

According to him, there has been a considerable literature on Mathematics in the Veda-sakhas. Unfortunately, most of it has been lost to humanity as of now. This is evident from the fact that while, by the time of Patanjali, about 25 centuries ago, 1131 Veda - sakhas were known to the Vedic scholars, and now only about ten Veda - sakhas are presently in the knowledge of the Vedic scholars in the country.

In the late 1960s, a copy of his book reached London and from there, Vedic Mathematics was reborn. It was taken up as a new alternative system of Mathematics. British Mathematicians got interested in Vedic Mathematics. Several lectures on Vedic Mathematics were published as a book titled – “Introductory lectures on Vedic Mathematics”. After the visit of Andrew Nicholas to India between 1981 and 1987, interest in Vedic Mathematics started to develop in India (by Swami Sri Bharati Krishna Thirtaji [1]).

It cuts the time and speed up the calculations whereby simplifying the entire process, Vedic Mathematics is getting popular amongst academicians worldwide as a mental system of arithmetic (Atul Gupta in “The Power of Vedic Maths” [6]). Another reason for its adoration is the deepening Mathematics crisis, low global numeracy levels and lack of Mathematics teachers.

Consider this for a moment,

• Currently in the UK, 17 million adults have the mathematics capabilities of an 11 year old or younger. (Source: The Telegraph, UK).
• 9-10 year old and 13-14 year old in the United States continue to lag behind several East Asian and European nations in Mathematics (Source: The New York Times).
• In India in 2012, 46.5% of children in Class V could not solve a two-digit subtraction problem without seeking help (Source: The Pratham Report).
• South Africa ranks second last in the world for education in Mathematics (Source: World Economic Forum).

 

In such a grim scenario in Mathematics, students and teachers too dislike Mathematics. They run away from it and develop a phobia towards the subject. Hence, making Mathematics fun and interesting becomes a challenge. Now this is where Vedic Mathematics steps in through its out of the box methods approach and makes learning Mathematics enjoyable and pleasant for everyone. Vedic Mathematics shorter, quicker and easy to remember with its techniques enable any one to do calculations faster than they would with conventional methods ( Vandana Singhal [5] & James Glover [14]).

It is to find that exceedingly tough mathematical problems which are solved with utmost difficulty and after vast labour involving large number of difficult, tedious and cumbersome steps of working can be easily and readily solved with the help of these ultra-easy Vedic sutras contained in the Parisista of Atharva Veda in a few simple steps and by methods which can be thoroughly described as mere “Mental Arithmetic”.

By Swami Sri Bharati Krishna Thirtaji [1] & Alok Kumar [4] & Kenneth Williams [12] describes the 16 sutras in Vedic mathematics in Table 1.

Some applications of Sutras in day-to-day activities ( James T. Glover [8] & SCERT, New Delhi in “Fundamentals and Applications of Vedic Mathematics [9]) are explained below:

2.1 Ekadhikena Purvena

The Sutra means: “By one more than the previous one”.

Example: Squares of numbers ending in 5:

Now the sutra is relatedto the 'squaring of numbers ending in 5'. Consider the example 25².

Here the number is 25. The square of the number is to be found out. For the number 25, the last digit is 5 and the 'previous' digit is 2. Hence, 'one more than the previous one', that is, 2+1=3. The Sutra, in this context, gives the procedure to multiply the previous digit 2 by one more than itself, that is, by 3.

It becomes the L.H.S (Left Hand Side) of the result, that is, 2 X 3 = 6. The R.H.S (Right Hand Side) of the result is 5² , that is 25. Thus 25² = 2 X 3 / 25 = 625.

In the same way,

35² = 3 X (3+1) /25 = 3 X 4/ 25 = 1225;

65² = 6 X 7 / 25 = 4225;

105² = 10 X 11/25 = 11025;

135² = 13 X 14/25 = 18225;

2.2 Nikhilam Navatascaramam Dasatah

The formula simply means: “all from 9 and the last from 10”.

The formula can be very effectively applied in the multiplication of numbers, which are nearer to the bases like 10, 100, 1000 i.e., to the powers of 10. The procedure of multiplication using the Nikhilam involves minimum number of steps, space, time saving and only mental calculation. The numbers taken can be either less or more than the base considered. The difference between the number and the base is termed as a deviation. Deviation may be positive or negative. Positive deviation is written without the positive sign and the negative deviation is written using Rekhank (a bar on the number). Now, observe Table 2.

The general form of the multiplication under Nikhilam can be shown as follows:

Let N₁ and N₂ be the two numbers near to a given base in powers of 10, and D₁ and D₂ are their respective deviations from the base. Then N₁ X N₂ can be represented as,

Example: What is 108 x 109 in 5 seconds? (Dhaval Bhatia [2] & Aditi Singhal [3])

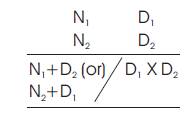
Sol: In Base 100, both numbers exceed the Base by 8 and 9 respectively.

Add 8 to the 109, giving 117 / _ _

which gives us half the answer.

Then tag on the multiplication of those two excesses,

which is 8 x 9 = 72.

Thus the mental answer is 117 / 72 or 11,772

It is brilliant and simple.

There has been a never-ending and exhausting campaign for the India- wide diffusion of all this scientific knowledge, by means of lectures, black-board demonstrations, regular classes and so on in schools, colleges, universities, etc. all over the country and have been astounding the audiences everywhere with the wonders and miracles of Indian Vedic Mathematics ( Rajesh kumar Thakur [7]).

In this connection, it is a gratifying fact that unlike so called Ideologists, there have been some great modern mathematicians and historians of Mathematics like Halstead, Ginsburg, De Moregan, Hutton, etc. who have, as truth seekers and truth-lovers, evinced a truly scientific attitude and frankly expressed their intense and whole-hearted appreciation of ancient India's grand and glorious contributions to the progress of mathematical knowledge.

The following few excerpts from the published writings of some universally acknowledged authorities in the domain of the history of mathematics, will speak eloquently for themselves:

• Halstead has quoted “the importance of the creation of Zero mark can never be exaggerated. This giving of airy nothing not merely a local habitation and a name, a picture but helpful power is the characteristic of the Hindu race whence it sprang. It is like coining the nirvana into dynamos. No single mathematical creation has been more potent for the general on-go of intelligence and power” on page 20 of his book named “On the foundation and Technique of Arithmetic”.
• Dutta says “ the Hindus adopted the decimal scale very early. The numerical language of no other nation is so scientific and has attained as high a state of perfection as that of the ancient Hindus. In symbolism, they succeeded with 10 signs to express any number most elegantly and simply. It is this beauty of the Hindu, numerical notation which attracted the attention of all the civilised people of the world and charmed them to adapt it.

 

The brain is a mental muscle and needs to be exercised. No more calculators which make the brain lazy. If we continue to teach children with an over-emphasis of using calculators in the class- room, over a 20 year period, then no doubt, the Global Brain will deteriorate. The ease and simplicity of Vedic Mathematics make the pupil invent their own methods developing creativity which leads to improved memory and greater mental agility and this in turn leads to growth in other subjects. Every person in the world irrespective of the field they are working in, needs to work with the numbers whether in employment, business or agriculture. Hence, it is necessary for everyone to have knowledge in Vedic sutras which makes their work easier and quicker. Let us promote the Vedic Mathematics through different means and encourage everyone to expertise in the Vedic sutras.