Fruit fly algorithm is a novel perspicacious optimization algorithm predicated on the foraging comportment of the authentic fruit flies. Recently, an incipient Fruit Fly Optimization Algorithm (FOA) has been proposed to solve optimization quandaries. In order to find optimum solution for an optimization quandary, fine-tuned parameters are obtained as a result of manual test in the fruit fly algorithm. This study deals with enhancing the probing efficiency and greatly ameliorate the probing quality and also on an automated approach for finding the cognate parameter by utilizing a grid search algorithm. Also it provides better ecumenical probing ability, more expeditious convergence, and more precise convergence. The optimization of a sizably voluminous antenna array for maximum directivity, utilizing a modified fruit fly optimization algorithm with desultory search of two groups of swarm and adaptive fruit fly swarm population size.
Intelligent optimization algorithms are attracting the attention of many scholars in the recent years. The Fruit fly Optimization Algorithm is introduced by Wen Tsao Pan [10]. The algorithm is originated from foraging behavior of fruit flies. The algorithm can be easily understandable because of its simple structure. Its updating strategy, which used to find the best solution, is simpler than other algorithms. However, manually definition of this update strategy causes a disadvantage. Evolutionar y computation is a shared noun, referring to "the survival of the fittest and the elimination of the unfit" of the Darwinian Theory [1], in this concept the evolutionary process of nature is practically simulated to establish computing modes, such as, the Genetic Algorithms of Holland in the early stages. However, more recently, the core of evolution began to be diverted to animal foraging behavior and group behavior, such as the Particle Swarm Optimization (PSO) by Eberhart and the Artificial Fish Swarm Algorithm (AFSA) proposed by Li of Chinese Mainland [2,6,7]. The application is part of a research method, without any restrictions on the field, it covered various fields of military, engineering, medicine, management, finance and so on. In addition, they can be combined with other data mining techniques which are used together, such as decision trees, Bayesian theorem, fuzzy math, gray system and neural network, and so on. Therefore, the use of highly flexible elastic, readers may need to be applied in accordance with their different areas, can be mixed with different algorithms. In order to investigate, whether the investors' holdings and the stocks they are going to invest will face any risks, an American scholar, Altman proposed the Z-SCORE financial warning model for the people to examine. Modified Fruit Fly Optimization Algorithm (MFOA) was proposed for the unpredictable phenomenon and process analysis [9-12]. The chaotic process is a deterministic process, but it looks chaotic and random. Studies of these chaotic behavior arises from the mathematics and pure sciences, after being cited in economics and finance. In these areas, the people want to know the existence of certain natural phenomena has not yet been recognized laws, which inspired the people for a chaos research. Scientists have noticed that, certain phenomena, such as planetary motion, there is a stable law, but others, like the weather, it is capricious. Therefore, the key question is whether the weather phenomenon is random [13-15]. Once thought to be random, and later proved to be chaotic, this issue has stimulated people to explore the truth of enthusiasm. This time, the path is generated by a deterministic nonlinear equation. Chaos theory has the following features:
It is a new method for deducing global optimization based on the foraging behavior of the fruit fly. The sensory perception of the fruit fly is better than that of other species, especially the sense of smell and vision. The olfactory organ of a fruit fly can gather various smells from the air, and even a food source 40km away. Afterwards, the fruit fly flies in the food, uses its acute vision to find the food and where its fellows gather, and then it flies in that direction, as shown in Figure 1.
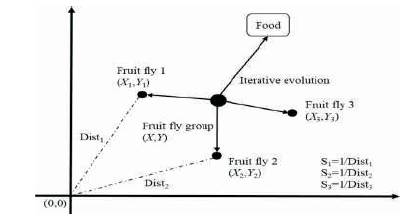
Figure 1. Schematic Diagram of Iterative Search for Food of Fruit Fly Swarm
Fruit fly characteristics of searching for food are reduced to several necessary steps and procedure [4]. The steps are described, as below:
Step 1:
The random initial position of a fruit fly swarm is shown in the right of Figure 1.
Init X_axis; Init Y_axis
Step 2:
Random direction and distance of searching for food using the sense of smell of a fruit fly individual.
Xi = X_axis + Random Value
Yi = Y_axis + Random Value
Step 3:
As the location of food cannot be known, the distance (Dist) to the origin is estimated before the decision value of smell concentration (S) is calculated; this value is the reciprocal of distance.
Step 4:
The smell concentration, decision value (S) is substituted in the smell concentration, decision function (also known as the Fitness function) to work out the smell concentration (Smell ) in the position of the fruit fly individual.
Smelli = Function (Si)
Step 5:
Determine the fruit fly with the maximum smell concentration among the fruit fly swarm (seek for the maximum value).
[bestSmell bestIndex] = max (Smell)
Step 6:
Retain the best smell concentration value and x, y coordinates. Here the fruit fly swarm flies toward the position by vision.
Smellbest = bestSmell
X_axis = X (bestIndex)
Y_axis = Y (bestIndex)
Step 7:
Enter into iterative optimization, repeat execution steps 2- 5, and judge whether the smell concentration is better than the previous iterative smell concentration, if yes, execute Step 6.
The parameter selection based on the fruit fly optimization for optimization problem [5] is as follows,
Step 1:
The main parameters of LGMS-FOA are the maximum iteration number (maxgen′), the population size (sizepop′), the searching coefficient (n), the initial weight (wo ), and the weight coefficient (α).
Step 2:
Linear generation mechanism of candidate solution.
Step 2.1:
Initial fruit fly swarm location:
x_axis’ = n * rand (domain of definition)
Step 2.2:
Give the random direction and distance for food finding of an individual fruit fly:
x’i = x_axis’ + ω * rand (domain of definition)
ω = ω0* αgen
Step 2.3:
Let the smell concentration, judgment value (Si ’) equal xj ’
S’i = x’i = x_axis’ + ω* rand (domain of definition)
Step 3:
Calculate the smell concentration (Smelli ′) of the individual fruit fly location by giving the smell concentration judgment value (S’i ) as input into the smell concentration judgment function (also called objective function):
Smelli’ = objective function (S’i)
Step 4:
Find out the fruit fly with a maximal smell concentration among the fruit fly swarm:
[Smell best’ best index’] = max(Smell’)
Step 5:
Keep the maximal concentration value and x’ coordinate. Then, the fruit fly swarm flies towards that location by using vision:
Smell best’ = best smell’,
x_axis’ = x(best index)’.
Step 6:
Enter iterative optimization to repeat the implementation of Steps 2–5. When the smell concentration is not superior to the previous iterative smell concentration any more or the iteration number reaches the maximal iteration number, the circulation stops.
LGMS-FOA can be applied into both scientific research and engineering use.
LGMS-FOA suffers from the partial optimism, which causes the less exact at the regulation of its speed and direction.
The parameter selection based on the fruit fly optimization for modified fruit fly optimization problem [6] is as follows,
Step 1:
Initiate the number of iterations (K).
Step 2:
Initiate the population size (P).
Step 3:
Randomly generates initial location of fruit fly parameters: X-axis and Y-axis.
Step 4:
Generate direction and distance for all populations (P) for the first iteration.
for i = 1 to i = P.
For group 1,
Xi = random value,
Yi = random value.
For group 2,
Xi = X-axis + random value,
Yi = Y-axis + random value.
Estimate the distance and calculate the smell concentration (S):
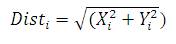
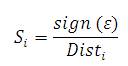
Calculate Smelli = Function (Si) and find the best smell.
Set the best smell concentration “bestSmell.”
Collect the best Xi and Yi.
End.
Step 5:
Search procedure for the second to the last iteration.
Determine the optimal random population size. Randomly assign direction and distance for all population sizes.
for i= 1 to i=P.
For group 1,
Xi = random value,
Yi = random value.
For group 2,
Xi = X-axis + random value,
Yi = Y-axis + random value.
Use the best direction and distance Xi and Yi from the previous iteration.
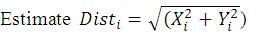
and Si = sign (ε)/Disti
Calculate Smelli = Function (Si) and find the best Smell.
If the new bestSmell is better than the old one, the bestSmell will be updated.
Set the X-axis and Y-axis into the bestSmell.
Collect the best Xi and Yi .
End.
Step 6:
Iterate for the numbers (5) until the optimum solution is met by considering a bestSmell or the last number of iterations is reached.
MFOA have no overlapping and mutation calculation. The search can be carried out by the speed of the particle.
MFOA cannot work out the problems of the noncoordination system.
The parameter selection based on the fruit fly optimization for differential evaluation problem [8] is as follows,
Step 1:
Parameters and initial population. Determine population size SizePop, iterations Maxgen, including both differential evolution scaling factor F, and crossover probability CR. Fruit fly populations location: X axis, Y axis.
Step 2:
Executive FOA algorithm processes, and documenting the best flavour concentration as Smellbest and its position:
Smellbest = bestSmell
X axis = X (bestindex)
Y axis = Y (bestindex)
Step 3:
The new fruit fly group's position is initiated by the obtained position. Performed (1) – (6) again to obtain a new flavour concentration (fitness function) and the optimal location of fruit fly.
Step 4:
Use differential operation to operate the optimal position in Step 3, the differential operation is as follows:
a) Mutation Operation: In each iteration, the authors randomly choose two different individuals based on the best position and applied to a vector of the best individual scaled, they obtain the mutated individuals.
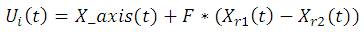
b) Cross-operation: To crossover the mutated individual and the population of individuals currently in discrete crossover manner, generating an intermediate individuals to increase the diversity of the population, the process as follows:
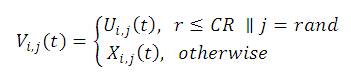
r=rand (0,1), CR ∈ [0,1] (usually 0.3)
c) Select Action: After crossing the middle of the individual with the current selection greedy individuals, compare their corresponding taste, if the current value of the individual has an excellent taste, choose it, otherwise retain, as follows:
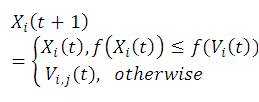
f(x) is the fitness function
Step 5:
Calculate the concentration and the smell of the position in Step 4, then compare the optimum concentration and optimum flavour of Step 3, the better value is selected (fitness function) and its location.
Step 6:
Maxgen=Maxgen+1,
Repeat Step 3–Step 5.
Step 7:
Determine whether the number of iterations is achieved, if so, end the iteration, enter the result; if not, execute Step 6.
FOADE adopts the real number code, and it is decided directly by the solution.
FOADE does not give the theoretical analysis.
The parameter selection based on the fruit fly optimization for chaotic-enhanced problem [3] are as follows,
Step 1:
Set the max iteration number k max, let k=1. Initialize fruit fly swarm location based on chaotic sequence M (•) as:
X_axisi = Li + M (·) (Ui - Li )
Y_axisi = Li + M (·) (Ui - Li )
Step 2:
Give the random direction and distance from the search of food using osphresis by an individual fruit fly as:
Xi = X_axis + R(k) * M(·)
Yi = Y_axis + R(k) * M(·)
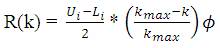
Step 3:
The distance Dist is then estimated, and the fitness i judgment value Si is calculated by:
Disti = Xi2 - Yi2
Si = Disti
Step 4:
Substitute fitness judgment value (S ) into a fitness function i so as to find the fitness function value (Smell ) of the i individual location of the fruit fly.
Smelli = Function (Si)
Step 5:
Find out the fruit fly with the minimum value or the best fitness value among the fruit fly swarm.
[bestSmell bestIndex] = min (Smell)
Step 6:
Judge if the fitness is superior to the previous iterative fitness, if so, update the best fitness value and at this moment, the fruit fly swarm will use vision to fly towards that location.
Smellbest = bestSmell
X_axis = X(bestindex)
Y_axis = Y(bestindex)
Step 7:
If k ≥ k max, stop the CFOA search; otherwise, go to Step 2.
CFOA used in dynamic applications based on the fitness value has been used in a complex manner.
CFOA is experimented that, the convergence time is uncertain.
Fruit fly algorithm is a novel perspicacious optimization algorithm predicated on the foraging comportment of the authentic fruit flies. Recently, an incipient Fruit fly Optimization Algorithm (FOA) has been proposed to solve optimization quandaries. Although Fruit fly Optimization Algorithm has many advantages, it still has the weakness of low convergence precision, and easily relapsing into local extremum, and when faced to different questions, there are big differences in their characteristics. However, there are also problems in parameter setting and practical engineering applications, along with introducing differential thought. Thus, the study of fruit fly optimization techniques for various approaches are compared with the parameter setup.