In RSA (Rivest-Shamir-Adleman) cryptography, the basic factors are key length, calculation time, security, authentication and integrity. Generally, in public key cryptography, the key length and security is directly proportional to each other. Original RSA uses two prime numbers as input, which gives the modulus 'n'; encryption and decryption process depends on modulus 'n'. The attacker can easily break the 'n' into two factors of prime number and so to avoid this problem, the authors have used three large prime numbers, it will increase the brute force time to factorize 'n'. This paper mainly focuses on the number of prime numbers used, security and time.
Cryptography is playing a major role in data protection applications running in a network environment. It allows people to do business electronically, without worries of deceit and deception in addition to ensuring the integrity of the message and authenticity of the sender [26]. It has become more critical to our day-to-day life because thousands of people interact electronically every day; through e-mail, e-commerce, ATM machines, cellular phones, etc, [1], [3]. The development of public-key cryptography has enabled large-scale network of users that can communicate securely with one another even if they had never communicated before. This paper considers a Public Key encryption method using RSA algorithm that will convert the information into a form not understandable by the intruder, therefore protecting the unauthorized users from having access to the information even if they are able to break into the system [8], [25].
Cryptography is defined from two Greek words Crypto and Graphy; Crypto means Hidden and Graphy means writing. It is the study of techniques for secure communication in the presence of third party [4], [28]. Figure 1 shows the description of cryptography.
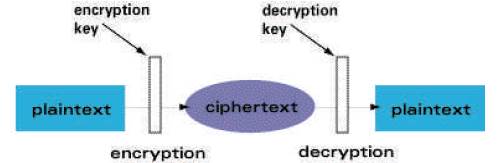
Figure 1. Basic Diagram for Cryptography
Cryptography is basically classified in to two types -
Figure 2 describes the types of cryptography on the basis of key.

Figure 2. Classification of Cryptography
Symmetric-key algorithms use the same cryptographic keys for both encryption of the plain text and decryption of the cipher text as shown in Figure 3 [27], [28]. The keys may be identical or there may be a simple transformation to go between the two keys.

Figure 3. Symmetric Key Cryptography
Asymmetric cryptography or public-key cryptography is a cryptography in which, a pair of keys is used to encrypt and decrypt a message so that, it arrives securely as shown in Figure 4 [27]. Initially, a network user receives a public and private key pair from a certificate authority.
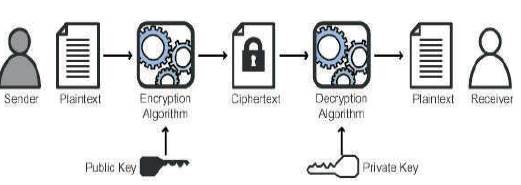
Figure 4. Asymmetric Key Cryptograph
Sarika Khatarkar and Rachana Kamble [2] have studied many different asymmetric cryptography techniques and analyzed with different techniques. Also RSA based encryption techniques are compared, to give the advantages and disadvantages of RSA algorithm.
Joshi Maitri and Fenil Khatiwala [3] have studied on public key generation, RSA algorithm and various improved algorithm by applying various modifications on the existing algorithms and represents the summarized results through different open sources.
Gaurav Patel, Krunal Panchal and Sarthak Patel[30] have surveyed various modification approaches applied to the RSA algorithm in order to enhance it. The main disadvantage of RSA cryptography is the computational time, so many researchers apply various methods to improve the speed of RSA algorithm.
Ravi Shankar Dhakar and Amit Kumar Gupta[13] have presented a new cryptographic algorithm based on Additive Homomorphic properties called Modified RSA Encryption Algorithm (MERA). In this proposed algorithm, two pairs of different keys are used. The mathematical attack and problems of trying all possible private keys has brute force attack which can be improved by MERA algorithm.
Persis Urbana Ivy, Purshotam Mandiwa and Mukesh Kumar [1] have proposed the RSA with 'n' prime numbers, which provide better security in the network. It is implemented by four prime numbers; if large prime numbers are used, then it is not breakable. But if cryptanalyst factories the 'n' then easily the algorithm lock can be opened.
Xin Zhou and Xiaofei Tang [16] have discussed and implemented the encryption and decryption with RSA algorithm in detail. Also the RSA algorithm with digital signature and other related technology plays an important role for the communication purpose.
RSA was first described in 1977 by Ron Rivest, Adi Shamir and Leonard Adleman of the Massachusetts Institute of Technology [18], [28]. RSA includes the public and private key. The public key is only used to encrypt the messages and it can be seen to all [22]. The private key is used to decrypt the messages. Private Key is also called as the secret key [5], [6], [7], [14].
It is the process of converting the plain text into cipher text; the mathematical calculation is given by,
C=Me mod n
where, M is the original message i.e. plaintext and C is the cipher text[9], [12].
The reverse process of encryption is called decryption; converting the cipher text to plain text [11], [15]. Figure 5 describes the flowchart of RSA algorithm.
M=Cd mod n
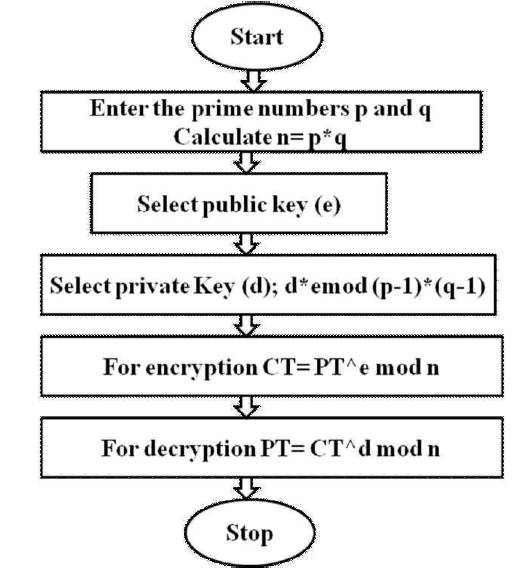
Figure 5. Flowchart of RSA Algorithm
RSA algorithm is basically based on the prime numbers and 'n'[17], [19]. Brute force attack and the time taken for the attack is totally dependent on the factorization of 'n' [21]. Traditional RSA use only two prime numbers (p and q); as 'n' is the modulus that is made public and length of 'n' is considered as the length of key in the RSA cryptography [13].
Encryption and Decryption process is same as the original RSA cryptography [23]. Figure 6 describes the process of the proposed algorithm.
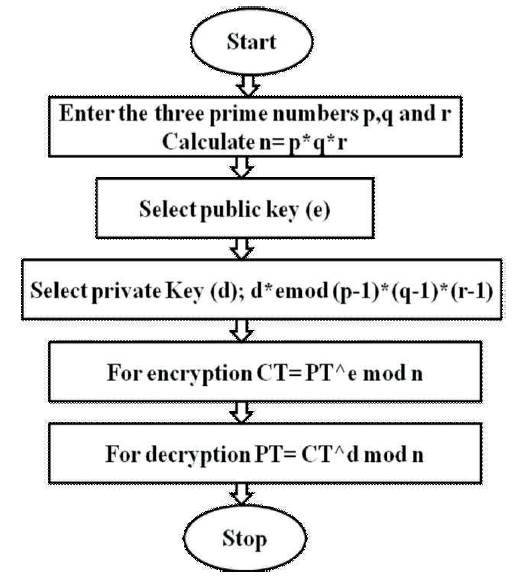
Figure 6. Flowchart of Proposed Algorithm
The original RSA and the proposed algorithm are implemented in MATLAB R2013a successfully. Figure 7 describes the input of the original RSA algorithm. According to the algorithm, the public key and private key are calculated, with the use of those keys, encryption and decryption process are performed as shown in Figure 8.
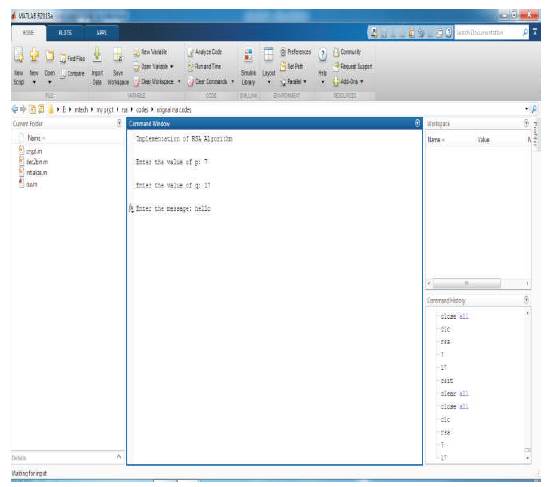
Figure 7. Input of Original RSA Algorithm
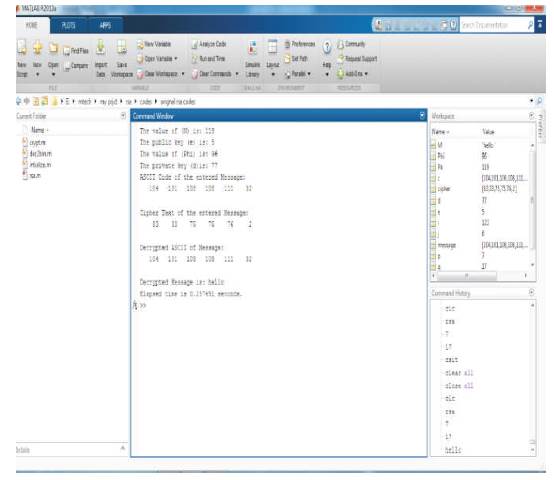
Figure 8. Output of Original RSA Algorithm
Figure 9 shows the input for the proposed algorithm. According to that algorithm, keys are generated and encryption and decryption process are performed successfully as it is shown in Figure 10.
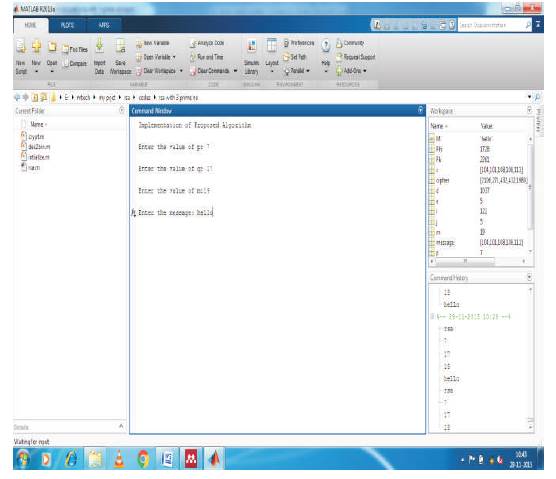
Figure 9. Input of Proposed Algorithm
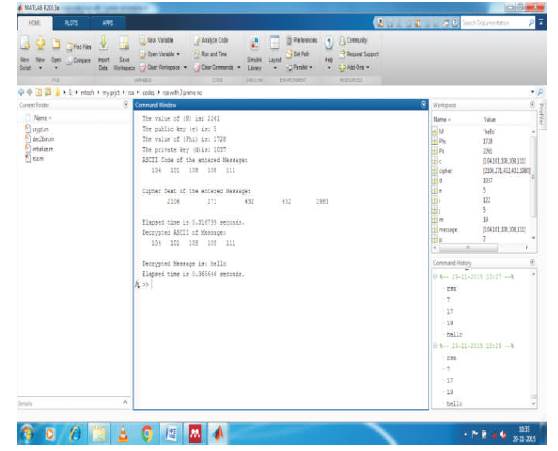
Figure 10. Output of Proposed Algorithm
The total time taken for key generation, encryption and decryption is more in the proposed algorithm, as compared to the original RSA. Also the length of the key is large in the proposed work. In public key cryptography, the large size of key length provides more security to the algorithm, such that the proposed work provides more security and authentication to the user [19], [24].
From the above performed experiment, results are compared with respect to their execution time and the prime numbers are used as it is briefly described in Table 1.

Table 1. Comparison of RSA and Proposed Algorithm
In this paper, the original RSA algorithm and the proposed algorithm is implemented in MATLAB R2013a. Both the algorithms are compared in terms of security, time and the number of prime numbers used in it. The proposed method is a modification of the RSA algorithm. In this paper, only few concepts were modified further, RSA can be modified with many logical change in mathematical calculation and also, it can be merged with Diffie-Hellman key exchange and Digital signature. However, RSA is mostly applied in text data, it can be further implemented in image, video, etc.