References
[1]. D. A. Brannan and J. G. Clunie, (1980). “Aspects of Contemporary Complex Analysis”, Proceedings of the NATO
Advanced Study Institute.
[2]. J. Dziok and H. M. Srivastava, (1999). “Classes of Analytic Functions Associated with the Generalized Hyper Geometric
Function”, Applied Mathematics and Computation, Vol.103, pp.1-13.
[3]. J. Dziok and H. M. Srivastava, (2003). “Certain Subclasses of Analytic Functions Associated with the Generalized Hyper
Geometric Function”, Integral Transforms Specification Function, Vol.14, pp.7-18.
[4]. R. W. Ibrahim and M. Darus, ( 2011). “On Operator by Double Zeta Functions”, Tamkang Journal of Mathematics,
Vol.42(2), pp.163-174.
[5]. V. Kiryakova, (1993). “Generalized Fractional Calculus and Applications”, Pitman Research Notes in Mathematics,
Vol.301.
[6]. V. Kiryakova, (2011). “Criteria for Univalence of the Dziok-Srivastava and the Srivastava-Owa Operators in the Class A”,
Applied Mathematics and Computation, Vol.218, pp.883-892.
[7]. M. Lewin, (1967). “On a Coefficient Problem for Bi-univalent Functions”, Proceedings on American Mathematics Society,
Vol.18, pp.63-68.
[8]. E. Netanyahu, (1969). “The Minimal Distance of the Image Boundary from the Origin and the Second Coefficient of a
Univalent Function in z < 1”, Archive for Rational Mechanics and Analysis, Vol. 32, pp.100-112.
[9]. CH. Pommerenke, (1975). “Univalent Functions”, Gotingen.
[10]. Saibah Siregar, Sintuja Raman, (2012). “Certain Subclasses of Analytic and Bi-univalent Functions Involving Double Zeta
Function”, International Journal on Advanced Science Engineering Information Technology, Vol.2, pp.16-18.
[11]. H. M. Srivastava, (2007). “Some Fox-Wright Generalized Hypergeometric Functions and Associated Families of
Convolution Operators”, Application, Analysis and Discrete Mathematics, Vol.1, pp.56-71.
[12]. H. M. Srivastava, S. Bulut, M. C. A Glar and N. Ya Gmur, (2013). “Coefficient Estimates for a General Subclass of Analytic
and Bi-univalent Functions”, Filomat, Vol.27, pp.831-842.
[13]. H. M. Srivastava, A. K. Mishra and P. Gochhayat, (2010). “Certain Subclasses of Analytic and Bi-Univalent Functions”,
Applied Mathematics Letters, Vol.23, pp.1188-1192.
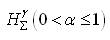 of Analytic and Biunivalent functions in the open unit disc Δ. For functions belonging to these classes, the authors have obtained estimates on the first two Taylor-Maclaurin coefficients
of Analytic and Biunivalent functions in the open unit disc Δ. For functions belonging to these classes, the authors have obtained estimates on the first two Taylor-Maclaurin coefficients 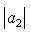 and
and 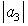 . The results of this paper will generalize some of the earlier known results.
">
. The results of this paper will generalize some of the earlier known results.
">
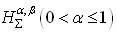 ,
,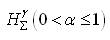 of Analytic and Biunivalent functions in the open unit disc Δ. For functions belonging to these classes, the authors have obtained estimates on the first two Taylor-Maclaurin coefficients
of Analytic and Biunivalent functions in the open unit disc Δ. For functions belonging to these classes, the authors have obtained estimates on the first two Taylor-Maclaurin coefficients 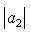 and
and 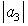 . The results of this paper will generalize some of the earlier known results.
. The results of this paper will generalize some of the earlier known results.