References
[1]. Bequette B. W, (2003). “Process Control: Modeling,
Design and Simulation”, Prentice Hall, India.
[2]. Chidambaram M., (1997). “Control of Unstable Systems:
A Review”, Journal of Energy, Heat and Mass Transfer, Vol. 19,
pp. 49-57.
[3]. Chidambaram M and R. Padma Sree, (2003). “A
Simple Method of Designing PI / PID Controllers for
Integrator/Dead Time Processes”, Computer and
Chemical Engineering, Vol . 27, pp. 211-215.
[4]. Cho W., Lee J., and Edgar T. F, (2014). “Simple Analytic
Proportional-Integral-Derivative (PID) Controller Tuning Rules
for Unstable Processes”, Industrial and Engineering
Chemistry Research, Vol. 53, pp. 5048-5054.
[5]. Huang H. P and C. C. Chen, (1999). “Auto Tuning of PID
Controllers for Second Order Unstable Systems Having
Dead Time”, Journal on Chemical Engineering, Vol.32, pp.
568-579.
[6]. Marlin T. E., (1995). “Process Control: Designing
Processes and Control Systems for Dynamic
Performance”, McGraw- Hill, New York.
[7]. Nasution A. A, J. C Jung, and H. P Huang., (2011).
2 “Optimal H IMC-PID Controller with Set Point Weighting for
Time Delayed Unstable Processes”, Industrial and
Engineering Chemistry Research, Vol. 50, pp. 4567-4578.
[8]. Jacobsen E. W., (1999). “On the Dynamics of
Integrated Plants Non-minimum Phase Behavior”, Journal
on Process Control, Vol. 9, pp. 439-451.
[9]. Krishna D, K. Suryanarayana, G. Aparna and R.
Padma Sree, (2012). “Tuning of PID controllers for Unstable
Stirred Tank Reactors”, International Journal of Applied
Science and Engineering, Vol.10, pp. 1-18.
[10]. Lee Y, J. Lee and S. Park, (2000). “PID Controller
Tuning for Integrating and Unstable Processes with Time
Delay”, Chemical Engineering Science, Vol. 55, pp.3481-
3493.
[11]. Padma Sree R. and M. Chidambaram, (2003). “IMC
Controller Design for Unstable with a Zero”, Proceedings of
International Conference on Chemical and Bio-chemical
Engineering, pp. 843-850.
[12]. Padma Sree R. and M. Chidambaram, (2004a).
“Control of Unstable Reactor with an Unstable Zero”, Indian
Chemical Engineering, Vol. 46, pp. 21-26.
[13]. Padma Sree, R., M.N. Srinivas and M. Chidambaram, (2004b). “A Simple Method of Tuning PID Controllers for
Stable and Unstable FOPTD Systems”, Computer and
Chemical Engineering, Vol. 28, pp. 2201-2218.
[14]. Padma Sree, R. and M. Chidambaram, (2004c).
“Simple Method of Calculating Set Point Weighting
Parameter for Unstable Systems with a Zero”, Computer
and Chemical Engineering, Vol. 28, PP. 2433-2437
[15]. Padma Sree R and M. Chidambaram, (2005). “Simple
and Robust Method of Tuning PID Controller for Integrator/
Dead Time Process”, Journal of Chemical Engineering, Vol.
38, pp .113-119.
[16]. Padma Sree R. and M. Chidambaram, (2006).
“Control of Unstable Systems”, Narosa Publishing House,
New Delhi.
[17]. Seborg D. E., T. F. Edgar and D. A. Mellichamp, (2004).
“Process Dynamics and Control”, John Wiley and Sons, New
York.
[18]. Seki H., M. Ogawa and M. Ohshima, (2001). “PID
Temperature Control of an Unstable Gas –phase Polyolefin
Reactor”, Journal on Chemical Engineering, Vol. 34, pp.
1415-1422.
[19]. Seshagiri Rao A. and M. Chidambaram, (2007).
“Control of unstable Processes with Two RHP Poles, a Zero
and Time Delay”, Asia-Pacific Journal of Chemical
Engineering, Vol. 1 ,No.1-2, pp. 63-69.
[20]. Seshagiri Rao, A and M. Chidambaram, (2006).
“Enhanced Two-Degrees-of-Freedom Control Strategy for
Second-Order Unstable Processes with Time Delay”,
Industrial and Engineering Chemistry Research, Vol. 45,
pp. 3604-3614.
[21]. Shamsuzzoha M and M. Lee, (2007). “Analytical
Controller Design of Integrating and First Order Unstable
th Time Delay Process”, 8 International IFAC Symposium on
Dynamics and Control of Process Systems, Vol.2, pp. 397-
402.
[22]. Shamsuzzoha M. and M. Lee, (2008a). “Design of
Advanced PID Controller for Enhanced Disturbance
Rejection of Second-order Processes with Time Delay”,
AIChE Journal, Vol. 54, pp. 1526 .
[23]. Shamsuzzoha M. and M. Lee, (2008b). “Analytical
Design of Enhanced PID Filter Controller for Integrating and
First Order Unstable Processes with Time Delay”, Chemical
Engineering and Science, Vol. 63, pp. 2717.
[24]. Shamsuzzoha M. and M. Lee, (2009). “Enhanced
Disturbance Rejection for Open-loop Unstable Process with
Time Delay”, ISA Transactions, Vol. 48, pp. 237-244.
[25]. Wang Y.J., (2014). “Determination of all Feasible
Robust PID Controllers for Open-loop Unstable Plus Time
Delay Processes with Gain Margin and Phase Margin
Specifications”, ISA Transactions, Vol. 53, pp. 628–646.
[26]. Wang L.W. and S.H. Hwang, (2005). “Identification
and Control of Unstable Processes of Three Dynamic
Types”, Chemical Engineering and Communication, Vol.
192,No.1, pp. 34-61.
[27]. Vu T.L.U and M.A. Lee, (2013). “A Unified Approach to
the Design of Advanced Proportional-Integral-Derivative
Controllers for Time-delay Processes”, Korean Journal on
Chemical Engineering, Vol. 30, No.3, pp. 546-558.
[28]. Vanavil B., K. Krishna Chaitanya and A. Seshagiri
Rao, (2013). “Improved PID Controller Design for Unstable
Time Delay Processes Based on Direct Synthesis Method
and Maximum Sensitivity”, International Journal of Systems
Science, pp.1-17.
[29]. Vanavil B., A. V. N. L. Anusha, M. Perumalsamy and A.
Seshagiri Rao, (2014). “Enhanced IMC-PID Controller
Design with Lead-Lag Filter for Unstable and Integrating
Processes with Time Delay”, Chemical Engineering and
Communication, Vol. 201, pp. 1468–1496.
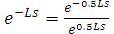and it is expanded using Taylor series expansion upto four terms both in the numerator and denominator.This makes the numerator and denominator as polynomial of s. The time delay term in the numerator shifts the response on time axis and is not considered in the design problem. By equating the corresponding coefficients of s, s2 and s3 in the numerator with α1 , α2 , and α3 times that of the denominator; three linear equations are formulated and solved for the PID controller parameters. In the proposed work, the coefficients α1 , α2 , and α3 are obtained by minimizing Integral Time weighted Absolute Error (ITAE) for servo problem using fminunc of Matlab. Simulation results on various transfer function models and on the nonlinear model equations of jacketed CSTR (Continuous Stirred Tank Reactor) carrying out first order exothermic reaction are given to demonstrate the effectiveness of the proposed method. The smooth functioning of the controller is expressed interms of total variation. The controller performance is expressed in terms of ITAE. Nominal control performance of the proposed method is better than the existing methods.
