References
[1]. R.P. Agarwal, Maria Meehan and Donal O’Regan, (2001). Fixed point theory and applications, Cambridge tracts in
mathematics.
[2]. J.P. Aubin and A. Cellina, (1984). Differential Inclusions, Springer-Verlag.
[3]. T. Cardinali, K. Nikodem and F. Papalini, (1993). Some results on stability and characterization of k-convexity of setvalued
functions, Ann. Polon, Math. 58, 185-192.
[4]. V.V. Chistyakov and A. Nowak, (2005). Regular Caratheodory-type selectors under no convexity assumptions, Journal of
Functional Analysis, 225, 247-262.
[5]. A.M.A. El-sayed and A.G. Ibrahim, (1995). Multivalued fractional differential equations, Applied Mathematics and
Computation, 68, 15-25.
[6]. A.M.A. El-sayed and Yassine Khouni, (2012). Measurable-Lipschitz selections and set-valued integral equations of
fractional order, 2, 1-8.
[7]. R. W. Ibrahim, (2009). Existence of convex and non convex local solutions for fractional differential inclusions, 18, 1-13.
[8]. K. Nikodem, (1984). On quadratic set-valued functions, Publ. Math. Debrecen 30, 297-301.
[9]. K. Nikodem, (1987). On jensen’s functional equation for set-valued functions, Rad. Math 3, 23-33.
[10]. K. Nikodem, (1988). Set-valued solutions of the pexider functional equations, Funkcial.Ekvac 31(1988), 227-231.
[11]. D. Popa, (2004). Functional inclusions on square symmetric grupoids and Hyers-Ulam stability, Mathematical Inequal &
Appl. 7, 419-428.
[12]. D. Popa, (2009). Aproperty of a functional inclusion connected with Hyers-Ulam stability. J. Math. Inequal, 4, 591-598.
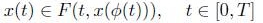in the two classes C[0, T] and L1 [0, T].
