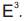 We obtain the curvatures, the Christoffel symbols and the shape operator of this inverse surface by the help of these of the tangent developable surface. Morever, we give some necessary and sufficient conditions regarding the inverse surface being flat and minimal.
">
We obtain the curvatures, the Christoffel symbols and the shape operator of this inverse surface by the help of these of the tangent developable surface. Morever, we give some necessary and sufficient conditions regarding the inverse surface being flat and minimal.
">
In this paper, we define the inverse surface of a tangent developable surface with respect to the sphere Sc(r) with the center 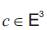 and the radius r in 3-dimensional Euclidean space
and the radius r in 3-dimensional Euclidean space 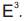 We obtain the curvatures, the Christoffel symbols and the shape operator of this inverse surface by the help of these of the tangent developable surface. Morever, we give some necessary and sufficient conditions regarding the inverse surface being flat and minimal.
We obtain the curvatures, the Christoffel symbols and the shape operator of this inverse surface by the help of these of the tangent developable surface. Morever, we give some necessary and sufficient conditions regarding the inverse surface being flat and minimal.