At the heart of the Capital Asset Pricing Model (CAPM) lies the concept of systematic risk. The systematic risk of a security is that component of the total risk of the security that is explained by market risk. This is captured through the regression of security returns r_t on market returns r_Mt , viz

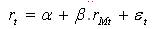
The regression coefficient β(r) measures the sensitivity of returns of the security to changes in market returns.

From an econometric perspective, two concepts become relevant in this context. Firstly, in order for the above regression to be meaningful, the time series {r_t} and {r_Mt} should be stationary. In particular, the presence of a unit root would undermine the significance of β(r), and therefore threaten the entire basis of the CAPM. Secondly, there should be some form of causality from changes in market returns to changes in security returns. In particular, Granger causality from market returns to security returns must hold.

It is in this context that stationarity and Granger causality should be examined for the security line, as represented by the above regression. As Soufian (2001) has pointed out, in order for the regression analyses used for CAPM and APT (Arbitrage Pricing Theory) tests to be meaningful, it is essential to identify the processes that generate the series. In particular, Granger causality may offer an approach to determining the macroeconomic variables that influence asset returns in general.