Low Power and Area Efficient FFT Processor using Radix-24 Feed Forward Multipath Delay Commutator for Wireless Communication

C. Padma *  P. Jagadamba **  P. Ramana Reddy ***
*,*** Department of Electronics and Communication Engineering, Jawaharlal Nehru Technological University, Ananthapuramu, Andhra Pradesh, India.
** Department of Electronics and Communication Engineering, Srikalahasthi Institute of Technology, Srikalahasti, Andhra Pradesh, India.

Abstract

Radix-2k delay feed-back and radix-K delay commutator are the most well-known pipeline architecture for FFT design. The radix-2k fast Fourier transform algorithm is employed to achieve low power at the same time a radix-2 FFT algorithm reduced number of twiddle factor multiplication it reduces the area. This article describes a novel radix-24 multiple delay commutators called 4 - path feed forward FFT architecture utilizing the advantages of the radix-2 algorithm, such as simple butterflies and less memory requirement. Therefore, it is more efficient in terms of hardware and higher throughput by implementing parallelism and multiple delay commutator. Combining benefits of both radix-2 algorithm and feed forward architecture, the proposed 4-path radix-24 FFT processor achieves the lowest hardware requirements for multipliers which is 20% lesser and power consumption which reduces more than 30% when compared with dual path radix-22  and radix-24 delay feedback FFT architecture. The entire FFT algorithms were implemented in Verilog hardware description language and synthesized with 90 nm Technology Libraries using Cadence RTL Compiler

Keywords :

Introduction

The Fourier transform (FT) is a technique to transform a signal from the time domain into the frequency domain to analyze the signal's frequency components. Within the frequency domain, the absolute value at each frequency represents its contributing amount to the original signal while the complex value explains the phase offset of the sinusoid at that frequency. Since 1960, many research works have been carried out to calculate the Fourier transform at improved speed and contributed to the Fast Fourier transform (FFT). Various FFT algorithms have been reported such as Cooley-Tukey ( Heideman, et al., 1984), Prime-factor ( Jiang et al., 2012), Brunn ( Mittal et al., 2007), and Hexagonal ( Birdsong & Rummelt, 2016) FFTs. The Fast Fourier transform is one of the important and widely used functions in the field of ( Padma et al., 2020) digital signal processing (DSP) and image processing. Pipelined architectures are largely preferred for FFT computations as these provide higher throughput, low latency, and low area and decreased power consumption. It is critical to use a suitable hardware structure that has the potential to meet such requirements.

Single-path pipelined structures are useful for high-speed, real-time applications that have a sequential input/output data. Most of the transforms require global data inter connections, which calls for parallel hardware structures. However, the parallel structures typically use many arithmetic units in hardware, which leads to a large chip area and high power consumption. To generate higher throughput, more processing paths can be implemented in parallel at the cost of additional hardware and power. For FFT processors, Chen et al. (2008) used a multiple input, multiple output (MIMO) scheme and dynamic voltage and frequency scaling (DVFS). It could operate at 300 MHz with the throughput of up to 2.4 G sample/s by consuming 119.7 mW at 0.85 V supply. To reduce power consumption, Wang and Chandrakasan (2005) were proposed A superpipeline FFT cores demonstrated sub-threshold FFT designs using optimal energy points and optimal pipeline techniques. However, Radix-4 multiple delay commutator (MDC) was proposed by Jeon et al. (2011) using the FFT processor architecture, which requires a larger memory size. Since the size of the memory is proportional to the level of parallelism, higher the level of parallelism will increase the hardware area and the power linearly. Therefore, more hardware and power efficient parallel architecture needs to be developed.

The most widely used FFT is the Cooley-Tukey algorithm ( Mangaiyarkarasi & Paul, 2014). This is a divide and conquer algorithm that recursively breaks down a DFT of any composite size N into many smaller DFTs of sizes along side O(N) multiplications with twiddle factors. This algorithm employs decimation-in-time (DIT).Frequency- based (DIF) Fast Fourier Transform. DIT FFT orders the info from bit reversal to normal order, where as DIF FFT converse. The elemental idea of those algorithms are that the N point FFT is divided into smaller and smaller parts until only two points FFT. Hence this can be called as Radix-2 algorithm. This paper analyses the realization of the 128 points FFT where we design a Radix-24 algorithm with dual path feed forward FFT and a 4-path Feed forward FFT with Radix-24 algorithm in which we got better results at 4-Path FFT technique when compared to Dual feed forward Radix-2, Radix-22 and Radix 24 algorithms( Chen & Chen, 2013).

The reminder of the paper is organized as follows,

In Section II we discuss about the Earlier FFT algorithms in Section III we discuss about the radix-22 FFT algorithms and In Section IV we presented our proposed work of Radix-24 FFT algorithm with modified Structure. In section V we have Results and Discussion and finally in Section VI we conclude the paper.

1. Fast Fourier Transform (FFT)

The Discrete Fourier Transform (DFT) is a powerful computation tool which allows us to evaluate the Fourier Transform X(ejw) on a digital computer or specially designed hardware. Unlike DTFT, which is defined for finite and infinite sequences, DFT is designed only for finite length. The discrete Fourier transform (DFT) has seen wide usage across a larger number of fields. It is extensively used in data compression, radar, image processing, voice processing, communications, GPS navigation and sonar systems ( Mohapatra & Mohapatra, 2017). All applications of the DFT depend crucially on the supply of a quick algorithm to compute discrete Fourier transform and their inverses. Apart from defining the frequency content of a signal, DFT is used to perform linear filtering operations in the frequency domain.

The fast Fourier transform is an efficient algorithm to work out the discrete Fourier transform and its inverse. It generates the same accurately as evaluating the DFT definition directly; the only difference is that FFT is much faster. The foremost common FFT is that the Cooley-Tukey algorithm. The fundamental idea of these FFT algorithms is decomposition and breaking the transform into lesser and smaller parts and mixing them to urge the entire transform. FFT decreases the computation time required to compute a discrete Fourier transform and increases the performance factor by 100.

The Discrete Fourier Transform (DFT) of a sequence u(n), n = 0,1,2,….N - 1 is defined as

(1)

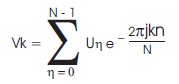
where, k= 0, 1, 2…N-1

If

(2)

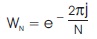
Then Vk is defined as

(3)

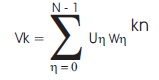
2-D DFT has an application in image and video processing. The Two-Dimensional DFT of an N x N image u(m,n) is a separable transform defined as

(4)

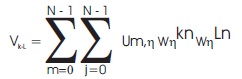
1.1 FFT Algorithms

In FFT, a N-point ( Padma et al., 2018) discrete time signal x[n] can be represented within the frequency domain in the form of below equation by (1):

(5)

where is called a twiddle factor.

Equation (6) can be further decomposed into Equations (7) to (9) to have radix-2 as discussed in the following sections.

1.2 Radix-2 FFT Algorithm

The radix-2 FFT algorithm is obtained by using the divideand- conquer approach ( Mookherjee et al., 2015). If the output sequence X(k) is divided into two summations, one of which involves the addition over the first 2/ N data points and the second involves the addition of the last 2/ N data points.

(6)

k = 0,1,2 ... ..., N – 1

Let k = 2m and k = 2m +1 (m = 0, 1,...., N/2-1),

we have,

(7)

which is a N/2 point FFT of 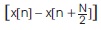and

(8)

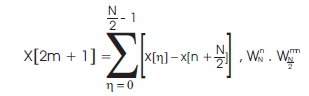
which is a N/2 point FFT of 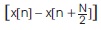respectively.

N-point FFT is obtained by iterating the procedure in Equation (8) and (9) over log2 (N-1) times. This reduces the number of operations and hardware implementation cost (multipliers and adders).

The Figure 1 shown below is the radix-2 decimation-infrequency FFT of 8-point. In the DIF algorithm, the decimation is finished in the frequency domain. That is the reason, the frequency indices are in bit-reversed order. Here start with a single 8-point DFT, progress on to two 4-point DFTs and completed with four 2-point DFTs.

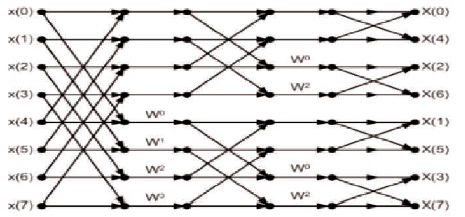
Figure 1. FFT Algorithm of 8-Point Radix-2 with Decimation-in-Frequency

1.3 Radix-2 FFT Algorithms

As Classic FFT algorithms include radix-2 algorithm, radix-4 algorithm with decimation in time (DIT) or decimation in frequency (DIF) butterfly operation, etc. It is derived from the above formula that Radix-22 algorithm has the similar multiplication complexity with radix-4 algorithm (Chen et al., 2015), but retains the realization structure of radix-2 algorithm. The major improvement is to decompose the radix-4 butterfly unit into two radix-2 butterfly unit, which combines the advantages of both Radix-2 Serial Delay Feedback and radix-4 Serial Delay Feedback structure. This structure has simple control logic, high utilization of the butterfly unit and low cost of memory and multiplier. With the pipelined structure it can process input data continuously, therefore is suitable for VLSI implementation.

By considering the first two decompositions of radix-2 together, Equation (6) can be written in another form as in Equation (10).

(9)

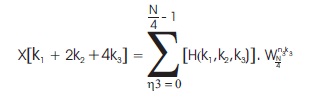
where,

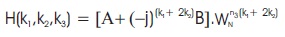
Here, A and B are two conventional radix-2 FFT and H(k1,k2,k2) is also a radix-2 FFT of A and B with an additional complex multiplier for the twiddle factor WNn3(k1+2k2). Using this decomposition, the first two stages of radix-2 can be transferred into one stage radix-22 consisting of two cascaded radix-2 FFT. The flow graph of this algorithm is depicted in Figure 2.

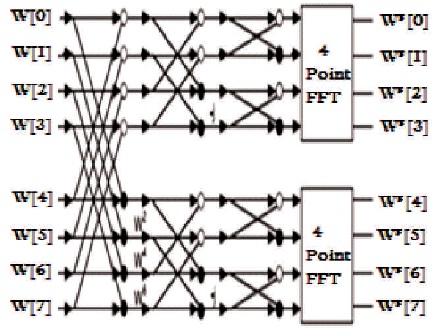
Figure 2. 8-Point Radix-22 FFT Algorithm

Radix-22 has a simple architecture of Radix-2 and has the similar number of iterated stages log 4 (N-1) as in radix-4. In terms of calculating operations and hardware implementation, radix-22 has less complex architecture with a smaller number of multipliers. Therefore, it is very popular for pipeline FFT implementation to reduce the power consumption.

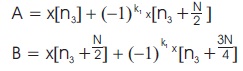
1.4 Twiddle Factor Generation

From Equation (6),

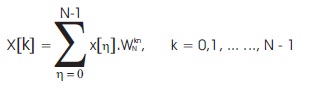
where 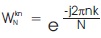is called a twiddle factor.

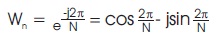
In order to understand the FFT more visually, 4 point FFT equation is converted to matrix notation in Figure 3.

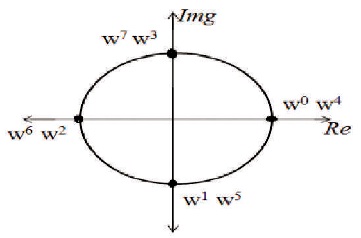
Figure 3. Twiddle Factor Representation of a 4-point FFT

Within the matrix notation, 4X4 twiddle factor matrix is given in Equation (10). The first row has all the 4 value as W0. Within the second row, twiddle factor is rotating on the circle once with clockwise direction. Within the third row, twiddle factor is rotating on the circle twice. Within the 4th row, twiddle factor is rotation on the circle once with counter-clockwise direction and this will be considered as three-time rotation with clockwise direction.

(10)

For radix-4 the twiddle factors are

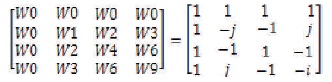
For radix - 2 the twiddle factors are

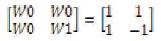
2. FFT Methodologies

2.1 Existing Radix-22 Feed-Forward FFT Processor

Figure 4 shows the architecture of a 1024 point radix-22 MDC FFT processor with two parallel data paths and seven processing stages. Here, the odd numbered processing stages execute the BF operations for calculating A and B.

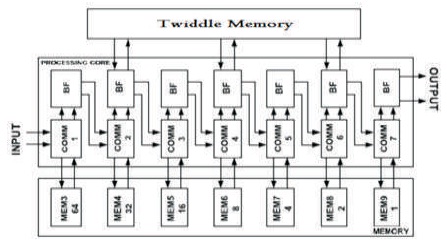
Figure 4. 128-Point Radix-22 Feed Forward FFT Architecture with Two Parallel Data Paths

A memory replaces the function of the conventional delay lines for low power and high density. Even though static random access memory (SRAM) can be a good performer, the requirement for high operating frequency (up to 500 MHz) posts a challenge in low power SRAM design. Therefore, this work employs a register based memory and SRAM implementation shall be left for a future work. By interchanging between two phases, two n-block memories are switched between the two inputs, creating a required n-distance data at the output. In comparison with the conventional input scheduler, the proposed algorithm only changes the content of one memory cell in each clock cycle since it is able to access every single cell by its address. Whereas, the conventional scheduler changes the content of all FIFOs in the delay lines for each clock cycle and consumes significant switching power, especially when long delay lines are required at the beginning stages of FFT.

2.2 Proposed Radix-24 Feed-forward Fft Processor

In this work, identical radix-24 FFT algorithms are presented. This algorithm has similar butterfly structure and data input/output sequence as radix-22 as shown in Figure 4. The difference is twiddle factor stage location in a signal flow graph except one case, where the complexity of twiddle factor multiplication is also reduced. This variation of the FFT algorithm affects the overall round-off error at output. Following the method used, we calculate the amount of non-trivial multiplications and round-off noise for analysis of similar radix-2k FFT algorithms.

As shown in Figure 5, the odd-numbered BF and the even-numbered BF are called Butterfly Type I (BFI) and Butterfly Type II (BFII), respectively. BFI is just a conventional radix-2 BF while BFII is a slightly modified radix-2 BF for realizing H in Equation (10) with complex number multipliers as shown in Figure 6. BFII requires an additional control signal (Ctrl) and multiplexers for switching data between two phases. This control signal is generated from the most significant bit (MSB) of an nbit counter where n is (1 + log2d) and d is the distance required between two BF's inputs. For example, when the input distance in the second stage is 128, an 8-bit counter is used for generating Ctrl input.

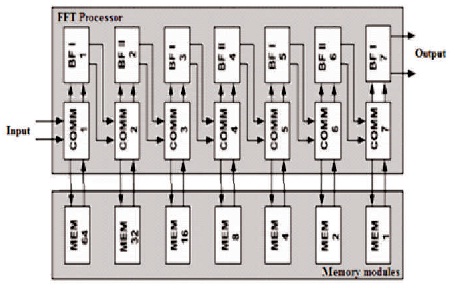
Figure 5. Proposed 128-Point Radix-24 FFT Processor with Pipelined Input

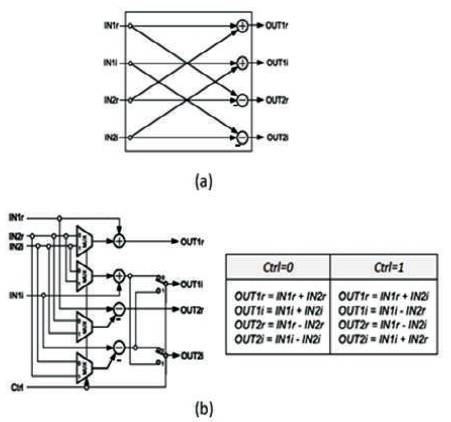
Figure 6. Butterfly Implementation (a) BFI, (b) BFII

This section presents the similar radix-2k FFT algorithms, Which are generated by using binary tree representation. Now based on the binar y tree presentation of Cooley- Tukey FFT algorithm, we generate the number of FFT algorithms which are identical to radix-2k. These algorithms can be generated by splitting N-point FFT into 2k-point and N - 2 Point. Apply this decomposition recursively until all sizes will become 2k. Then apply radix-2 decomposition on all 2k -Point FFTs as shown in Figure 7.

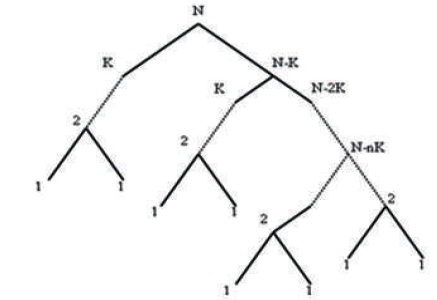
Figure 7. Signal Flow Graph of a Radix-2k FFT

Signal flow graph of a radix-2 FFT a signal flow graph (SFG) may be a one among the foremost popular graphical representations of FFT algorithms as shown in Figure 7. The flow graph consists of a series of stages, where each stage includes additions, subtractions and sophisticated multiplications. An example of 8-point FFT decomposition is shown in two steps. At first, it decomposes into 2-point and 4-point, this finishes up with a fourfold 2-point computation, twiddle factor multiplication, and twice 4-point in next stage. of these information is mapped on the binary tree and SFG are shown in Figure 8, where four different of butteries shows the fourfold 2- point FFT. At second stage, 4-point FFT is further decomposed in 2-point and 2-point.

The FFT algorithm for 16-Point radix-24 based FFT is shown in Figure 8.

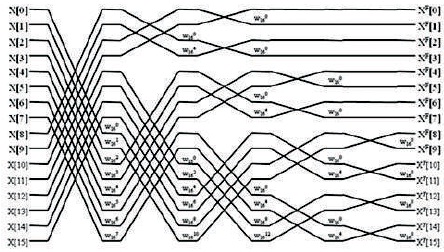
Figure 8. FFT Algorithm of 16-Point Radix-24 DIF FFT

The proposed a new 4 path delay feed forward FFT Architecture where we take input as four parts and those are feed to Butterfly architectures.

The proposed 4-Path FFT block diagram (Figure 9) shows the 16-Point 4-parallel radix-24 feed forward FFT architecture. The architecture is made up of a input storage which is used to process the input into 4 paths, radix-24 butterflies, and shuffling structures called commutators, which consist of buffers and multiplexers.

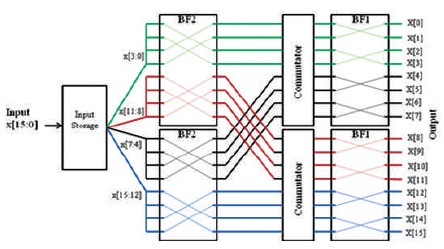
Figure 9. 16-Point 4-Paths Radix-24 FFT Processor

The proposed 4-Path FFT block diagram (Figure 10) shows the 128-Point 4-parallel radix-24 feed forward FFT architecture, which consist of 5 stages of butterfly units and commutators and an input storage which can partition the input samples into 4 parts and fed to 4 paths for FFT processing.

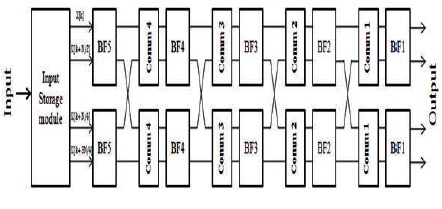
Figure 10. 4-Path Feed Forward FFT Architecture

3. Result and Discussion

In this paper present the radix-24 based 4-Path Delay Commutator FFT architecture for low power, high throughput applications. Combining benefits of radix- 22 , Radix-24 algorithm and feed forward architecture, the proposed 4-Path FFT processor achieves the lowest hardware requirements for multipliers and memory size in compared with delay feedback architecture and radix-K MDC and MDF.

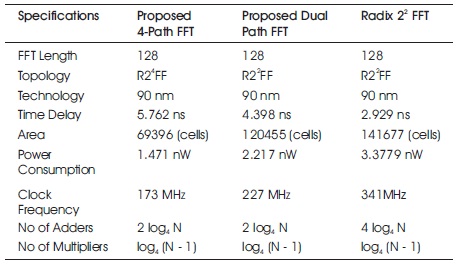
Table 1. Comparision Table between Proposed Work and Other FFT Designs

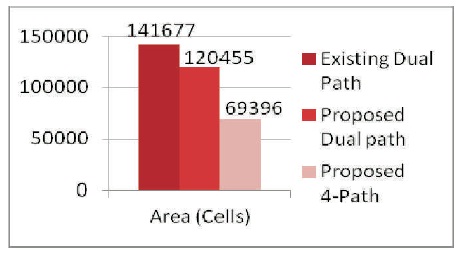
Figure 11. Area Comparisons Between Existing and Proposed FFTs

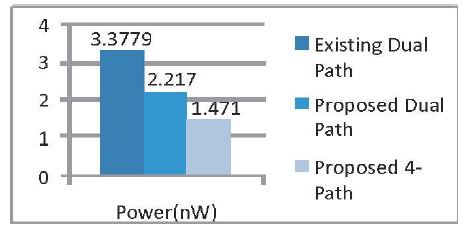
Figure 12. Power Comparison of Existing and Proposed FFTs

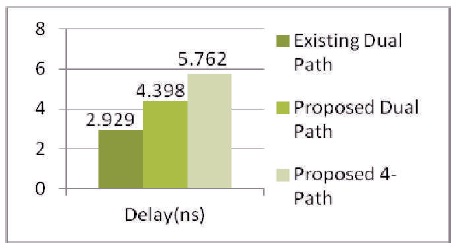
Figure 13. Delay Comparison of Existing and Proposed FFTs

Conclusion

This paper has presented a novel 4-Path Feed forward FFT processor whose outputs are generated in the natural order. The proposed processor can process the data into four independent data streams simultaneously, and thus by making it is suitable for many low power and area efficient real-time applications. Moreover, the proposed architecture provides higher performance than the prior architectures. These performance characteristics make the proposed 4-Path FFT processor superior in sense of hardware complexity and performance.

References

[1]. Birdsong, J. B., & Rummelt, N. I. (2016, September). The hexagonal fast Fourier transform. In 2016, IEEE International Conference on Image Processing (ICIP) (pp. 1809-1812). IEEE. https://doi.org/10.1109/ICIP.2016.7532670
[2]. Chen, Y., & Chen, H. (2013, April). A efficient design of a real-time FFT architecture based on FPGA. In IET International Radar Conference Proceedings. The Institution of Engineering & Technology. https://doi.org/10. 1049/cp.2013.0368
[3]. Chen, Y., Lin, Y. W., Tsao, Y. C., & Lee, C. Y. (2008), A 2.4- Gsample/s DVFS FFT processor for MIMO OFDM communication systems. IEEE Journal of Solid-State Circuits, 43(5), 1260-1273. https://doi.org/10.1109/JSSC. 2008.920320
[4]. Chen, Y., Yi-zhuang, X., Chen, L., Chen, H., & Deng, Y. (2015, October), Design of a configurable fixed-point FFT processor. IET International Radar Conference, The Institution of Engineering & Technology. https://doi.org/10. 1049/cp.2015.1307
[5]. Heideman, M., Johnson, D., & Burrus, C. (1984), Gauss and the history of the fast Fourier transform. IEEE ASSP Magazine, 1(4), 14-21. https://doi.org/10.1109/MASSP. 1984.1162257
[6]. Jeon, D., Seok, M., Chakrabarti, C., Blaauw, D., & Sylvester, D. (2011), A super-pipelined energy efficient subthreshold 240 MS/s FFT core in 65 nm CMOS. IEEE Journal of Solid-State Circuits, 47(1), 23-34. https://doi.org/ 10.1109/JSSC.2011.2169311
[7]. Jiang, L. X., Liu, C. Y., & Zhang, P. (2012, October), A novel overall in-place in-order prime factor FFT algorithm. In 2012 5th International Congress on Image and Signal Processing (pp. 1500-1503). IEEE. https://doi.org/ 10.1109/CISP.2012.6469906
[8]. Mangaiyarkarasi, V., & Paul, C. K. C. (2014, July), Performance analysis between radix2, radix4, mixed radix4-2 and mixed radix8-2 FFT. In Second International Conference on Current Trends In Engineering and Technology-ICCTET 2014 (pp. 430-434). IEEE. https: //doi.org/10.1109/ICCTET.2014.6966332
[9]. Mittal, S., Khan, Z. A., & Srinivas, M. B. (2007, November), Area efficient high speed architecture of Bruun's FFT for software defined radio. In IEEE GLOBECOM 2007-IEEE Global Telecommunications Conference (pp. 3118-3122). IEEE. https://doi.org/10.1109/GLOCOM.2007. 590
[10]. Mohapatra, B. N., & Mohapatra, R. K. (2017, February), FFT and sparse FFT techniques and applications. In 2017 Fourteenth International Conference on Wireless and Optical Communications Networks (WOCN) (pp. 1-5). IEEE. https://doi.org/10.1109/WOCN. 2017.8065859
[11]. Mookherjee, S., DeBrunner, L., & DeBrunner, V. (2015, November), A low power radix-2 FFT accelerator for FPGA. In 2015 49th Asilomar Conference on Signals, Systems and Computers (pp. 447-451). IEEE. https://doi.org/10.1109/ ACSSC.2015.7421167
[12]. Padma, C., Jagadamba, P., & Reddy, P. R. (2018), A review on optimized FFT architectures for wireless communication system, Journal of Advanced Research in Dynamical and Control Systems, 10(14s), 1654-1662.
[13]. Padma, C., Jagadamba, P., & Reddy, P. R. (2020), Implementation of high Performance FFT architecture for DSP applications, International Journal of Advanced Science and Technology, 29(3s), 582-593.
[14]. Salehi, S. A., Amirfattahi, R., & Parhi, K. K. (2013), Pipelined architectures for real-valued FFT and Hermitiansymmetric IFFT with real datapaths. IEEE Transactions on Circuits and Systems II: Express Briefs, 60(8), 507-511. https://doi.org/10.1109/TCSII.2013.2268411
[15]. Wang, A., & Chandrakasan, A. (2005), A 180-mV subthreshold FFT processor using a minimum energy design methodology. IEEE Journal of Solid-State Circuits, 40(1), 310-319. https://doi.org/10.1109/JSSC.2004.837945