Wireless communication system has grown tremendously with remarkable research effort and significant developments. Inter Symbol Interference (ISI) due to multipath, Cross Antenna Interference caused due to Multiple Antenna Transmission and Multi User Interference (MUI) occurred due to Multiple User Signal Synchronized Transmission are the major vulnerabilities of the wireless communication system. For future applications like 4-G or next generation broadband wireless communication, a system combined with multicarrier modulation which is very effective in combating severe multipath interference and providing multiple access simultaneously is mandatory. Recent development shows the advantage of combining Orthogonal Frequency-Division Multiplexing (OFDM) and Interleave Division Multiple-Access (IDMA) in an OFDM-IDMA scheme. OFDM suppresses the Inter-Symbol Interference (ISI) induced by multi-path channels, and the signals of different users (MUI) are avoided by user-specific interleavers based on the IDMA principle.

In OFDM-IDMA, IDMA (Interleave Division Multiple Access) is a novel technology that replaces the drawbacks of existing Code Division Multiple Access (CDMA) technique. In CDMA, interleaver is used for coding gain while in IDMA; they are engaged for user separation. The basic principle of IDMA is to use specific interleaver to differentiate the user. In order to immunize noise and Multiple Access Interference (MAI) at the receivers, selection of interleavers which are weakly correlated between different users is an important issue. The circumstance for IDMA to be successfully executed is that the interleaver between the transmitter and receiver should be identical. The desirable characteristics of IDMA interleaver codes include (i) availability of large number of codes (ii) impulsive auto-correlation function (iii)zero crosscorrelation values (iv) randomness (v) ease of generation (vi) Less hardware requirements (vii) High speed.

The stipulation for OFDM-IDMA to be successfully employed is that the transmitter and receiver concur upon the equivalent interleaver. Earlier OFDM-IDMA depended only on the random interleaver pattern .In the random interleavers, the entire interleaver matrix has to be transmitted to the receiver, which can be very costly. When the interleavers were generated randomly and selfregulating, the cross correlation between different interleavers is quite weak. The system requires more memory to hoard these interleaving patterns, because all of them will be used at the receiver for signal detection. Thus bandwidth must be reserved to modernize the interleaving information for OFDM-IDMA systems. When user number increases in the system, this issue becomes worse. Meanwhile, the interleaving procedure should be fast enough to achieve high speed data transmission for the OFDM-IDMA systems. In order to immunize noise and MAI for the receivers in OFDM-IDMA systems, it is necessary to choose good interleavers which are weakly correlated between different users. The aspiration is to construct a methodical interleaver pattern for IDMA such that it performs, as well as random interleavers satisfy the design criteria: The interleaver should be easy to stipulate and spawn, i.e., the transmitter and receiver requires a small size of bits to be in agreement upon an interleaver, and then generate it. The interleavers should not have a collision.

The random interleaver introduced by Li Ping [1] can randomize the MAI at the receiver end efficiently. But user side and Base Station (BS) have to store a large number of interleaving pattern information. Thus, the memory and bandwidth requirements are ridiculous for systems. The nested interleaver by Hao Wu [2] consists of a basic interleaver, with which a series of interleavers can be obtained with recursion method. Comparing with the random interleavers, the memory and bandwidth resources consumption will be greatly reduced. The orthogonal interleavers and the pseudo random interleavers were introduced by Popes [3]. The design of orthogonal interleavers was based on the PN (Pseudo noise) sequences. The pseudo random interleavers for different users depend on the primitive polynomials. Thus the specific user need to store their primitive polynomial. Obviously, this method is better than the nested and the random interleavers. When user number becomes large, it is difficult to find enough primitive polynomials for pseudo random interleavers, and systems have to endure generation time for nested interleavers. Thus, pseudo random interleavers and nested interleavers are not suitable for large scale OFDM-IDMA system. The circular shifting interleaver [4] does a good job of permuting weight-2 input sequences with low codeword weights into weight-2 input sequences with high codeword weights. However, because of the regularity inherent in this type of interleaver, it may be difficult to permute higher weight (weight>2) input sequences with low codeword weights into other input sequences with high codeword weights.

In this paper,the use of the deterministic interleaver is proposed. The receiver is designed to generate the interleaver based on the user index k. This paper, deals with the design and peak correlation analysis of a deterministic chip-level interleaver. Neither the entire random interleaver matrix, nor the power interleaver needs to be transmitted. The system model of OFDM-IDMA is explained in Section 1. It is followed by the design of deterministic interleaver in Section 2.The MAI analysis is mentioned in Section 3. Peak correlation and correlation analysis is discussed in Section 4, 5 and 6. Simulation analysis is reported in Section 7 followed by a conclusion.

OFDM-IDMA [5] inherits most of the merits of OFDM and IDMA system. The key advantage of OFDM-IDMA is that Multi User Detection (MUD) can be realized efficiently with complexity per user independent of the channel length and the number of users. The transmitter/receiver structure of an OFDM-IDMA system with K users is shown in Figure 1.

Figure 1. OFDM –IDMA System Model

This section briefs about the functioning of OFDM-IDMA transmitter and receiver. OFDM-IDMA consists of a base station and a number of users who transmit the data. Let the available bandwidth be divided among say k users. Thus the sub carriers are also k. The information bit from a single user is encoded by using low Forward Error Correcting Code [FEC] and a Spreader. A spreader is simply a repetition code and it consists of +1 and -1 alternatively e.g.{+1 ,-1,+1,-1,….}.Then the coded data is interleaved using a specific interleaver. The interleaved data is mapped to a sequence using a modulator. Here a BPSK modulator is preferred .The sequence is modulated onto sub carriers by using an N point IFFT.

The signal received at the base station is a superposition of all active users. The received signal is passed through OFDM demodulation network .The demodulation network comprises of FFT and removal of cyclic prefix. Then the signal is passed through iterative IDMA. Iterative IDMA comprises of Elementary Signal Estimator (ESE) and Decoders. The process that is executed in iterative IDMA is explained as follows, the signal from OFDM demodulator is passed through Elementary Signal Estimator. The ESE e_ESE (X_K(j)) process generates posterior Log Likelihood Ratios (LLRs) of the given signal (symbol).

(1)

(2)

Where, E (X_K (j)) is the mean and Var (X_K (j)) is the variance of the transmitted bits.

(3)

(4)

e_ESE(X_k(j)) is sent to the APP-DEC after de-interleaving. The e_dec generated by the APP-DEC is sent to the ESE through the interleaving and the process is iterated. Once the iteration is over the decoder produces hard decision to estimate the transmitted bits.

In this paper, two new deterministic interleaver namely Modified Circular Shifting Interleaver and Clockwise Interleaver are introduced. Deterministic Interleavers [6] are constructed using a mathematical expression. The receiver automaticaly generates the interleaver based on the user index k. It is generated easily and time taken for generation is feasible. This aims at reducing the bandwidth and the memory requirement of the systems which employ random interleavers.

This interleaver is acquired from Circular Shift Interleaver [4] which was defined by the equation

P(i)=(a(i)+s)mod L , Where a is a prime number, I is the index and s is the offset and a < L and s < 1.

Figure 2. The flow chart briefs the design procedure of (P * Q) mod N interleaver.

Figure 2 explains the flow chart for the design of (P * Q) Mod N Modified circular shift interleaver [6] is specified as

(5)

The deinterleaver is obtained by using the symmetry property of modulus arithmetic

(6)

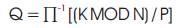
Π represents the interleaver and Π^-1 denotes the deinterleaver. Generally Π and Π^-1 are self inverse to each other. P denotes any prime number and N denotes the size of the coded data. Also Q and K denotes the bit position. Q resembles the existing bit position of the coded data and K denotes the new interleaver position. Normally the prime number P chosen should not be a factor of N. In that case interleaving pattern is not obtained. Depending upon the number of user to be allotted distinctive prime number is chosen for each user.

Step 1: The length of the interleaver sequence is N. Let the bit position q, of the interleaver be 0 to N-1.

Step 2: Allot a unique prime number to each user. A prime number chosen should not be a factor of N.

Step 3: The interleaved bit position is obtained using equation 1.

Step4: The deinterleaved pattern is obtained using equation 2.

Example

Consider N to be 8 bits such that {0, 1, 2, 3, 4, 5, 6, 7}. Let the prime number be 3 then the new location of bit will be as follows let

Another deterministic interleaver mentioned here is different from the above one in the type of seed used. Instead of prime number the user index itself is used as the seed. To calculate (X+k)mod L, the flow chart is given in Figure 3.

(7)

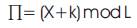
X indicates the user number and k indicates the bit position with L as the length of the interleaver.

(8)

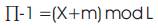
The de-interleaver is obtained by using the symmetry property of modulus arithmetic

Step 1: The length of the interleaver sequence is L.Let the bit position k, of the interleaver be 0 to L ^-1.

Step 2: The user index is assigned as seed. Assign the user number itself as X

Step 3: The interleaved bit position is obtained by equation (7).

Step 4: The de-interleaved bit position is obtained by equation (8).

The benefit of clockwise interleaver is that number of user allotted depends on the size of the interleaver.

Example

Consider the user number to be 3 and the consecutive bits position K be {0, 1, 2, 3, 4-------L-1}.Assume L to be 8 then the new location of the bit becomes,

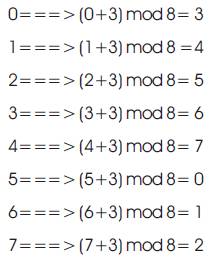
Now, the new order of bits will be {3,4,5,6,7,0,1,2}.

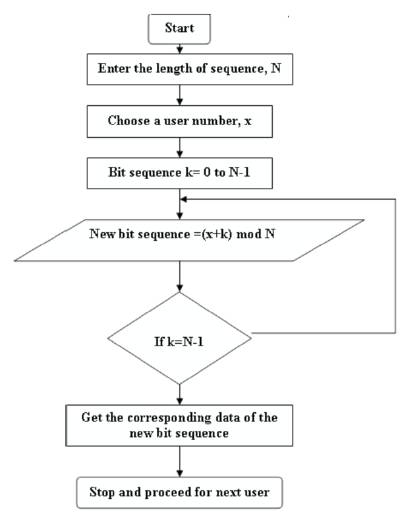
Figure 3. The flow chart briefs the design procedure of (x+k) mod L interleaver

Assume that there are only two users in the system and noiseless channel is used. The data of user1 is encoded by C and permuted by Π₁ .At the receiver end the received signal is C₁*Π₁ + C₂*Π₂ .The received signal is de-interleaved by Π1-1 .Now the input information of decoder is C₁ + C₂ *Π₂ *Π₁^-1 . If C₁ and C₂ *Π₂ *Π₁^-1 are orthogonal to each other, than the interference from user2 can be eliminated. To suppress the MAI (Multiple Access Interference) the cross correlation between them need to be zero.

(9)

So the orthogonal interleavers can be defined as following. For any two coded words, ci and cj, are permuted by two different interleavers Π 1 and Π2 respectively, if their cross correlation is zero

(10)

The orthogonal attribute of OFDM-IDMA systems which is illustrated in Figure 4 has bond with coded data pattern and interleaving scheme. Thus, it is complicated to achieve orthogonal interleavers in the practical OFDMIDMA systems. Generally, weakly correlated interleavers can be used in the OFDM-IDMA system to obtain good performance. Since correlation of different interleavers is affected by the coded data pattern, we use Peak Correlation [3] to analyze the correlation issues for simplification in this paper.

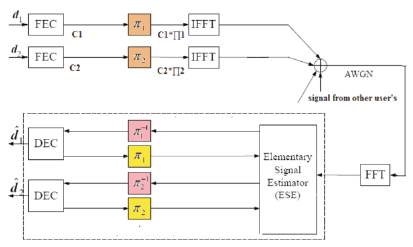
Figure 4. OFDM-IDMA with two users

Auto-correlation is a measure of the similarity between a code C (t) and its time shifted replica [7]. Mathematically defined as

(11)

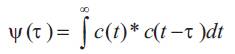
Ideally, this Auto-Correlation Function (ACF) should be spontaneous i.e. peak value at zero time shift and zero values at all other time-shifts (i.e. side-lobes). This is required at the receiver side for proper harmonization and to discriminate the desired user from other users producing MAI.

Cross-correlation [7] is the measure of similarity between two different code sequences C1 (t) and C2 (t). Mathematically, it is defined as:

(12)

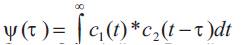
Cross-Correlation Function (CCF) designates the correlation between the desired and undesired code sequences at the receiver. Therefore, in order to eliminate the effect of multiple access interference at the receiver, the cross-correlation value is obliged to zero at all time shifts.

The Peak Correlation numerical results of modified circular shifting interleavers and clockwise interleaver are calculated. For comparison, the Peak Correlation performances of orthogonal interleaver, modified circular shift interleaver and clockwise interleaver are also studied. Generally for an orthogonal interleaver the auto correlation is highest and cross correlation is zero. The Peak Correlation numerical results are calculated for a sample of interleaver size 16 for five users. The prime numbers allotted for each user is 3, 5, 7,11and13 respectively. The data's observed are given in Tables 1, 2 and 3.

Table 1. Peak correlation of an ideal orthogonal Interleaver

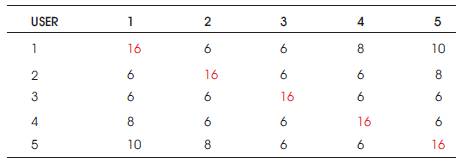
Table 2 . peak correlation of modified circular interleaver

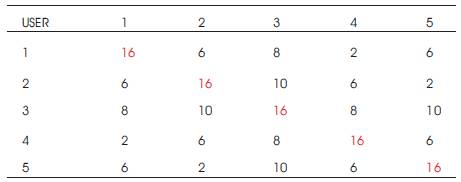
Table 3. peak correlation of clockwise interleaver

The diagonal elements in the above tables are autocorrelations and the other elements are the cross correlation between different users. From these tables above, we can see that the correlation values of modified shifting and clockwise interleavers are similar. The auto correlation has peak value at zero shifts. The maximum weight of the data is 10(1111010000111110).The peak cross correlation value lies between 1 and 10. When the length of the data is increased the cross correlation reduces close to zero.

When two interleaver sequences are strongly related then the correlation between them is '1'.When two interleavers are orthogonal to each other, then the correlation between them is “0”.The correlation of any two sequences lies between -1 to +1. If the correlation value approaches “0”then these sequences does not match each other. For orthogonality condition the value should be zero. The correlation for different user specific interleaver [6] may be defined. Let data1 and data2 be the two data sequences of two different user, say user1 and user2.Then find XOR of user 1 and user 2 as data1 XOR data2. Now calculate the amount of 1‟s after XORing the both user data as X and the amount of 0‟s after XORing the both user data as Y. Now correlation is given as

(13)

For clockwise interleaver, thirty users were considered with a data length of eight. The correlation is as follows

User specific cross correlation is 0.27.The above values are simulated and plotted in Figure 5 using Matlab.

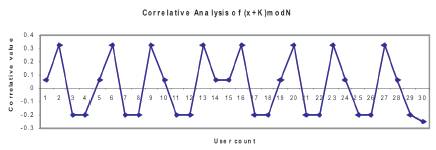
Figure 5. Correlation Analysis of (x+k) mod N interleaver with thirty user

For circular shifting interleaver thirty users were considered with a data length of eight .The correlation is as follows

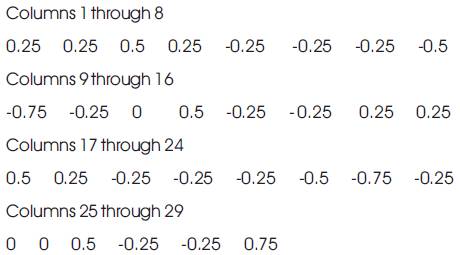
User specific cross correlation is -0.5 .The above values are simulated and plotted in Figure 6 using Matlab.

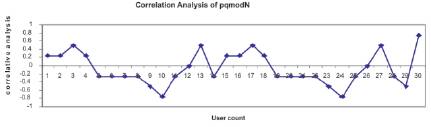
Figure 6. Correlation Analyses of (p*q) mod N for thirty user's

The comparison between modified circular shifting interleaver and clockwise interleaver is shown in Figure 7. We can examine that clockwise interleaver has perfect correlation between the interleavers than the modified circular shifting interleaver.

Figure 7. The chart enhances the comparison between the performance of both proposed interleaver with thirty user's.

The correlation value of random interleaver increases with the no. of users' .The deterministic interleaver indicates a correlation value less than one. The clockwise interleaver has a user specific cross correlation 0.27 which is nearly zero. This indicates that the collision between two interleavers is nearly zero. In the circular shifting interleaver the user specific cross correlation value is -0.5.The correlation value between -1 to 0 is acceptable. In future more deterministic interleavers are to be recognized and their performance should be studied.