The use of laminated structures namely plates and shells are inevitable for many engineering structures in the recent past. Laminates are used in ships, aircrafts, missiles, automobiles, mining equipments, railway wagon, and civil structures. The advantages of light weight, high strength, stability, corrosion resistance, ease of fabrication (Behera et al., 2018) and desired mechanical properties have increased the application of laminates at an affordable cost. The laminates are glued to the surface of concrete using an adhesive due to which the fibres in the laminates can carry the load and increase the load carrying capacity of the entire structure. The use of cutouts in laminates allows the engineer to inspect the structure, provide electrical ducts, allow access ports for mechanical systems, providing openings for doors and windows and so on (Brethee, 2009). The practicalities of using laminates require cutouts to be provided. The response of the laminates subjected to mechanical and thermal load changes when a cutout is provided in the continuum. Laminates are used at the bottom plate for some passage of liquid in liquid retaining structures (Bhardwaj et al., 2015). Laminates are glued to the soffit of the bridge decks (Harik & Peiris, 2017). It is well known that these laminates are exposed to undesirable changes in moisture content which may change the response considerably. Hence there is a need to study the behavior of laminated composite structures with cutouts precisely (Natarajan et al., 2014).

Composites are subjected to different environmental conditions during the service life. Change in moisture content and temperature have an adverse effect on the performance of composites. Strength and stiffness are reduced with the increase in moisture concentration and temperature. The deformation and stress analysis of laminated composite plates subjected to moisture has been the subject of research interest in recent years. The effect of changes in moisture content on the flexural behavior of laminated composite structures may lead to a failure, detach from the concrete surface and as a result unable to increase the load carrying capacity of the structure. The change in moisture content alone has more effect on laminates than change in temperature alone. This study is intensely focused on the effects of change in moisture content alone. The main focus of this study is to conduct hygroscopic analysis and measure the response of the structure in terms of bending moments, strain energy and deflection. The finite element analysis is performed using six node linear strain triangular elements.

The code written in Fortran is given wherever required and explained throughout the analysis. The deformed configuration of the shell and the Strain Energy distribution are presented.

To determine the deflections for laminated plates subjected to hygroscopic loading using six node linear strain triangular elements.

• The study is limited to linear static analysis only.
• The buckling of shells is not considered in this study.
• The material is free from any imperfections.
• The temperature remains constant.

Sriram and Sinha (1991) performed the finite element analysis using eight noded quadrilateral isoparametric plate bending element to study the effect of moisture and temperature on the bending behavior of laminated composite plates. The conventional finite element formulation includes hygrothermal strains and transverse shear deformation in the analysis. The results are presented for anti-symmetric cross ply and angle ply laminates consisting of graphite/epoxy laminate subjected to uniform distribution of moisture and temperature. No external mechanical loading is applied. In case of anti-symmetric cross ply laminates with simply supported boundary conditions subjected to uniform moisture concentrations, deflections are determined. They found that the deflection is maximum near the centre of the edge. The deflections along the diagonals is zero in case of SSSS plate. The FEM results are compared with the closed form solutions and found to be in close agreement. In case of clamped boundary conditions the maximum deflection is found to be less than the maximum deflection for a SSSS plate with similar loading. In case of symmetric cross ply laminated plates, the deflections were found to be zero. The moment resultant Mxy is a function of fibre orientation and increases with increase in the change in moisture content and temperature.

Chaubey et al. (2019) did their study on hygrothermal analysis of skew conoids. In case of skew shells, the edges of the boundary elements are not parallel to the global axis. It is not possible to specify the boundary conditions in terms of global displacements. Hence, it is necessary to use the edge displacements in the local coordinates. In their research work, they have used a nine noded curved isoparametric element with seven degrees of freedom at each node. Coding is done in Fortran and nondimensional central deflections and stresses were determined. A three layer SSSS square laminate under sinusoidal loading of amplitude q is analyzed and compared with 3D elastic solution. They found that the deflection decreases with increase in the aspect ratio. In case of skew conoids, the value of non-dimensional deflection of moderately thick shell under hygrothermal loading decreases with an increase in skew angle. The maximum dimensionless deflection increases for the 30 and 45 degrees skew angles and decreases for 15 and 60 degrees skew angles. It is observed that maximum deflection depends upon hl/hh ratio and skew angle and also boundary conditions as well. Bending of symmetric cross-ply multi-layered plates in HT environments is studied by Zenkour and Alghanmi (2016). Symmetric cross-ply laminated plates in hygrothermal environment are analyzed using sinusoidal shear deformation plate theory (SSPT). The results obtained using higher order shear deformation theory (HPT) are in close agreement with those obtained with SSPT for thicker plates. The dimensionless central deflections increase upto aspect ratio 1.5 and decrease with aspect ratio equal to 2. The effect of transverse shear deformation must always be incorporated into the analysis because classical plate theory (CPT) under predicts the deflection and transverse shear stress and over predicts the normal stresses. The deflections calculated due to HPT, SSPT and FPT decrease with increase in the side to thickness ratio. The deflection obtained by applying all plate theories increase as the ratio of E1/E2 increases. The authors have concluded that SSPT gives accurate results than other theories. Hygrothermal effects on the flexural strength of laminated composite cylindrical panels were explained by Mahapatra and Panda (2016). They developed a nonlinear finite element computer code in MATLAB. The present model is developed based on higher order shear deformation theory and Green Lagrange nonlinearity and includes the higher order nonlinear terms in the formulation which makes the model more realistic in nature. Linear and nonlinear flexural responses of simply supported laminated composite spherical panel is analyzed and compared. They found that a mesh size of 6x6 is enough to obtain a converged results. The graph between mesh density versus nondimensional central deflection shows that deflections obtained were high with a mesh size of 3x3 and decreased linearly with increase in mesh density upto 6x6. The results have shown that for cylindrical shells with symmetric lamination are less affected under hygrothermal loads in comparison to antisymmetric laminations. For the simply supported square thin (a/h=100) anti-symmetric cross ply laminated composite cylindrical panels, the non-linear deflections increase as the curvature ratio increases irrespective of the hygrothermal loading conditions. This is because of the fact that as the curvature ratio increases the panel becomes flat and the membrane stiffness decreases substantially. Effect of HT environment on the nonlinear free vibration responses of laminated composite plates is researched. The author Mahapatra et al. (2016) have developed MATLAB code to conduct the investigation. They found that for 100 degrees change in temperature and 1% change in moisture content, side-to-thickness ratio 20, aspect ratio equal to one, the frequency values are high at lower amplitude ratios. The values are then compared with the values given, which showed similar results. They observed that nonlinear frequency parameter increases with thickness ratio and decrease with hygrothermal loading. However nonlinearity is more pronounced at higher amplitude ratio. The nonlinear frequency parameter of, anti-symmetric angle ply (+/- 60) laminated square plates (a/h=70) for four different support conditions. It is observed that the non-dimensional frequency parameters are least for simply supported and higher for clamped boundary conditions. Nonlinear vibration responses of symmetric laminated plates are higher in comparison to the antisymmetric laminations. It is observed that for equal number of layers and particular hygrothermal load, cross ply laminates exhibit higher non-linear frequencies than the angle ply laminates. Hygrothermal effects on free vibration and buckling of laminated composite with cutouts is studied by Natarajan et al. (2014). In his paper, the effect of moisture concentration and thermal gradient on the free flexural vibration and buckling of laminated composite plates is investigated. The effect of a centrally located cutout on the global response is studied in this paper. Square plates and rectangular plates with simply supported and clamped conditions with two different cutout shapes that are circular and elliptical are considered in this study. The critical load and the natural frequency of a cross ply laminate exposed to moisture and temperature are compared with the Ritz solutions. They found that for the moisture concentration of 1% and 325 K temperature, the frequencies decrease with increase in mesh size and critical load decreases with increase in mesh sizes. The authors have taken a mesh size of 30x30. They observed that with the increase in temperature the fundamental frequency decreases, and with increase in cutout radius the fundamental frequency increases. With the increase in orientation from 0 to 90, the frequency decreases and reaches minimum when the cutout orientation is 60 and with further increase in orientation the frequency increases. Increase in moisture concentration and side to thickness ratio, the critical load increases. Increase in cutout radius, moisture concentration and thermal gradient, the critical buckling load decreases and this can be attributed to the stiffness degradation.

Boukert did his work on HT mechanical behavior of thick composite plates using High order theory (Boukert et al., 2017). Higher order theory developed by Reddy has been used to evaluate the influence of hygrothermo mechanical behavior of thick composite plate. Simulations have been made for a cross ply thick plate with different loads. The plate composed of four crossed layers 0/90/90/0 is subjected to purely mechanical, thermomechanical, hygrothermomechanical loading with zero boundary condition for temperature and humidity in the upper and lower face of the plate. The plate is under a transverse sinusoidal mechanical loading type coupled with different types of thermal and hygroscopic loading. The results show a contradictory role in the behavior of thick composite plates. An important and direct influence of the hygrothermal loading has been observed on the longitudinal, transversal, longitudinal tangential stresses, a very weak influence has been observed for the transverse shear stress. Vibration behavior of laminated composite flat panel under hygrothermal environment is presented. Kar et al. (2015) have studied the influence of mesh size on the non-dimensional fundamental frequency. The linear frequencies are obtained at 0 and 50 degrees temperature. Based on the convergence a 5 x 5 mesh is found adequate for analysis. They found that nondimensional fundamental frequencies of present model gives lower non-linear frequency values than the reference values for room temperature whereas the frequency increases as the temperature load increases. The nondimensional fundamental frequencies are increasing along with the increase in amplitude ratio at 0 and 50 degrees temperature. Higher rate of increase in observed for thinner plates than thicker plates. The effect of variation of moisture concentration is slightly superior at lower temperatures. For equal number of layers, anti symmetric cross ply laminates exhibit higher nonlinear frequencies than the hybrid laminates. However at very high temperatures and moisture concentration both behave equally. Some authors did their study on an isotropric homogeneous square plate having side-to-thickness ratio 100 and subjected to a linear temperature across the thickness and uniform over the surface. The semi loof shell element consists of three types of nodes that are conventional corner and midside nodes, loof nodes at gauss points on the sides, central node. Two types symmetric laminates are subjected to linear thermal gradient across the thickness and uniform across the surface. The range is taken as -100 F to 400 F. From the results, they noticed that the stress at the bottom layer is higher than that of the top layer, even though the temperature is low at the bottom. The normal displacement reduces to half when the aspect ratio is increased from 1 to 2. For a square laminate, the resultant moment is positive and becomes negative as the aspect ratio increases.

In this section the outlines of the formulation required to perform the analysis for LEPS is described.

The constitutive Equations for the shell are given by,

(1)

Where N_x, N_y, N_xy are the in-plane force resultants, M_x, M_y,and M_xy are the moment resultants, Q_x, Q_y, are the transverse shear resultants.

The force and moment resultants are expressed as,

(2)

The elements of stiffness matrix [D],

(3)

where Q_ij are the elements of elastic constant matrix

(4)

(5)

where,

(6)

F_i and F_j are the two factors which is considered as one when the shell is thin. When the shell is moderately thick the product is considered as 5/6 as this is the shear correction factor from the theory of elasticity. Figure 1 shows the layers of lamina.

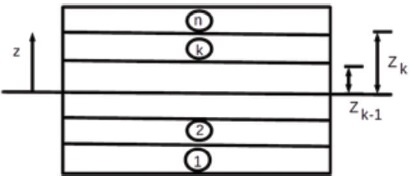
Figure 1. Layers of Lamina

The strain displacement relations of first order theory of shells,

(7)

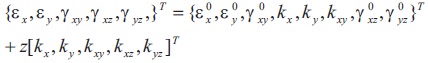
where,

(8)

4.1 Finite Element Formulation for Shell

A six node curved quadratic orthotropic triangular finite element is used for shell analysis. Five degrees of freedom are defined at every node (u, v, w,α, β). The relations between the displacement with respect to ξ and η coordinates and degrees of freedom.

(9)

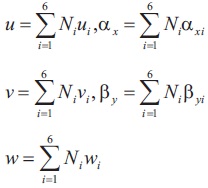
4.1.1 Shape Functions for the Six Node Triangular Element

(10)

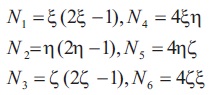
Figure 2 explains how the node numbers are identified for each element. The encircled numbers show the element numbers. The numbers adjacent to the dots are the node numbers. For each element the node numbers are calculated in clockwise direction.

Figure 2. 2x2 with 6 Noded Triangular Element

The displacements of the elements can be expressed in terms of shape functions and nodal degrees of freedom.

(11)

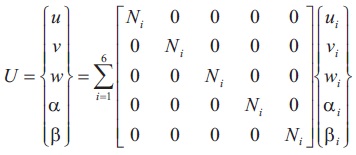
Stiffness matrix of the element will be solved by numerical integration method.

4.1.2 Stiffness Matrix for an Element

{ε}=[B]{δ}

(12)

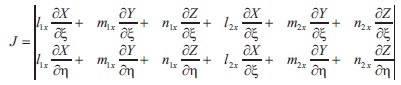
Stiffness matrix of the element will be solved by numerical integration method.

4.1.3 Hygro Thermal analysis (Université Libre de Bruxelles, n.d.)

Strain Tensor

 

(13)

(14)

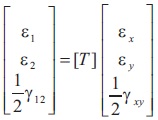
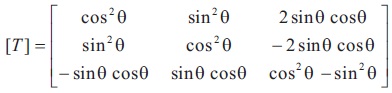
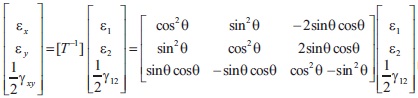
Thermal shear

(15)

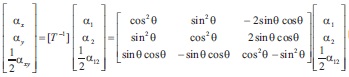
Similarly,

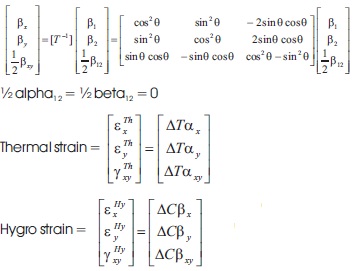
Total strain = Mechanical strain + thermal Strain + Hygro strain

(16)

The mechanical strain is given by,

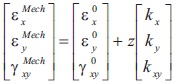
The total strain is given as,

(17)

The stress is given as,

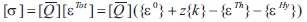
where (Shojaee et al., 2012),

(18)

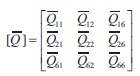
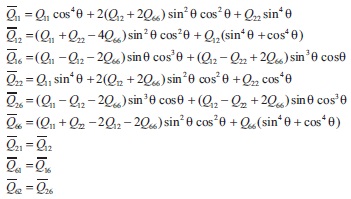
with,

(19)

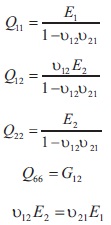
In the presence of external forces,

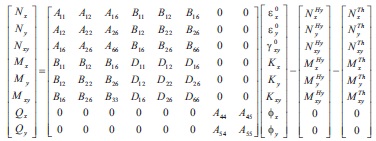
In the absence of external forces (Thai et al., 2013),

(20)

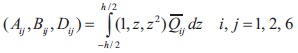
The element level stiffness matrix is given by (Ram & Sinha, 1991),

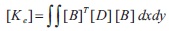
The element level nodal load vector due to mechanical forces is given as,

The element level nodal load vector due to hygrothermal forces is given as,

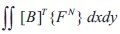
The solution for the nodal displacements is obtained from the equilibrium condition.

(21)

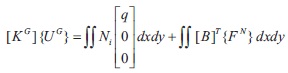
where K^G is global stiffness matrix and U^G is the global nodal displacement vector.

5. Problem Statement

To study the bending characteristics namely Displacement, Bending Moment, and Strain Energy for the following different problems.

• To perform a step by step analysis of SSSS plate having 0/90/0/90 lamina subjected to 1% change in moisture content.
• To analyze SSSS plate having 0/90/0/90 lamina for different aspect ratio subjected to different moisture content 0.25%, 0.5%, 0.75%, 1.0%, 1.25%, 1.5%.

6. Terms Used

6.1 Notations

The support notations are as shown in the Figure 3. The clamped support is shown in Figure 3a, in which the rotations and displacement is not allowed. The simply supported support is as shown in Figure 3b, where the rotations at the support are allowed.

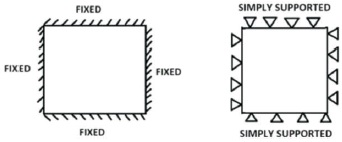
Figure 3. Support Notations (a) Clamped (b) Simply Supported

6.2 Geometry

The size of the plate is 100 mm x 100 mm.

7. A step-by-step Analysis of SSSS Plate having 0/90/0/90 Lamina with 1.0% Change in Moisture Content

7.1 Input Data

The dimensions of the plate is 100 mm x 100 mm.

The thickness of the plate is 1 mm.

The Young's modulus of elasticity in direction 1 is

E₁₁ = E_xx = 130000 MPa.

The Young's modulus of elasticity in direction 2 is

E₂₂ = E_yy = 8500 MPa.

The shear modulus of elasticity in direction 12 is

G₁₂ = G_xy = 6000 MPa.

The shear modulus of elasticity in direction 13 is

G₁₃ = G_xz = 6000 MPa.

The shear modulus of elasticity in direction 23 is

G₂₃ = G_yz = 3000 Mpa.

The elastic moduli of graphite/epoxy is given in Table 1.

Table 1. Elastic Moduli of Graphite/Epoxy Lamina at Different Moisture Concentrations G₁₃ = G₁₂, G₂₃ =0.5 G₁₂, ᶹ₁₂ =0.3, β₁=0, β₂=0.44

The Poisson's ratio ᶹ₁₂ is equal to 0.3.

The number of divisions along x-axis (1 direction) is equal to 10.

The number of divisions along y-axis (2 direction) is equal to 10.

The mesh is made of 6 node linear strain triangular elements.

The number of Gauss points is equal to three.

The number of degrees of freedom per node is equal to five namely u, v, w, θ_x, θ_y.

The displacement conditions for nodes along x-axis at the boundary is 10110.

The displacement conditions for nodes along the y-axis at the boundary is 01101.

The displacement conditions for nodes at the four corners are 11111.

The value of β₁ = 0 and β₂= 0.44.

The change in moisture content is equal to

∆c = 1.0% = 0.01.

The total number of joints is equal to 441.

The total number of elements is equal to 400.

The size of the stiffness matrix is equal to the number of joints multiplied by degrees of freedom per node is

441*5 = 2205.

7.2 SSSS Plate having 0/90/0/90 Lamina

Step by step procedure to perform the hygroscopic analysis of laminated composite plate.

The six node triangular element is as shown in Figure 4.

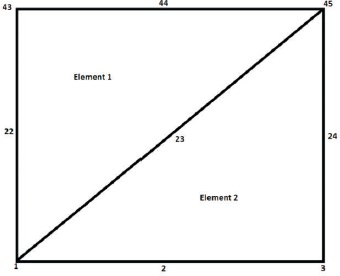
Figure 4. Six Node Triangular Elements

The element node connectivity is given in Table 2 and the coordinates of the nodes are given in the Table 3.

Table 2. Showing the Element Node Connectivity Table

Table 3. The X, Y Node Coordinates

7.2.1 Shape Functions

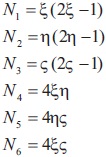
and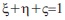

Derivatives of the shape functions:

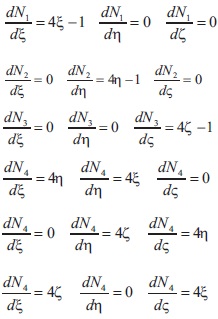
Jacobian of the element 1 is given at each Gauss point. Gauss points and their corresponding weights is given in Table 5.

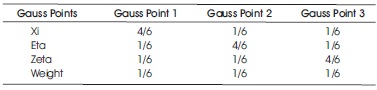
Table 4. Gauss Points and their Corresponding Weights

Element 1 Gauss point 1

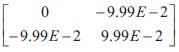
Element 1 Gauss point 2

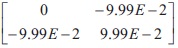
Element 1 Gauss point 3

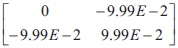
Element 2 Gauss point 1

Element 2 Gauss point 2

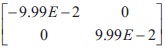
Element 2 Gauss point 3

7.2.2 Elasticity Matrix

Poisson ratio in the 2^nd direction is Nu21 = Nu12 * E22/E11 = 1.96153846153846144E-002

The program segment used for calculating elasticity matrix developed using Fortran is listed.

Let,

AM = 1/(1-NU12*NU21) = 1.0059194490656556

QXX = E11*AM = 130769.52837853522

QYY = E22*AM = 8550.3153170580717

QXY = QXX * PRY = 2565.0945951174217

Let Z(1) = -(thickness)/2.0 = -0.50000000000000000

Z(2) = -0.25000000000000000

Z(3) = 0.0000000000000000

Z(4) = 0.25000000000000000

Z(5) = 0.50000000000000000

Laminae = 0/90/0/90

For theta = 0, K = 1

Let C1 = cos(theta)

S1 = sin(theta)

U1 = cos⁴(theta)

U2 = sin⁴(theta)

U3 = cos²(theta)*sin²(theta)

U4 = (C1*C1-S1*S1)*(C1*C1-S1*S1)

U5 = C1 * S1 * S1 * S1

U6 = C1 * C1* C1 * S1

Q(1,1)=U1*QXX+U2*QYY+2.*U3*(QXY+2.*GXY)

Q(1,2)=U3*(QXX+QYY-4.*GXY)+(U1+U2)*QXY

Q(1,3)=U6*QXX-U5*QYY+(U5-U6)*(QXY+2.*GXY)

Q(2,1)=Q(1,2)

Q(2,2)=U2*QXX+U1*QYY+2.*U3*(QXY+2.*GXY)

Q(2,3)=U5*QXX-U6*QYY+(U6-U5)*(QXY+2.*GXY)

Q(3,1)=Q(1,3)

Q(3,2)=Q(2,3)

Q(3,3)=U3*(QXX+QYY-2.*QXY)+U4*GXY

Q(4,4)=C1*C1*GXZ+S1*S1*GYZ

Q(4,5)=C1*S1*(GXZ-GYZ)

Q(5,4)=Q(4,5)

Q(5,5)=C1*C1*GYZ+S1*S1*GXZ

For I = 1 To 5

For J = 1 To 5

A(I,J)=A(I,J) + Q(I,J)*(Z(K+1)-Z(K))

B(I,J) = B(I,J) + Q(I,J) * (Z(K+1)**2-Z(K)**2)*0.5

D(I,J) = D(I,J) + Q(I,J) * (Z(K+1)**3-Z(K)**3)/3.0

Continue J

Continue I

The output of the calculated elasticity matrix is shown in Table 5.

Table 5. Elasticity Matrix for SSSS Plate having 0/90/0/90 Lamina

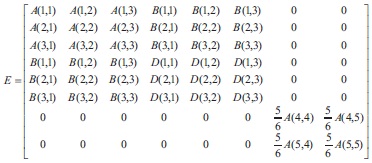
Hygroscopic loading has been analyzed using six node linear strain triangle, and the value at each node are calculated.

FH,1 = 24.45389

FH,2 = 24.45390

FH,3 = 8.324E-003

FH,4 = 1.64593

FH,5 = -1.64593

FH,6 = 1.040577E-003

Tables 6 hygroscopic load vector multiplied by strain displacement matrix respectively and subjected to change in moisture content of 1%.

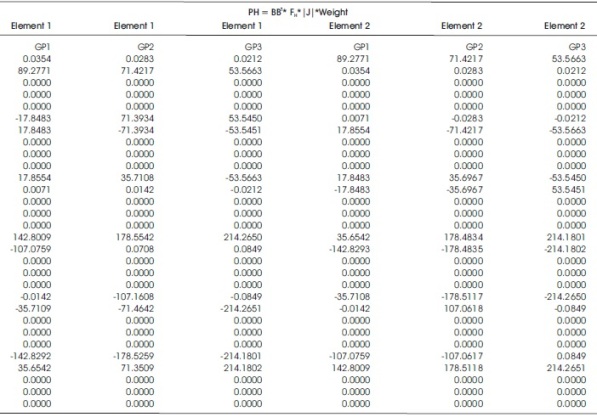
Table 6. Hygroscopic Load Vector Multiply with Strain Displacement Matrix

Assemble the global stiffness matrix and force vector and solve the simultaneous equations using Gauss elimination method. The maximum nodal z-displacement is equal to 0.0614321 mm at Node 214. The deformed shape due to change in moisture content of 1% is as shown in the Figure 5. The vertical deflections along the diagonal is nearly equal to zero.

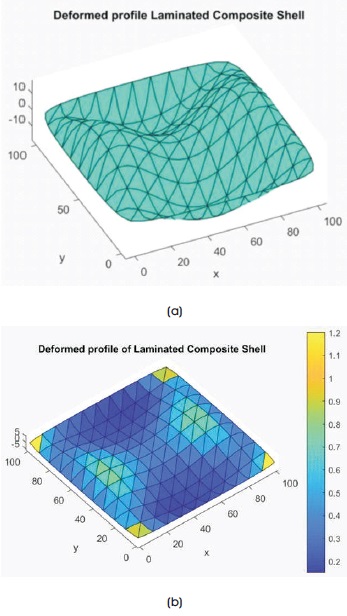
Figure 5. The Deformed Shape (Magnified) of the SSSS Laminated Composite Plate Having 0/90/0/90 Lamina Using Six Node Triangular Elements with Change in Moisture Content of 1% (a) Deformed Shape of the Plate (b) Distribution of Strain Energ

Step wise procedure to calculate the nodal stresses are,

• The stresses in each element are calculated at the centroid of each element.
• The stresses are assumed to be constant throughout the element.
• All the six nodes of each element have same stress field.
• At each node, the stresses for each element having a node in common are averaged.
• The final nodal stress values are obtained by taking the nodal stress calculated above minus the hygroscopic force vector.

The nodal stress calculated using the centroidal stresses at each element are lower than the stresses calculated at the corners using the extrapolation method discussed in the literature. The moments Mx, My at the centre of the plate are equal and opposite. The Bending moment M_x, M_y, M_xy at the centre node 221 are found to be M_x = -7.3635 Mpa, M_y = 7.3635 MPa, M_xy = -0.00156 MPa. The moment M_x and M_y at the centre node 221 of the plate are equal in magnitude and opposite in sign. The moment resultant M_xy at the centre node 221 of the plate is equal to zero.

The vertical deflections along the centre line as shown in Figure 6 are plotted. Figure 7 shows the deflection curves of SSSS plate having 0/90/0/90 lamina along the centre line at different moisture contents. The maximum displacement occurs at the centre of the edge at an inner node N214 and N228. The moisture content is varied from 0.25% to 1.5% in steps of 0.25%. The deflection curves are parallel and non-intersecting for all moisture contents. The maximum deflection is observed when the moisture content is 1.5%

Figure 6. The Centre Line of Plate Along the Displacements Plotted

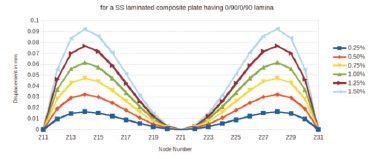
Figure 7. Graph Showing the Variation of Displacement on Y-axis and Node Number on X-axis for 100 mm x 100 mm, a/t =100 SSSS Laminated Composite Plate having 0/90/0/90 Lamina for Different Values of Moisture Content

Table 7 shows the vertical deflection at the nodes along the centre line of the SSSS laminated composite plate having 0/90/0/90 lamina at different values of moisture content. Table 8 shows the maximum deflection for different aspect ratios and moisture content varying from 0.25% to 1.5%.

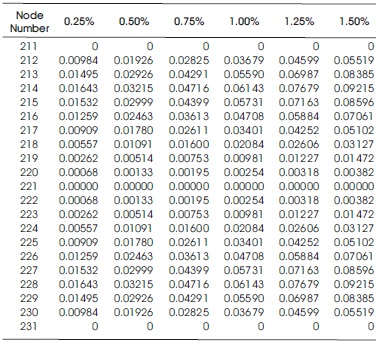
Table 7. Vertical Deflection in mm for Nodes along the Centre of the SSSS Composite Laminate Plate having 0/90/0/90 Lamina for Different Values of Moisture Content

Table 8. Maximum Vertical Displacement in mm at Node 214 for SSSS Laminated Composite Plate for Different Moisture Content and Side to Thickness Ratio (a/t) with 0/90/0/90 Lamina

The maximum displacement at the node increases with the increase in the aspect ratio and moisture content. The vertical displacement is higher for the SSSS plate when aspect ratio is 200 over the displacement calculated when the aspect ratio is 50. Similar pattern is observed at all moisture contents as shown in Figure 8, the lines are parallel and non-intersecting.

Conclusion

In this study, the Hygroscopic analysis of laminated composite plates and shells having different lamina nd with different boundary conditions is presented. The results of nodal displacements, and stresses along a section chosen are presented. A three dimensional image can solve this requirement to understand the behavior of the structure at each and every node. The interpretation of the results can be better and precise.

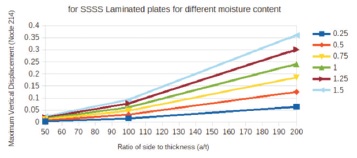
Figure 8. Variation of Maximum Displacement on y-axis and Side to Thickness Ratio on x-axis for SSSS Plate having 0/90/0/90 Lamina

The simply supported plate with lamina (0/90/0/90) subjected to hygroscopic loading has been analyzed using six node linear strain triangle. The results of the deformed shape of the structure show that the displacement is maximum near the centre of the edge. The displacement is zero at the centre of the plate and the displacement along the diagonals is also found to be zero. At the centre of the plate the moments are equal in magnitude and opposite in direction. The Strain Energy is maximum near the centre of the edges of the plate shown using the color band.

Future Study

The current study can be further carried as follows:

• Non-linear analysis can be performed to determine the bending characteristics.
• Vibrational analysis can be performed to determine the natural frequencies and mode shapes.

References

[1]. Behera, R. K., Garg, K., Patro, S. S., & Sharma, N. (2018, July). Eigen-frequency analysis of spherical shell laminated composite plates with and without central cutouts using finite elements. In IOP Conference Series: Materials Science and Engineering (Vol. 390, No. 1). IOP Publishing. https://doi.org/10.1088/1757-899X/390/1/012043

[2]. Bhardwaj, H., Vimal, J., & Sharma, A. (2015). Study of free vibration analysis of laminated composite plates with triangular cutouts. Engineering Solid Mechanics, 3(1), 43-50.

[3]. Boukert, B., Benkhedda, A., Bedia, E. A., & Khodjet- Kesba, M. (2017). Hygrothermomechanical behavior of thick composite plates using high order theory. Procedia Structural Integrity, 5, 115-122. https://doi.org/10.1016/j. prostr.2017.07.076

[4]. Brethee, K. F. (2009). Free vibration analysis of a symmetric and anti-symmetric laminated composite plates with a cutout at the center. Al-Qadisiyah Journal for Engineering Sciences, 2(2), 324-334.

[5]. Chaubey, A., Kumar, A., Fic, S., Barnat-Hunek, D., & Sadowska-Buraczewska, B. (2019). Hygrothermal analysis of laminated composite skew conoids. Materials, 12(2), 225-241. https://doi.org/10.3390/ma12020225

[6]. Harik, I., & Peiris, A. (2017). 20 years of CFRP Kentucky's bridges. In Proceedings of Fourth Conference on Smart monitoring, Assessment and Rehabilitation of Structures.

[7]. Kar, V. R., Mahapatra, T. R., & Panda, S. K. (2015). Nonlinear flexural analysis of laminated composite flat panel under hygro-thermo-mechanical loading. Steel and Composite Structures, 19(4), 1011-1033. https://doi.org/ 10.12989/scs.2015.19.4.1011

[8]. Mahapatra, T. R., & Panda, S. K. (2016, February). Hygrothermal effects on the flexural strength of laminated composite cylindrical panels. In IOP Conference Series: Materials Science and Engineering (Vol. 115, No. 1). IOP Publishing. https://doi.org/10.1088/1757-899X/115/1/012040

[9]. Mahapatra, T. R., Panda, S. K., & Dash, S. (2016, September). Effect of hygrothermal environment on the nonlinear free vibration responses of laminated composite plates: A nonlinear Unite element micromechanical approach. In IOP Conference Series: Materials Science and Engineering (Vol. 149, No. 1). IOP Publishing. https://doi. org/10.1088/1757-899X/149/1/012151

[10]. Natarajan, S., Deogekar, P. S., Manickam, G., & Belouettar, S. (2014). Hygrothermal effects on the free vibration and buckling of laminated composites with cutouts. Composite Structures, 108, 848-855. https://doi. org/10.1016/j.compstruct.2013.10.009

[11]. Ram, K. S., & Sinha, P. K. (1991). Hygrothermal effects on the bending characteristics of laminated composite plates. Computers & Structures, 40(4), 1009-1015. https:// doi.org/10.1016/0045-7949(91)90332-G

[12]. Shojaee, S., Valizadeh, N., Izadpanah, E., Bui, T., & Vu, T. V. (2012). Free vibration and buckling analysis of laminated composite plates using the NURBS-based isogeometric finite element method. Composite Structures, 94(5), 1677-1693. https://doi.org/10.1016/j.compstruct.20 12.01.012

[13]. Université Libre de Bruxelles (ULB). (n.d.). Hygrothermal stresses in laminates [Powerpoint Presentation]. Retrieved from https://scmero.ulb.ac.be/ Teaching/Courses/MECA-H-406/H-406-6-Hygrothermal.pdf

[14]. Thai, C. H., Rabczuk, T., & Nguyen-Xuan, H. (2013). A rotation-free isogeometric analysis for composite sandwich thin plates. International Journal of Composite Materials, 3(6A), 10-18.

[15]. Zenkour, A. M., & Alghanmi, R. A. (2016). Bending of symmetric cross-ply multilayered plates in hygrothermal environments. Mathematical Models in Engineering, 2(2), 94-107. https://doi.org/10.21595/mme.2016.17405