Table 1. Input Parameters for Group - I
This study focuses on the Artificial Neural Network (ANN) model for predicting the performance of Fibre Reinforced Polymer (FRP) strengthened High Strength Concrete (HSC) beams under cyclic load. The data required for ANN modelling is collected from relevant literature. Back propagation network with Levenberg–Marquardt, Bayesian Regularization and Scaled Conjugate Gradient were chosen for the proposed network, which is implemented using the programming package MATLAB. In the present study, the experimental results were obtained for FRP strengthened HSC beams under cyclic load applied by Push pull jack and Actuator. The investigation has been performed by comparing the test results with the results predicted by the neural network and the regression modeling. The accuracy of the proposed model has been ascertained using statistical indicators such as RMSE, R² and MAE. The scatter plots are drawn for ANN and regression results. Comparing the proposed results with existing experimental results exhibits very good convergence.
Strengthening of high strength concrete (HSC) members and fibre reinforced concrete (FRC) members with externally bonded fibre reinforced polymer (FRP) laminates is an effective and convenient method to improve their static and fatigue performance under service loads or ultimate loads. The design of structural strengthening applications using externally bonded FRP composites is usually based on conventional design approaches with the improvement of the presence and characteristics of the FRP material.
Suguna et al. (2018) predicted an artificial neural network based model for predicting the performance of high strength concrete beams strengthened with surface mounted FRP laminates. Back propagation network with Levenberg-Marquardt algorithm has been chosen for the proposed network implemented using the programming package MATLAB. MAE and RMSE were found to be acceptable. The statistical indicators such as correlation co-efficient (r) and co-efficient of determination (R2) were also predicted to estimate the accuracy of results obtained through ANN modeling. The results predicted through ANN model exhibited good correlation with the experimental results.
Hashemi et al. (2007) presented the finite element and experimental serviceability analysis of HSC beams strengthened with FRP sheets. The finite element analysis using ANSYS was performed to examine the structural behaviour of tested beams. A comparison between finite element analysis and experimental data was made by trial and error method.
Paturi et al. (2018) proposed an application of regression and ANN analysis in modeling of surface roughness in hard turning of AISI 52100 steel. The surface roughness predictions using RA and ANN models were deported in reasonable agreement when compared to the surface roughness values determined experimentally.
Shanmugavelu et al. (2016) presented the experimental and analytical studies on RC beam with GFRP laminates. The model was developed using general regression neural network (GRNN) to predict different target parameters such as yield load, deflection at yield load, ultimate load, deflection at ultimate load and ductility ratio respectively.
Perera et al. (2010) predicted the ultimate strength of RC beams FRP strengthened in shear using neural networks. The results through neural networks performed well on comparing with experimental results.
Pannirselvam et al. (2010) proposed an ANN model for performance evaluation of RC rectangular beams with externally bonded GFRP sheets. The results of 15 reinforced concrete beams with an ANN based model was reported. Three input parameters such as percentage (%) of steel reinforcement, thickness, and type of fibers were selected for the model.
Amani and Moeini (2012) predicted shear strength of RC beams using ANFIS and ANN. Back-propagation algorithm was used to predict the shear strength of RC beams.
Fathalla et al. (2018) presented remaining fatigue life assessment of in-service road bridge decks based upon ANN. An ANN model was strictly trained by the integrated lifetime simulation system. The proposed ANN model offers a speedy assessment of remaining fatigue life of insitu RC bridge road decks in service based on their bottom surface cracks inspected. Thus, bridge maintenance works will be efficiently supported without running the 3D non-linear multi scale simulation programs.
The above authors reported that ANFIS, ANN and regression models provided most appropriate prediction results of the target parameters. The present study has an aim to develop ANN and regression model to analyze the behavior of Fibre Reinforced Polymer strengthened High Strength Concrete beams.
In this comprehensive study, a large database containing the test results of 119 FRP strengthened HSC beams under cyclic load applied by Push pull jack and Actuator were obtained and listed out in group I and group II respectively. The beams under cyclic load applied by Push pull jack consist of 63 test results collected from 8 different investigations. (Daniel & Loukili, 2002; Dagenais & Massicotte, 2017; Fang et al., 1993; Gopinathan et al., 2016; Hashemi et al., 2007; Hassan & Mhebs, 2018; Krishnamurthy et al., 2016; Seshadrisekhar et al., 2015; 2016; Sethuraman et al., 2017).
The beams under cyclic load applied by Actuator consist of 56 test results collected from 4 different investigations (Kwak & Park, 2001; Raj et al., 2015; Rezansoff et al., 1993; Thandavamoorthy, 1999).
The basic steps for the development of ANN model are as follows:
An extensive literature review has been carried out for fiber reinforced polymer strengthened high strength concrete beams under cyclic load. The input and target parameters for Group I are presented in Table 1 and Table 2, respectively for fiber reinforced polymer strengthened high strength concrete beams under cyclic load applied by Push pull jack.
Table 1. Input Parameters for Group - I
Table 2. Target parameters for Group - I
The input and target parameters for Group II are presented in Table 3 and Table 4, respectively for fiber reinforced polymer strengthened high strength concrete beams under cyclic load applied by Actuator.
Table 3. Input parameters for Group - II
Table 4. Target Parameters for Group - II
In this stage, the input data was divided into three groups as train data, validate data and test data. The step wise procedure for ANN modeling is represented in Figure 1 to Figure 3.
Figure 1. Neural Network Fitting Tool Set Up
Figure 2. Importing the Input and Target Parameters
Figure 3. Selection of Training, Validation and Testing Data
The architecture of neural network proposed model is shown in Figure 4.
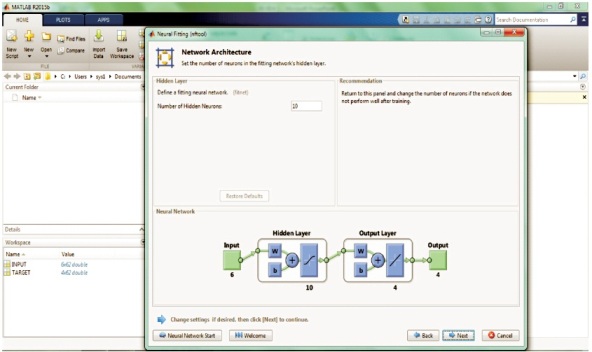
Figure 4. Neural Network Architecture
Back propagation with Levenberg-Marquardt algorithm, Bayesian Regularization algorithm and Scaled Conjugate Gradient algorithm were used to develop the artificial neural network. The training processes are shown in Figure 5.
Figure 5. Training Network
The fitness of the developed model is shown in Figure 6 to Figure 9.
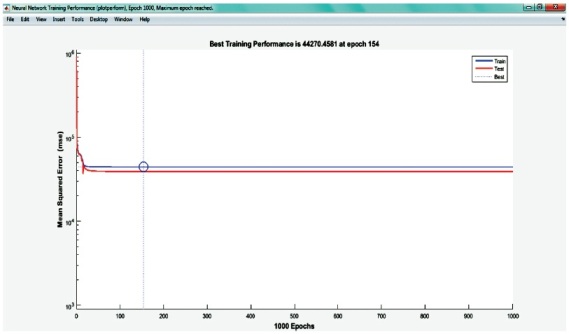
Figure 6. Performance Plot
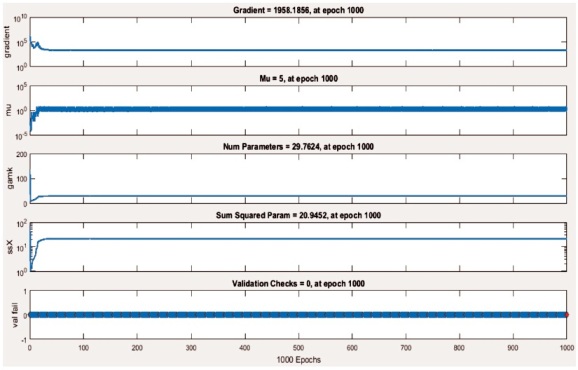
Figure 7. Training State
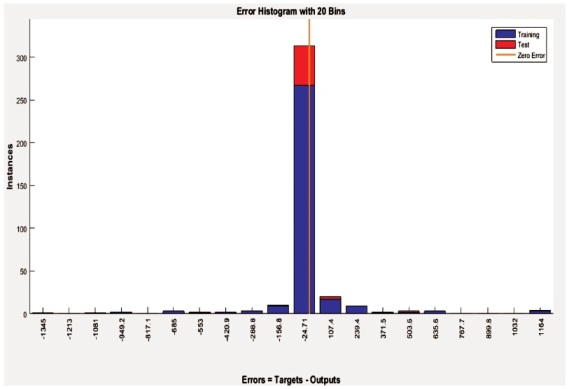
Figure 8. Error Histogram
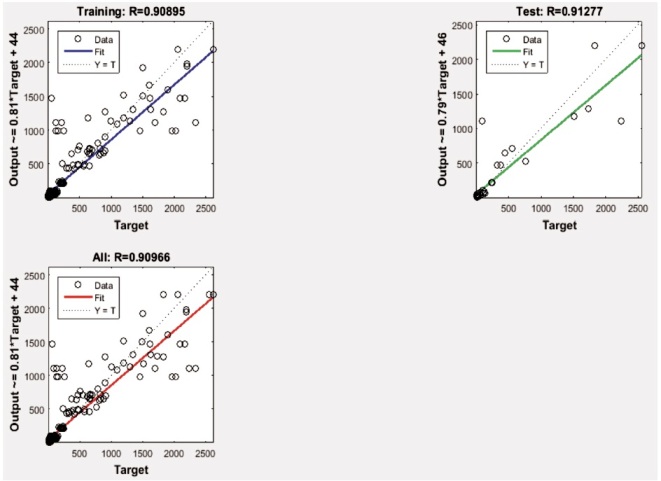
Figure 9. Regression Plot
Initially, the ANN network was trained with experimental procedure from the available literature. Three algorithm functions were used in ANN inputs. After the training process, the ANN networks were tested to determine the number of cycles, yield load, deflection, displacement ductility and stiffness. According to the experiments, the input parameters such as breadth (b), depth (d), % of steel, characteristic strength of concrete (fck), FRP thickness (t) and As'/As were used. The final outputs include the number of cycles, yield load, deflection, displacement ductility and stiffness and the same were verified using MATLAB ANN Toolbox. Figure 6 to Figure 9 shows the ANN performance plot, training state and error histogram for Levenberg Marquardt algorithm. Almost the same trend had been noticed for other algorithms. The predicted values using the ANN model are shown in Figure 10 in the form of scatter plots. The prediction of ANN results are in very good correlation with the measured experimental results. This observation can be confirmed with very high value for the coefficient of determination. Consequently, it is obvious that the predicted values enjoy a high level precision.
Figure 10. Scatter Plots for (a) No of Cycles (b) Yield Load (c) Deflection (d) Displacement Ductility (e) Stiffness
The performance of the ANN model for estimating the number of cycles, yield load, deflection, displacement ductility and stiffness were evaluated according to the statistical criteria, such as RMSE, coefficient of determination (R2) and MAE. The ANN model outperformed according to the results in Table 5. The ANFIS model provides significantly better results because of the higher ANN accuracy is related to the adaptability of the ANN network. All the algorithms have been used in ANN modeling.
Table 5. Statistical Indicators
On the basis of the comparison of RMSE, R2, and MAE, it may be concluded that the proposed ANN model performed well in predicting the experimental results.
In addition to neural network, a multiple regression-based model was proposed to evaluate the fiber reinforced polymer strengthened high strength concrete beams under cyclic loading. For comparative purpose, the experimental data were analysed by a licensed multiple regression software package Originpro®. The experimental data on fiber reinforced polymer strengthened high strength concrete beams under cyclic loading were imported directly from Microsoft® Excel. The linear regression analysis was then conducted. Regression models were solved and automatically sorted according to the goodness-of-fit criteria into a graphical interface on the Originpro®.
In this study, various important statistical indicators, such as coefficient of determination (R2), Mean Absolute Error (MAE), Root Mean Square Error (RMSE) were computed to quantify the fit between experimental data and model outputs. The regression equations are presented in Table 6.
Table 6. Regression Analysis