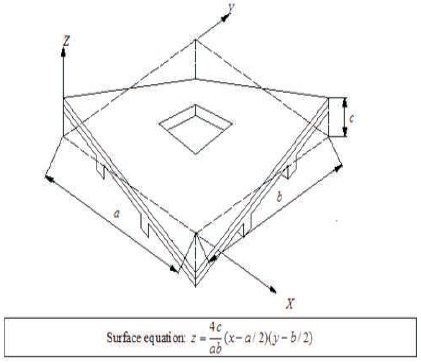
Figure 1. Surface of a Skewed Hypar Shell with Cut-out
Laminated composite shells are used as roofing units in Civil Engineering applications and hypar shells are most popular because of their ease of construction and aesthetic elegance. The aim of the present study is to analyse higher mode free vibration of composite hypar shells. The purpose is to obtain some design guidelines for the practising engineers dealing with such structures. The methodology adopted here is the finite element method based on first order shear deformation theory. Effect of cross curvature is included in the formulation. The isoparametric finite element consists of eight nodes with five degrees of freedom per node is considered. Three noded beam elements with four degrees of freedom per node are used for stiffeners. The generalised Eigen value solution is chosen for the un-damped free vibration analysis. The formulation is validated first by solving standard problems from literature and then new results are obtained for varying boundary conditions, ply orientation and curvature of the shell. The first five modes of natural frequency are presented. In general, it is observed that fundamental frequency increases with the increase in the number of support constraints. There are, however, few departures from this general tendency when two shells of different laminations are compared. Sometimes lamination order may influence the frequency of stiffened composite shell with cut-out more significantly than its boundary conditions. Symmetric lamination exhibits reasonably good performance and may be adopted for all practical purposes.
Laminated composite shell structures characterized by high strength/weight value and reduced dead weight are used in different structures of many engineering fields like civil, mechanical, aerospace and others. In civil engineering application laminated composite shells are used as roofs as these can cover large column free areas. Among the different shell configurations, hypar shell (hyperbolic paraboloid shell bounded by straight edges) is very popular as roofs due to their aesthetic elegance (Figure 1). The shell surface being doubly ruled, it is very easy to construct and construction becomes faster. Roofs are often provided with cutout for entry of light, venting and at times to provide accessibility of parts of the structures, and to alter the resonant frequency. Shells with cutout, stiffened along the margin are an efficient way to enhance the stiffness of the structure without adding significant mass. These stiffeners slightly increase the weight but have larger effect on structural strength and stability. In practice, shell roofs may have different combinations of boundar y conditions and a comprehensive study of free vibration characteristics of such structures is of practical interest.

Figure 1. Surface of a Skewed Hypar Shell with Cut-out
A finite element model has been used in the present study for free vibration analysis of composite stiffened hypar shell with cut-out on higher modes. The analysis has been performed considering shallow shell assumptions. The effect of cross curvature is also included in the formulation. The present finite element model based on first order shear deformation theory is applied to solve many practical problems of laminated composite stiffened hypar shells considering different boundary conditions, laminations and shell geometry.
Some of the earlier information regarding the behaviour of doubly curved composite shells was reported by Narita and Leissa (1984) and Reddy and Chandrashekhara (1985) who considered the practical boundary conditions like corner point support and presented the frequency and mode shapes of spherical, circular cylindrical and hyperbolic paraboloidal (bounded by parabolas) shells. Liew, Kitipornchal, and Wang (1993) analysed plates and shells for bending, buckling and vibration behaviour using a super element. Point supported boundary conditions, were also considered by (Schwarte, 1994; Chakravorty, Bandyopadhyay, & Sinha, 1995). In two consecutive papers, Qatu and Leissa (1991a, 1991b) have studied the free vibration behaviour of doubly curved laminated composite shallow shells. Qatu and Leissa (1991c) and Sivasubramonian, Kulkarni, and Rao (1997) studied the free vibration characteristics of doubly curved panels considering combinations of different boundary conditions. Liew and Lim (1994a, 1994b, 1996); Lim and Liew (1994, 1995a, 1995b); Liew, Lim, and Ong (1994a, 1994b) carried out extensive research work on the vibrations of different types of shell surfaces. The developments in the vibration of shallow shells reviewed in an excellent paper by Liew, Lim, and Kitipornchai (1997). The fundamental frequencies of hypar shells with different boundary conditions were reported by (Chakravorty, Sinha, & Bandyopadhyay, 1998; Sahoo & Chakravorty, 2005). Pradyumna and Bandyopadhyay (2008) reported the vibration characteristics of composite hypar shells based on HSDT but they did not considered higher modes, hence further improvement in these results have to be sought.
Noteworthy research articles on shell studies are by (Rikards, Chate, & Ozolinsh, 2001; Nayak & Bandyopadhyay, 2002a, 2002b, 2005, 2006; Sahoo & Chakravorty, 2005, 2006; Kumar, Chakrabati, & Bhargava, 2013, 2015; Bhargava, & Chakrabarti, 2012; GulshanTaj & Chakraborty, 2013; Tornabene, Fantuzzi, Bacciocchi, & Dimitri, 2015; Dey, Bandyopadhyay, & Sinha, 1992; Dey, Mukhopadhyay, & Adhikari, 2015; Zhang, Jin, Ma, & Ye, 2016). Sahoo (2012, 2013, 2014a, 2014b, 2015a, 2015b, 2016, 2019) have studied the free vibration aspects of stiffened shell panel with cut-out for six shell forms, viz., cylindrical, elliptic paraboloid, hyperbolic paraboloid, hypar, conoid, and spherical shells using finite element method. But analysis of stiffened shell with cut-out for higher mode is scanty in the literature. (Topal, 2006; Tornabene, Fantuzzi, Bacciocchi, & Dimitri, 2015) have presented the mode frequency analysis of laminated spherical shell but they did not consider hypar shells.
Thorough literature review reveals that there is no literature available on free vibration analysis of composite stiffened hypar shells with cut-out for higher modes. Accordingly, a finite element model has been used in the present study to analyse free vibration behavior of composite stiffened hypar shell with cut-out on higher mode and to obtain some design guidelines for the practising engineers dealing with such structures.
A laminated composite hypar shell of uniform thickness h (Figure 1) and twist radius of curvature Rxy is considered. For same total thickness, the thickness may consist of any number of thin laminae each of which may be arbitrarily oriented at an angle with reference to the X-axis of the coordinate system. An eight-noded curved quadratic isoparametric finite element (Figure 2a) is used. The five degrees of freedom taken into consideration at each node include two in-plane and one transverse displacement and two rotations about the X and Y axes. Sahoo and Chakravorty (2005) have reported the strain-displacement and constitutive relationships together with the systematic development of stiffness matrix for the shell element. Three noded curved isoparametric beam elements (Figure 2b) are used to model the stiffeners, which are taken to run only along the boundaries of the shell elements. In the stiffener element, each node has four degrees of freedom, i.e., usx, wsx, αsx, and βsx for X- stiffener and usy, wsy, αsy, and βsy for Y-stiffener. The generalized force-displacement relation of stiffeners can be expressed as (the notations have been defined in the nomenclature):
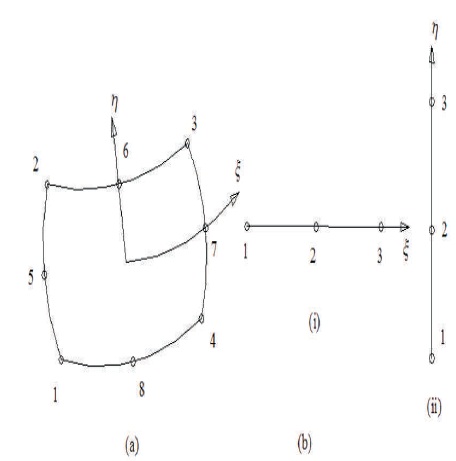
Figure 2. (a) Eight Noded Shell Element (b) Three Noded Stiffener Element (i) X-stiffener (ii) Y-stiffener
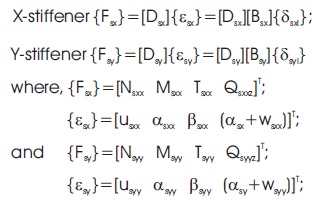
Elasticity matrices are as follows:

and Aij, Bij, Dij, and Sij are explained in an earlier paper by Sahoo and Chakravorty (2005). Detailed formulation is available elsewhere (Sahoo, 2019). The effect of eccentricities of stiffeners also included. The element stiffness matrices are of the following forms.
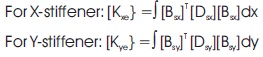
The integrals are converted to isoparametric coordinates using 2-point Gauss quadrature. Finally, the element stiffness matrix of the stiffened shell is obtained by appropriate matching of the nodes of the stiffener and shell elements through the connectivity matrix and is given as:
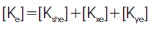
The element stiffness matrices are assembled to get the global matrices. The element mass matrix for shell is obtained from the integral,

where,
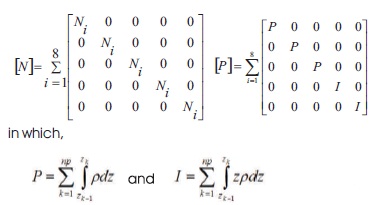
Element mass matrix for stiffener element:
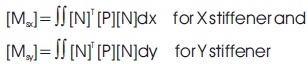
Here, [N] is a 3x3 diagonal matrix
for X-stiffener
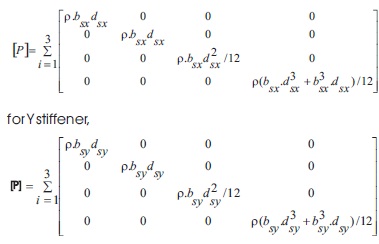
The mass matrix of the stiffened shell element is the sum of the matrices of the shell and the stiffeners matched at the appropriate nodes.
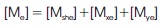
The element mass matrices are assembled to get the global matrices.
The free vibration analysis involves determination of natural frequencies from the condition,
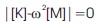
This is a generalized Eigenvalue problem and is solved by the subspace iteration algorithm. Subspace iteration is a simple method for approximating Eigenvalues and Eigenvectors of matrices. It can be seen as a generalization of the Power Method, in the sense that it iterates simultaneously on multiple initial vectors, instead of just one. Orthogonality of the vectors is explicitly enforced in order to avoid linear dependence as the iteration proceeds.
The position and size of cut-out is supplied as input in the code, which is capable of generating non uniform finite element mesh all over the shell surface. Element size is gradually decreased near the cut-out margins. Figure 3 shows one typical mesh. Such mesh is refined in steps and a particular grid is chosen to obtain the fundamental frequency, when the result does not improve by more than one percent on further refining. Convergence of results is ensured in all the problems considered here.
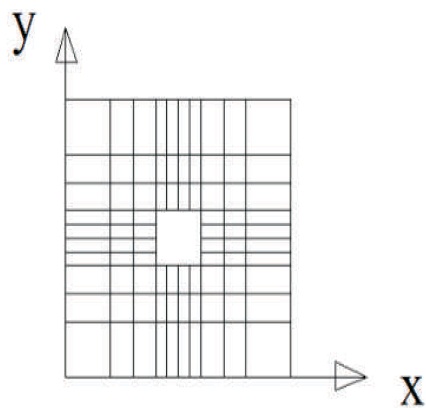
Figure 3. Typical 10x10 Non-uniform Mesh Arrangement Drawn to Scale
From Table 1, the agreement of present results with the earlier ones is excellent and the correctness of the stiffener formulation is established. Free vibration of simply supported and clamped hypar shell with (0/90)4 shell with cut-outs is also considered. The fundamental frequencies of hypar shell with cut-out obtained by the present method agree well with those reported by Chakravorty et al. (1998) as evident from Table 2, establishing the correctness of the cut-out formulation. Thus it is evident that the finite element model proposed here can successfully analyse vibration problems of stiffened skewed hypar composite shells with cut-out which is reflected by close agreement of present results with benchmark ones.
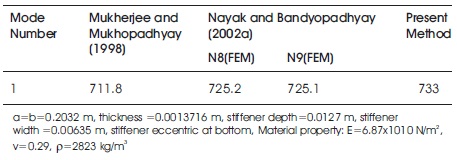
Table 1. Natural Frequencies (Hz) of Centrally Stiffened Clamped Square Plate
Table 2. Non-dimensional Fundamental Frequencies () for Hypar Shells (Lamination (0/90) ) with Concentric Cut-outs
Laminated composite stiffened hypar shells with cut-out is analysed to study the behaviour of the shell under free vibration at higher mode for different parametric variation. The cut-outs are placed concentrically on the shell surface. The stiffeners are placed along the cut-out periphery and extended upto the edge of the shell. The material and geometric properties of the shells are, a/b=1, a/h=100, a'/b'=1, a'/a=0.2, c/a=0.2, E11 /E22 =25, G23 = 0.2E22, G13 = G12 = 0.5E22, v12 =v21 =0.25, ρ=100 N- sec2/m4 unless otherwise specified. Different types of symmetric and antisymmetric cross and angle ply laminates with different lamination angle is considered.
The different boundary conditions, which are used in the present analysis are CCCC, CCSS, SSCC, CSCS, SCSC, SSSS, CCFF, FFCC, and CFCF. The boundary conditions are designated as, C for clamped, S for simply supported and F for free edges. The four edges are considered in an anticlockwise order from the edge x = 0. For example a shell with CSCS boundary is clamped along x = 0, simply supported along y = 0 and clamped along x = a and simply supported along y = b. Numerical analyses are also performed to determine the effect of curvature on non-dimensional frequency by varying c/a = 0.2, 0.15, 0.1 and 0.05.
Table 3 presents the non-dimensional frequencies for shells with different laminations and boundary conditions. To facilitate the interpretation of results the boundary conditions are divided into three groups. Group I consists of commonly encountered edge conditions which are clamped and simply supported. Each of the boundary conditions included in either of Group II and Group III has equal number of support constraints. On examining the results it is evident that the frequencies for all the laminations for all the modes depend on the number of boundary constraints. With increase in number of boundary constraints frequencies increase. Further it is noticed that for two layered laminates for Group I boundary conditions, angle ply shells show better performance than cross ply laminates but reverse is the case for Group III shells. For Group II shells cross ply shells show better performance on lower mode and angle ply shell shows better performance on higher mode. It is also evident from Table 3, that with increase in number of layers angle ply shells perform better than their cross ply counterpart, except some few cases. This is true for Group I and Group II shells but for group III shells except a very few cases cross ply shells are better choices. These are true for both fundamental and higher mode.
Table 3. Non-dimensional Frequencies for different Laminations of Laminated Composite Stiffened Hypar Shell with Cut-out for different Boundary Conditions on Higher Mode
Among Group II boundary condition although CCSS and SSCC perform better than CSCS and SCSC shells in lower mode but reverse is the case on higher mode. A more careful observation suggests that among Group III shells when number of layers are less CCFF and FFCC perform better but with increase in number of layers performance of CFCF shells are improved. Hence lamination order may influence the frequency of stiffened composite shell with cutout more significantly than its boundary conditions.
The mode shapes corresponding to the first five modes of vibration are plotted in Figure 4 for cross ply and angle ply shells respectively. The normalized displacements are drawn with the shell mid-surface as the reference for all the support condition and for all the lamination used here. The fundamental mode is clearly a bending mode for all the boundary condition for cross ply and angle ply shell. At higher modes of vibration mode shape do not change to a great extent. Most of the mode shapes are in bending mode. It is found that for higher mode, nature of the mode shapes is somewhat similar, only the crest and trough position changes.
Figure 4. Mode Shapes for Cross Ply and Angle Ply Shells for different Boundary Conditions for first five Modes
Table 4 contains the non dimensional frequency values for different symmetric laminates by varying the lamination angle and boundary conditions. It is observed from the results, with the increase in number of layers frequencies increase marginally from three layered to four layered shells. But with further increase in number of layers does not come to any effective benefit except CSCS and CFCF shells. This is expected as increasing the number of layers will result in reduced bending-stretching coupling and will increase the shell stiffness, till on increasing the number of layers the material becomes quasi-isotropic. Beyond that, increase in the number of layers will not improve the frequency to any extent. Rather, (0/θ)s lamination exhibit reasonably good performance and may be adopted for all practical purposes. It is also o observed that except for CCCC shells, where θ=45o yields the highest values of frequency but for all other boundary conditions frequency increases with θ. For CCSS and CSCS shells θ=60o either gives the highest frequency or yields a frequency value, which is marginally less than the highest one. Similarly for SSSS shells θ=75o and for CCFF and CFCF shells θ=90o gives the highest results. Figure 5 represents the mode shape corresponding to symmetric cross ply and angle ply laminated composite stiffened shells with cutout for fundamental and higher mode.
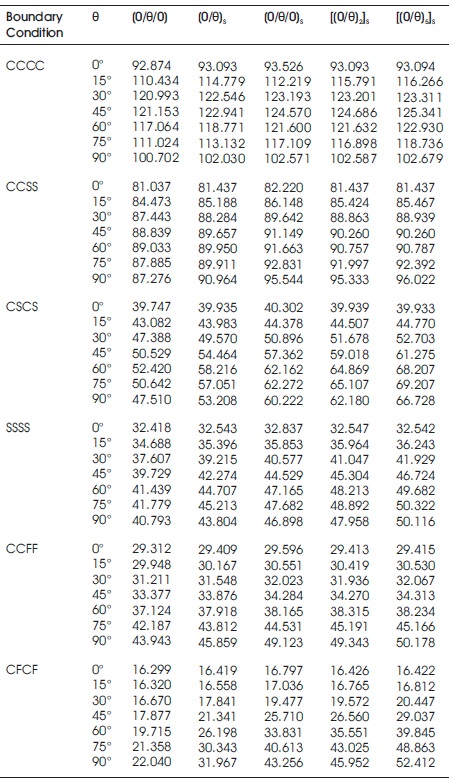
Table 4. Non-dimensional frequencies for symmetric laminated composite stiffened hypar shell with cut-out with different boundary condition
Figure 5. Mode Shapes of Symmetric Cross Ply and Angle Ply Shells with Cut-out for first five Modes
The frequencies of four layered symmetric and antisymmetric laminates are furnished in Table 5 for various lamination angles and boundary conditions. Since four layered laminates are very common in industrial applications, Table 5 is expected to be a good design aid for practicing engineers. Examining the frequencies of shells with four layered symmetric and antisymmetric stacking orders presented in Table 5, it is found that for CCFF, CFCF, and CCSS shells with 0/θ/0/θ stacking order the vibrational stiffness increase monotonically with θ. But for CCCC, CSCS, SSSS, and 0/ θ/ θ/0 CCSS shells, the frequency increases with θ upto a certain value but decreases when θ is further increased. Such decreases are quite marginal in all of these cases. All these observations are true for the first five modes shown here except very few cases. Out of twelve cases considered here in four cases (for CCFF, CFCF, and CCSS shells with 0/θ/0/θ) highest frequencies are found to be at θ=90o. In another eight cases highest frequencies are o found to be at θ=60o.
Table 5. Non-dimensional Frequencies for Composite Stiffened Hypar Shell with Cut-out with 0/θ/0/θ and 0/θ/θ/0 Lamination Scheme and different Boundary Conditions on Higher Mode
When performances of antisymmetric and symmetric laminates are compared, it is found that considering all the modes performance of antisymmetric laminate is better than its symmetric counter part. The only exception is symmetrically laminated CCCC shell with lamination angle 15o. For this shell symmetric laminate perform better than the antisymmetric laminate in all five modes shown here. Figure 6 represents the typical mode shapes corresponding to symmetric and anti symmetric cross ply and angle ply laminated composite stiffened shells with cutout for fundamental and higher mode.
Figure 6. Mode Shapes Corresponding to Anti symmetric and Symmetric Laminated Composite Stiffened Hypar Shell with Cut-out for different Boundary Conditions for first five Modes
The frequencies of 0/θ/θ/0 laminates are presented in Table 6 for various lamination angles with different c/a ratio for CCSS boundary condition. It is observed in general that frequency of each mode first increases with lamination angle then decrease for all c/a ratios. From Table 6 it is also observed that for CCSS boundary condition for a given lamination angle increase in c/a ratio increases the frequency of each mode. Figure 7 represents the typical mode shapes corresponding to fundamental and higher mode for symmetric angle ply laminated composite stiffened shells with cutout for different c/a ratio.
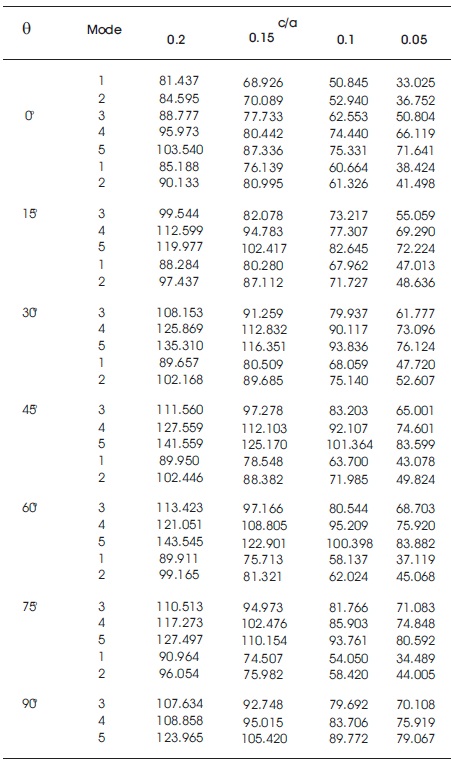
Table 6. Non-dimensional Frequencies w for 0/θ/θ/0 Stiffened Hypar Shell with Cut-out with different c/a Ratio for CCSS Boundary Condition on Higher Mode

Figure 7. Mode Shapes Corresponding to 0/45/45/0 Laminated Composite Stiffened Hypar Shell with Cut-out for CCSS Boundary Condition for different c/a Ratio for first five Modes
Higher mode free vibration analysis of composite hypar shells is presented using finite element method based on first order shear deformation theory and including the effect of cross curvature. In general fundamental frequency increases with the increase in the number of support constraints. There are, however, few departures from this general tendency when two shells of different laminations are compared. Sometimes lamination order may influence the frequency of stiffened composite shell with cut-out more significantly than its boundary conditions. (0/θ)s lamination exhibit reasonably good performance and may be adopted for all practical purposes. For four layered laminates the frequency either increases monotonically with θ or increases with θ upto a certain value of θ then decreases. For CCCC, CSCS, SSSS and 0/ θ/ θ/0 CCSS shells, the frequency increases with θ upto a certain value but decreases when θ is further increased. For each of these shells the values of θ yielding highest frequencies are to be found out by numerical experimentation. All these observations are true for the first five modes except very few cases. Considering all the modes performance of four layered antisymmetric laminate is better than its symmetric counterpart, except CCCC shell with lamination angle 15o. For shell with CCSS boundary condition for a given lamination angle increase in c/a ratio increases the frequency of each mode.
