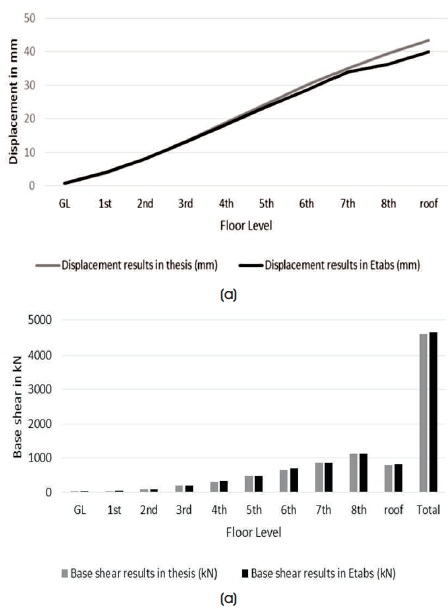
Figure 1. (a) Displacement and (b) Base Shear Results
Now, in current practice, the whole world is in the race of looking forward to earn maximum profit. A structural engineer's goal is to prepare an ideal cost effective solution for the design of structure for any construction project. In this paper, the present work deals with the aim of achieving the optimal and ideal design of reinforced concrete structures, reducing size and reinforcement for beam members and column members in multi - bay and multi - storey structures. Generally, it is a practice to optimize cost by trial and error method, which is used in a number of software likes STAAD PRO, ETABS, STRUDS, etc. But this method is quite complex and has less accuracy thus there is a need to adopt one proper optimization technique which enables engineer to find and to prepare the ideal design for the structure which gives more accuracy. So, in this paper, for cost optimization of Reinforced Concrete (RC) framed structure, MINLP (Multi- Integer Non-Linear Programming) technique is adopted. Without changing the functional criteria of beams and columns as per provisions given in IS456-2000, the structure is designed and assuring economically safety. Programming of the design of structural elements beam and column has been done using MATLAB program. At the end of the study, the results of the optimized model using MINLP technique and manually optimized method are compared. This optimization task reduces 24.76% of the total approximate cost in beams and 13.79% in columns.
Optimization in Reinforced Concrete (RC) structural design, as a primary building material component, attracted attention of design engineers, researchers, and professional engineers. Literature on RC design shows significant efforts in the optimization of concrete components and mixture proportions (Guerra & Kiousis, 2006; Balling, 1993; Ganju, 1996). Early reinforced concrete design procedures, including the mixture proportions, were based on repeated trials from which an appropriate and acceptable design and proportion were selected. For optimization the relationships established were mainly between the mix composition and the compressive strength (Balling, 1993).
Although in concrete design and mixture proportions, optimization methods are frequently applied, few of these methods consider the costs of both plain concrete and reinforcement as functions.
Cost optimization stays one of the major factor in construction projects. It is the obligation of all individual members of the structure design team to think about diagnostic procedures for cost optimization. Maximum effect to be gained on expenses and cost is accessible at the earliest parts in the life cycle of a construction project (Goodchild & Lupton, 1999). The RC system is the major area which allows great contribution to achieve cost optimization; specifically during the design phase.
One aspect of reducing cost during structure design comes with an introduction of the Design-To-Cost method (Deaton, 2005). The principle of Design-To-Cost is to prepare design converge on expenses and costs, instead of the other way around. In the case of value engineering Design-To-Cost has downsides of additional time and cost of redesigning/re-bidding, and the compromise of quality. In India, for cost optimization in RC design, no systematic procedure has been adopted.
Most structural design consulting offices do not advocate realistic estimate of material costs, even though all the specifications set forth by design codes are satisfactorily incorporated. The practical uses of cost optimization in RC design are still relatively uncommon, and they are normally dependent on manual and continuous trials of design. Design consulting offices have the most difficult task of convincing their clients or owners of the cost efficiency of their structure designs (Goodchild & Lupton, 1999; Kulkarni & Rojiani, 1994).
The upsides of computer technology have been incorporated in the optimization of RC structure design and mixture proportions; most notably is the utilization of spreadsheets. Spreadsheets are easy to use and exceedingly powerful, however, are not being taken in use as much as they could be in structural design engineering (Kwakye, 1997). Spreadsheets and smart databases are being utilized for mix designs (de Larrard & Sedran, 1996; Brandt, 1998) and computerization of concrete design (Guerra & Kiousis, 2006; Mather & Rashwan, 1997). Other approaches utilized for RC design and mixture proportions for example, constraint-based reasoning (Regupathi, 2017) and object-oriented (Lucas & Roddis, 1996) can utilize the programming tools such as VISUAL BASICS, MATLAB, FORTRAN and C++.
In order to understand the latest trends and ongoing research development – a focused survey of the white papers, technical articles and journals was performed. Following is the summary of few of the relevant and important papers in the field of optimization of RCC structures.
James B. Deaton from Georgia Institute of Technology in Aug 2005, elaborated the details in “A finite element approach to Reinforced Concrete Slab Design”. In this work, he explains step by step development of a procedure in GT STRUDL to design reinforced concrete flat plate system. Babiker, Adam, and Mohamed (2012) studied design of reinforced concrete flat plate system using finite element analysis. The current state-of-practice of reinforced concrete flat plate design was reviewed, including the ACI (American Concrete Institute) direct design and equivalent frame techniques, the yield line method, and the strip design method. Additionally, the current state-of-the-art of flat plate design based on finite element results was presented, along with various flat plate modeling techniques. Design methodologies studied included the Wood and Armor approach, based on element stress resultants, and the resultant force approach, based on element forces (Deatox, 2005). Design examples presented include single-panel flat plate systems with various support conditions as well as multi-panel systems with regular and irregular column spacing. The examples additionally showed that when cuts were not oriented orthogonally to the directions of principle bending, resulting designs based on element forces could significantly under reinforce the cross-section due to significant torsional effects.
Another paper presented by Andres Guerra and Panos Kiousis from Colorado School of Mines, USA titled “Design optimization of reinforced concrete structures” discusses a novel formulation aiming to achieve optimal design of Reinforced Concrete (RC) structures is presented here (Umar, Ahmad, Ahmad, & Huda, 2017). Optimal sizing and reinforcing for beam and column members in multi-bay and multistory RC structures incorporates optimal stiffness correlation among all structural members and results in cost savings over typical-practice design solutions. A Nonlinear Programming algorithm searches for a minimum cost solution that satisfies ACI 2005 code requirements for axial and flexural loads. Material and labor costs for forming and placing concrete and steel are incorporated as a function of member size using RS Means 2005 cost data. Successful implementation demonstrates the abilities and performance of MATLAB's Sequential Quadratic Programming algorithm for the design optimization of RC structures. A number of examples are presented that demonstrate the ability of this formulation to achieve optimal designs.
Dimensional analysis of four types of buildings which are having four different sizes of shear walls have been carried out using ETABS 2016. Software results have been compared with thesis results, where maximum error in displacement results have been occupied 9.1% and in base shear 2.92%, which is as shown in Figure 1.

Figure 1. (a) Displacement and (b) Base Shear Results
The multi integer non-linear programming (MINLP) continuous optimization problem could be defined as:
Min. z = f(x)
subjected to:
h(x) = 0, g(x) ≤ 0
X ∈ X = {x | x ∈ Rn, XL ≤ x ≤ xU}
where, x is a vector of continuous variables, which is defined within the compact set X.
Functions f(x), h(x) and g(x) are nonlinear functions included in the objective function z, equality and inequality constraints, respectively.
All the functions f(x), h(x) and g(x) must be continuous and differentiable.
In the circumstance of an optimization, the vector of continuous variables indicates entities whose values are commonly unknown until after the model has been solved. These are different parameters of a structure, for example, loads, forces, dimensions, materials, stresses, cross section characteristics, deflections, economic parameters, and so on. An appropriate estimations of the taken variables are acquired when the minimum value of the predefined objective function is matched. The system of an inequality and equality constraints and the bounds of the variables show a rigorous system of design, stress, load, deflections and resistance functions derived from structural analysis and design codes (Vitaliano, 1994).
The quantities of materials for any construction project could be either calculated on the previous records of completed construction projects or alternatively from the first principles by structural analysis, structural design and quantities calculation (Walden, Lee, Wilkerson, & Steve, 1996). The theoretical system is to design RC structural elements depends on the cost of accessible materials and not just on the accessibility of materials as shown in Figure 2 (Young, 1997).
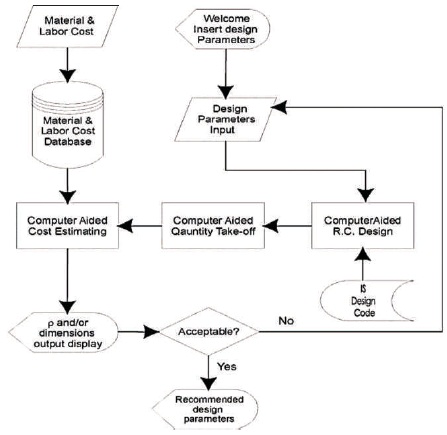
Figure 2. Suggested System for Cost Optimization of Reinforced Concrete Structure Element (Lucas & Roddis, 1996)
In an optimization task, few parameters could be taken as pre-assigned or fixed parameters where others are taken as design variables. The design variables are obtained so that a value of an objective function, which frequently reduces the cost of an element. Few limitations called the design constraints, may restrict the acceptable values of the design variables.
In this model the fixed parameters are the modulus of elasticity, characteristic strength, unit weight of reinforcement and concrete and the intensity of the live loads and deadloads.
The overall cost of the structure is determined by using fixed parameters to find cost of unit weight of reinforcement and unit volume of concrete.
The design variables which are taken in this RC beam model are:
The following Equations are the bounds taken for the model.
The design constraint which is taken in this optimization task are:
Mu ≤ φ Mn
S ≥ Smin
The objective function for optimized reinforced concrete beam problem is:
Minimumcost = Cc [(Ac - As)*L] + Cc [As *L)]
where,
A multi storey residential building having ground floor with seven floors is taken for an optimization. The floor plan beam grid is as shown in Figure 3. This project is situated in Ahmedabad which is having medium soil. The building design is satisfying to structural design criteria as per IS:456-2000.
A model was created in STRUDS-GT 2009 as per the dimension of the plan for the structural analysis. While preparing the model, followings are the considered:
In addition to optimization model using MATLAB, one more model is also created for the design and cost optimization of RC beam and column using Excel spreadsheets.
The Generalized Reduced Gradient (GRG) method is considered in the Excel spreadsheet to run the optimization process.
In given example, all beams and columns at different floor level have been optimized in MATLAB and EXCEL SOLVER, where it reduces the total cost of beam by Rs.740319.23 and column Rs.350103.50 as compared to the actual cost.
Comparison of a single beam at different floor with its actual beam data and optimized beam data are as shown in Tables 1-9.
From Tables 1-9 of this optimization report of beams, it can be observed that the percentage of steel increases when the depth of beam has been reduced. And the overall average cost in all beams optimized up to 24.76%.
Comparison of column of different size at different floor with its actual column data and optimized column data are as shown in Table 10.
From this optimization report of column it can be observed that the percentage of steel increases when the depth of beam has been reduced. And the overall average cost in all beams optimized up to 13.79%.
Using MINLP optimization technique the optimum size of beam at plinth beam level is 300 mm x 450 mm and at typical floor level are 300 mm x 425 mm, 300 mm x 375 mm and 300 mm x 350 mm. Whereas the optimum size of columns are 230 mm x 1950 mm, 400 mm x 600 mm and 230 mm x 1350 mm.
After cost optimization process the most optimum section for beams and columns at different floor levels have been obtained. This optimization task reduce 24.76% of the total approximate cost in beams and 13.79% in columns. The results of this task are further verified for each and every element of the structure which is within the safety limit as per the guideline IS-456: 2000 Code.
It is also concluded that MINLP technique has more accuracy than trial and error method.