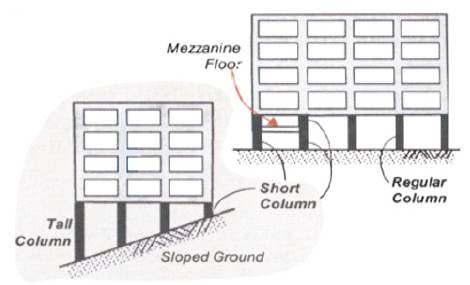
Figure 1. Buildings with short columns ( [5] )
An analytical study has been carried out to investigate the seismic behaviour of multi-storey buildings resting on normal and sloping grounds in different seismic zones with and without base isolators. Totally 160 multi-storey building models with rectangular configuration in plan of 12 x 16 m size have been analysed. The building models considered ranges from 1 storey height to 10 storey heights, and assumed to be located in seismic zones II, III, IV and V as per Indian standard code under two different terrain conditions viz. plain and sloping grounds with and without seismic base isolators. Response spectrum method of dynamic analysis has been performed using STAAD Pro software for all the building models, and the dynamic response quantities such as fundamental time period, base shear, top floor displacement and inter-storey drift were obtained for all the models. Seismic analysis results of building models indicate that for a given seismic zone and terrain condition, the introduction of seismic base isolators at base level of building increases fundamental natural time period, but reduce base shear, top floor displacement and inter-storey drift of the building. The results also indicate that for a given base (i.e. support) condition and terrain nature the base shear, top floor displacement and inter-storey drift increase as the seismic zone level increases. Furthermore, the results indicate that the introduction of seismic base isolation system at the base of building makes the structure behave like a rigid structure.
Analysis of buildings resting on a hill is different from analysis of buildings resting on normal (i.e. plain) ground, since the columns of hill buildings rest at different levels on sloping ground in hilly areas. The short columns of hill buildings attract more forces and undergo extensive damage if it is not properly designed for earthquake forces. Also, buildings on hills have mass and stiffness varying along the vertical/horizontal plane resulting in the centre of mass and centre of rigidity that do not coincide at various floor levels. Due to this, these irregular buildings experience torsion, in addition to bending and shear, during earthquake ground motion. Hence, these buildings which are irregular and unsymmetrical in nature require greater attention during the analysis and design stages.
During past earthquakes, reinforced concrete (RC) frame buildings constructed on hilly regions that had columns of different heights within a storey suffered more damage in the shorter columns than taller ones. When a building constructed on sloping ground experiences inertia force due to earthquake, all columns move horizontally by the same amount along with floor slab at a particular level (this is called rigid floor diaphragm action). If short and tall columns exist within the same storey level, then the short columns attract more earthquake force and suffer severe damage as compared to the taller ones. This is due to the fact that during an earthquake, a tall column and a short column of same cross-section move horizontally by same amount. However, the short column is stiffer as compared to the tall column, and it attracts larger earthquake force. Stiffness of a column means resistance to deformation - larger is the stiffness, larger is the force required to deform it. If a short column is not adequately designed for such a large force, it can suffer significant damage during an earthquake. This behaviour of column is called short column effect. The damage in these short columns is often in the form of x-shaped cracking, and this type of damage is due to shear failure. Figure1 shows the buildings with short columns, and Figure 2 shows the behaviour of short and long columns under lateral force.

Figure 1. Buildings with short columns ( [5] )
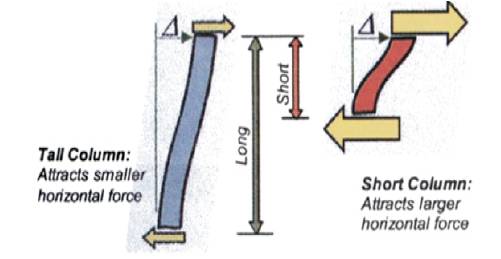
Figure 2. Behaviour of long and short columns [5]
Base isolation technique is one of the techniques used in the earthquake resistant design and construction of structures. This technique separates super-structure of building from its sub-structure, and prevents entry of ground acceleration into the building from the ground during earthquakes. The super-structure of an isolated building, under the action of earthquake force, acts like a rigid body with reduced inter-storey drifts, thus mitigating the subsequent seismic damage of the building. Also, the base isolation system reduces the fundamental frequency of the structure from its fixed base frequency, and thus shifts the position of the structure in the spectrum from the peakplateau region to the lower region as shown in Figure 3. In other words, the base isolation system increases the fundamental time period of the structure. Furthermore, the base isolation system brings additional damping due to the increased damping introduced at the base level, and thus further reduction in the spectral acceleration is achieved.

Figure 3. Plot of time period versus acceleration ( [16])
In the past, attempts had been made to study the seismic analysis of buildings either resting on normal ground or resting on sloping ground, either with seismic base isolator or without seismic base isolator, either for one seismic zone or for more than one seismic zone, either for one storey height or for more than one storey height ( [1], [2],[3], [4], [7], [8], [9], [10], [11], [12], [13], [14], [15], [16], [17] ). But in the present work, an analytical study has been carried out to investigate the seismic behaviour of 160 multi-storey building models resting on normal and sloping grounds in different seismic zones with and without base isolation system. The results obtained in this study are presented and discussed in this paper.
Table 1 shows the details of various building models considered in this study for seismic analysis. All the160 building models considered in this study were modelled as a 3D space bare frame structure and analysed using response spectrum method of dynamic analysis with help of STAAD Pro software. The models considered were assumed to be resting on normal and sloping grounds (18.43° with horizontal) with and without base isolators on four different seismic zones viz. II, III, IV and V as per IS 1893 code ( [6]). The various parameters used for modelling are: building is rectangular in plan and 12 m along X direction & 16 m along Y direction; type of structure is special RC moment resisting frame; cross-section of all columns is 400×500 mm and column height is 4 m in bottom storey & 3 m in all other storeys; cross-section of all beams is 400 x 500 mm and 4m center to center; thickness of slab is 120 mm; concrete grade is M 20 and steel grade is Fe 415;density of concrete is 25 kN/m3 ; Live load on roof is 2 kN/m2 and on floor is 4 kN/m2 ; response reduction factor is 5; importance factor is 1; damping is 5 %; type of soil is medium; seismic base isolator is lead rubber bearing (LRB) with vertical stiffness of 2700 kN/m and horizontal stiffness of 1125 kN/m ( [16]). The plan and elevation of building models are shown in Figures 4a to 4e.
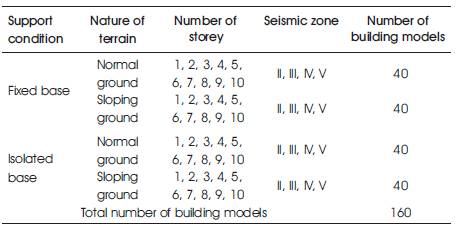
Table 1. Details of various building models

Figure 4a. Plan of building

Figure 4b. Elevation in X-direction - Normal ground
Figure 4c. Elevation in Y-direction - Normal ground

Figure 4d. Elevation in X direction - Sloping ground
Figure 4e. Elevation in Y direction - Sloping ground
Seismic analysis results obtained for building models resting on normal and sloping grounds in various seismic zones with and without base isolation are presented in Tables 2 to 5. The dynamic response quantities such as time period, base shear, top floor displacement and inter-storey drift are given in Tables 2, 3, 4 and 5, respectively. For better understanding, the results reported in the above tables are also shown in Figures 5 to 8. The increase in time period of isolated structure with respect to corresponding fixed base structure is given with plus sign within parenthesis in table 2. Likewise, the reduction in base shear, top floor displacement and inter-storey drift of isolated structure with respect to corresponding fixed base structure are given with minus sign within parenthesis in Tables 3, 4 and 5, respectively. In the succeeding sections, the dynamic response quantities such as time period, base shear, top floor displacement and inter-storey drift of isolated structure are compared with respect to corresponding fixed base structure.
It can be seen from results given in Table 2 that the time period of structure depends upon terrain nature, base condition and building height and does not depend upon seismic zone. It can also be seen that the time period of isolated structure of 1 storey to 10 storey height and resting on normal ground is 2.59 to 3.43 times higher than the time period of corresponding fixed base structure. Similarly, the time period of isolated structure of 1 storey to 10 storey height and resting on sloping ground is 2.88 to 3.66 times higher than the time period of corresponding fixed base structure. This shows that the incorporation of isolation system at base level of building increases the time period by about 2.5 to 3.5 times the time period of corresponding fixed base structure depending on terrain condition and height of building. This increase in time period decreases lateral inertia force developed in the building due to earthquake significantly. Furthermore, it can be observed from the results that for a given base condition and height of building, buildings resting on normal ground have higher time period than buildings resting on sloping ground. This shows that buildings resting on sloping ground attract larger force than buildings resting on normal ground. Plot of natural time period versus building height is shown in Figure 5.
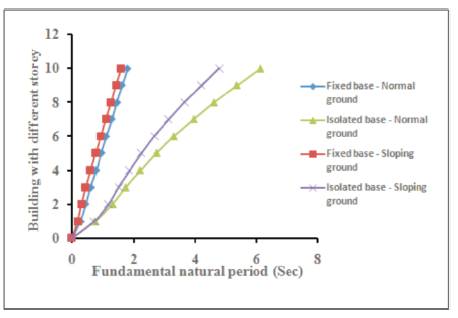
Figure 5. Plot of natural period versus building height
It can be seen from results given in Table 3 that base shear depends upon seismic zone, terrain nature, base condition and building height. It can also be seen that the base shear of isolated structure of 1 storey to 10 storey height and resting on normal ground is only 0.33 to 0.76 times the base shear of corresponding fixed base structure. Similarly, the base shear of isolated structure of 1 storey to 10 storey height and resting on sloping ground is 0.38 to 1.82 times the base shear of corresponding fixed base structure. This indicates that base isolated structure experiences only about one-third of the base shear experienced by corresponding fixed base structure. Furthermore, it can be observed from results that for a given building height with isolated base condition, buildings resting on sloping ground have higher base shear than buildings resting on normal ground. This is obviously due to lower time period for buildings resting on sloping ground. But, in the case of buildings with fixed base condition, the base shear for buildings resting on normal ground upto 4 storey height is higher than buildings resting on sloping ground. However, for buildings beyond 4 storey height, the base shear for buildings resting on normal ground is lower than buildings resting on sloping ground. Plot of building height versus base shear for various zones are shown in Figure 6a to 6d.
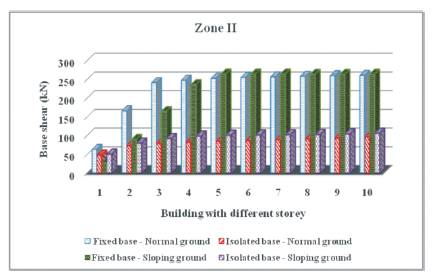
Figure 6a. Plot of building height versus base shear in zone II
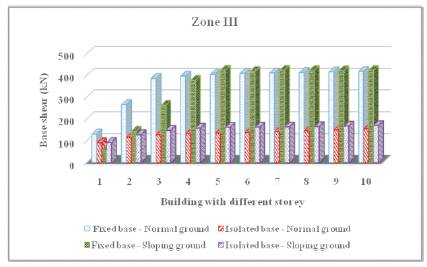
Figure 6b. Plot of building height versus base shear in zone III
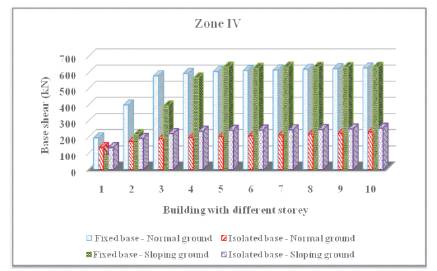
Figure 6c. Plot of building height versus base shear in zone IV
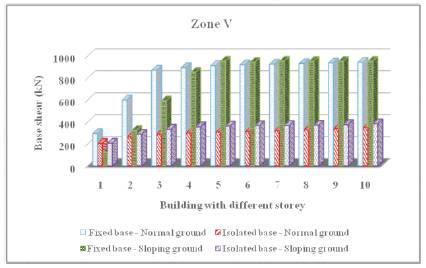
Figure 6d. Plot of building height versus base shear in zone V
It can be seen from results given in Table 4 that top floor displacement, like base shear, depends upon seismic zone, terrain nature, base condition and building height. It can also be seen that the top floor displacement of isolated structure with 1 storey to 10 storey height and resting on normal ground is only 0.03 to 0.05 times the top floor displacement of corresponding fixed base structure. Similarly, the top floor displacement of isolated structure with 1 storey to 10 storey height and resting on sloping ground is 0.00 to 0.10 times the top floor displacement of corresponding fixed base structure. This indicates that base isolated structure experiences about 10% of the top floor displacement experienced by the corresponding fixed base structure and behaves like a rigid structure. Furthermore, it can be observed that for a given base condition and building height, buildings resting on normal ground have higher top floor displacement than buildings resting on sloping ground as shown in Figure 7a to 7d.
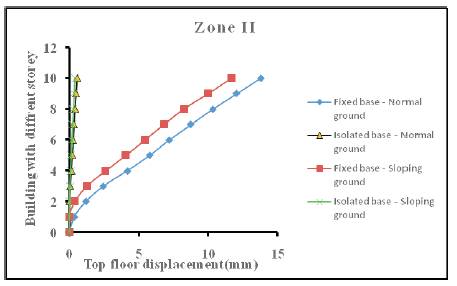
Figure 7a. Plot of top floor displacement versus building height for zone II
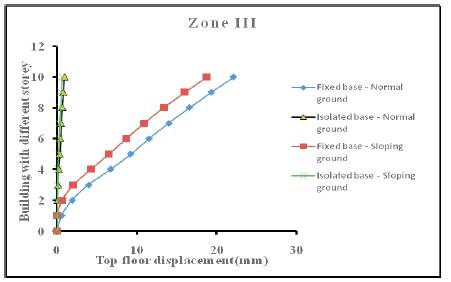
Figure 7b. Plot of top floor displacement versus building height for zone III
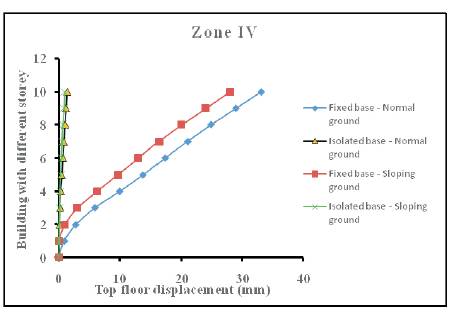
Figure 7c. Plot of top floor displacement versus building height for zone IV

Figure 7d. Plot of top floor displacement versus building height for zone V
It can be seen from results given in table 5 that inter-storey drift, like base shear and top floor displacement, depends upon seismic zone, base condition, terrain nature and building height. It can also be seen that the inter-storey drift of isolated structure with 1 storey to 10 storey height and resting on normal ground is only 0.01 to 0.10 times the interstorey drift of corresponding fixed base structure. Similarly, the inter-storey drift of isolated structure with 1 storey to 10 storey height and resting on sloping ground is 0.02 to 0.07 times the inter-storey drift of corresponding fixed base structure. This is obviously due to rigid body displacement of isolated structure. Furthermore, it can be observed that for a given base condition, terrain nature and building height, the inter-storey drift increases as the seismic zone increases. Plot of inter-storey drift versus storey level for different seismic zones are shown in Figure 8a to 8d.
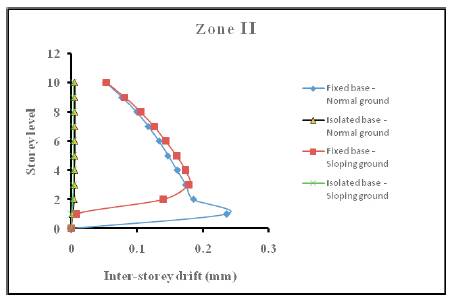
Figure 8a. Plot of inter-storey drift versus storey level for zone II

Figure 8b. Plot of inter-storey drift versus storey level for zone III
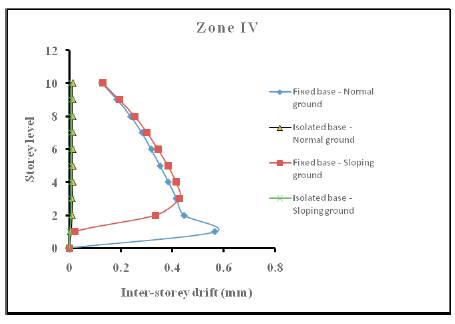
Figure 8c. Plot of inter-storey drift versus storey level for zone IV
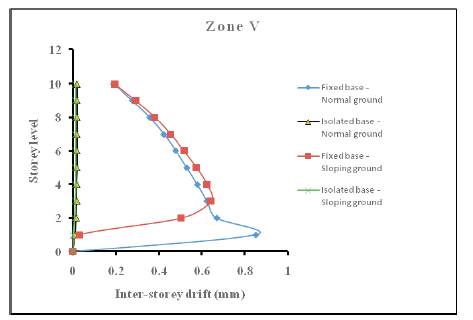
Figure 8d. Plot of inter-storey drift versus storey level for zone V
Based on the seismic analysis carried out in this study, the following conclusions can be drawn: