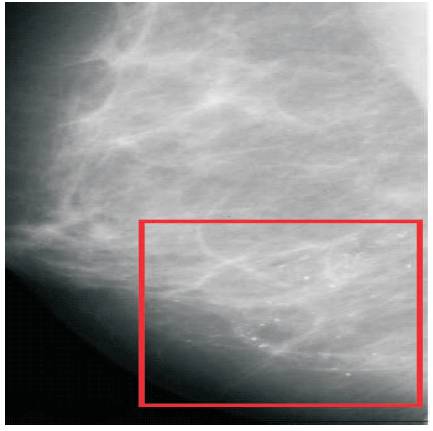
Figure 1. Micro Calcifications
A morphological adaptive bilateral filter based scheme has been proposed for textures segmentation of small field digital mammograms. Mathematical morphology offers flexible operations for extraction of micro calcifications. Unlike the traditional texture filters, adaptive bilateral filter is applied to remove the noise and improve the quality of the selection of the different texture regions. The proposed method uses an adaptive threshold selection, which can remove unwanted textures region from image. The texture regions extract the features of micro calcification and noise boundaries are smoothing again by adaptive bilateral filter. Segmentation results are displayed by inclusion of textures with input image. The proposed method is experimented on 10 micro calcification images and the quality of the method is evaluated.
Mammogram image analysis is used to detect cancer in the breast of suspicious women. It can produce in-depth structures of breast tissues. In order to identify these structures, the radiological studies have chosen only mammograms than other modalities images [1-3]. The small tissue structures in the mammograms also known as micro calcifications [4-6] are shown in Figure 1. Micro calcifications has to be detected and the shape has to be analyzed, which further allows to identify whether the lesions are either benign or malignant [21]. These deposits consist of calcium at thickness of small tissues and are symbolized as little white dots. These clearly give the initial signs of cancer. Some of the micro calcifications that are malignant appear in sizes of less than 2mm, while others appear as cluster, also called benign and the size is more than 2mm. Malignant are grouped in near distance [8] .

Figure 1. Micro Calcifications
The malignant are normally heterogeneous in structure and irregular in shape, whereas benign is of homogenous structure and appears clearly in centre. Radiologists also considered age of lesions time over certain period. If the size of the calcifications varies continuously after regular checkups of woman, it can be suspected as malignant, otherwise if its constant in size, it is considered as benign. It is noted that segmental distribution is not random. This can be checked through analytic biopsy.
Texture of gray level image is the Intensity variation on surface, quantifying properties such as regularity, smoothness and roughness. Texture is mapping on surface of the image using mathematical techniques which may be called as surface texture. There are three approaches used to explain the texture. Those are structural, spectral and statistical approaches. The level of gray value is a parameter to differentiate the visual homogeneity of given region of an image from a true image to generate another image based on the texture and analyze the two areas by separating them or form the same texture. In order to compare the texture samples to decide the zones, Texture segmentation involves precisely screening an image into different types of textured regions. It needs concurrent measurements in both the spatial and the spatial-frequency domains. Gabor filters are well accepted in the present days as a joint spatial/spatial-frequency representation of textures. Daugman [16] has shown that Gabor filters are implemented successfully on localization techniques using both spatial and spatial-frequency domain. In addition, they are band pass filters.
Liu, S [5] Rashed et.al [6], Qianet.al [7] Chen cet.al [8] wang T et.al [9] concentrated on multiscale features on mammograms. The method extracted the texture information of Energy, entropy and homogeneity using discrete transforms. Kim J.K et.al [10] applied statistical texture features on mammograms and extracted the lesions. The proposed method is developed on statistically based methods like GLCM (Gray Level Co occurrence Matrix) and Spatially Gray Level Dependence matrix (SGLD). The process of the method is to consider parameters like energy measure, Correlation, Inertia, Entropy, variance and standard deviation. Lefebvre f et.al (1992) generated the cancer detection by fractal feature measurement. The method developed textures of rough and smooth areas using fractal dimension. The study [12] applied a model based vision of DOG (difference of Gaussian) filters to detect the masses in mammograms. The method successfully extracted nine features from mammogram images. The study also applied mathematical morphological operators to extract micro calcifications from mammograms. The method marked a suspicious area and extracted morphological features such as shape etc.
Buyue Zhang et.al [15] proposed an Adaptive Bilateral Filter (ABF), which showed a good performance than the ordinary bilateral filters. But it has two important changes. One, an offset value is included along with range filter. Next, both width and range of the adaptive filters are varied with respect to output value. Laplacian of Gaussian (LOG) operation on the output improved the sharpness of edges. It is purely dependent on the image structure. They are able to minimize the MSE between the original and reconstructed images for each class of pixels.
Alexander Wong [16] introduced a different perceptually based process for noise removal of image signals represented by low signal to noise ratios. Results have shown that the process is effective in removing signal noise, while enhancing both qualitatively and quantitatively. Jinshan Tang et.al [17] developed a new bilateral filter method to reduce speckle noise reduction in ultrasound images for the purpose of segmentation and Measurement. H.W. Kang et.al [18] introduced an adaptive bilateral filter to adaptively preserve the curve strokes and reduce superimposed noise on the image. This method made easy the automatic generation of artistic illustration in order to adaptively guide the curved stroke directions based on the importance of map. The experimental results have shown that the scheme facilitates automatic production of artistic illustrations in a broad range of styles.
Mathematical morphology is one of the popular emerging areas in image processing consisting of a simple set of technical operations called dilation, erosion and remaining operations are a combination of these two [19]. Yoshinori ITO [21] proposed an impulse noise removal filter using mathematical morphology. Xiaoping Linet.al [19] attempted Mathematical Morphology techniques in the process of feature extraction using SCILAB toolbox which is an openly used software having connection to mathematical morphology tool box.
Joseph M. Reinhard et.al [20] described an adaptable search-based approach for morphological Shape enhancement. The studies proposed a fourth order diffusion Partial Differential Equations (PDE) and a smoothing technique to reduce processing time and improve the performance of this model. B.Sridhar et.al [2] presented the performance analysis of adaptive bilateral filter to evaluate the pixel to noise ratio and mean square errors by changing parameters of the adaptive filter is half width values and standard deviations.
The proposed method is meant to extract micro calcifications by considering the texture features. Combinational mathematical morphological operations erosion and dilations are applied on the mammogram to extract the suspicious area features such as shape and sizes. To efficiently separate the rough surface and smooth area, an adaptive thresholding technique is included.
The paper is organized as follows in Section 1, the background required to effectively implement the algorithm is presented. The proposed algorithm is described in Section 2. After that, application of the proposed algorithm and discussion is described in section 4, and conclusions are drawn in section 5.
The most basic morphological operations are dilation and erosion. Dilation adds pixels to the boundaries of objects in an image, while erosion removes pixels on object boundaries. The number of pixels added or removed from the objects in an image depends on the size and shape of the structuring element used to process the image. In the morphological dilation and erosion operations, the state of any given pixel in the output image is determined by applying a rule to the corresponding pixel and its neighbors in the input image. The rule used to process the pixels defines the operation as dilation or erosion [11].
An essential part of the dilation and erosion operations is the structuring element used to probe the input image. Structuring element is a matrix consisting of only 0's and 1's that can have any arbitrary shape and size [19]. The pixels with values of 1 define the neighborhood. Twodimensional, or flat structuring elements are typically much smaller than the image being processed. The center pixel of the structuring element, called the origin, identifies the pixel of interest or the pixel being processed. The pixels in the structuring element containing 1s define the neighborhood of the structuring element. These pixels are also considered in dilation or erosion processing.
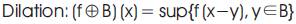
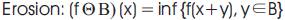
These names can be easily motivated when considering a shape in a binary image and a disc shaped structuring element. In this case, dilation blows up its boundaries, while erosion shrinks them. Dilation and erosion form the basis for constructing other morphological processes, for instance opening and closing.
The two basic morphological operations, dilation and erosion with a structuring element B, are defined for a grey-scale image f ∈L α (Ir2) by [1]
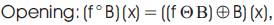
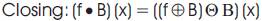
In the preceding shape interpretation, opening smoothes the shape by breaking narrow eliminating small islands, while closing smoothes by eliminating small holes.
These are classified into Omni directional and multi scaled elements, which is one way to plot out square windows [18]. In general, consider α is the angle of rotation. Let us consider N is a value, then order of the SE is (2N+1) X (2N+1). Then the equation of the structure element is represented as
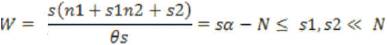
For all s=0, 1 --- 4N-1 and α is the angle of the rotation expressed as α =1800/4N.Suppose N=2, then dimension of the SE is 5 x5, the angle value is obtained as α=0, 22.5, 45,135,157.5.
Consider structure element sequence having same shape in common and size is increased following the accretion of i, then defining to different features from the various values of image, the size of the structure must be adjusted. In general, a basic structure element shape is selected and the number of structure elements is of the order of (2i+1) X (2i+1).
Bilateral filtering smoothens images while preserving edges, by means of a nonlinear combination of nearby image values. The method is non-iterative, local, and simple. It combines gray levels or colors based on geometric closeness and photometric similarity, and prefers near values to distant values in both domain and range. The bilateral filter proposed by Tomasi and Manduchi in 1998 is a nonlinear filter that smoothes the noise while preserving edge structures [15]. Bilateral filter is a spatial domain filter, the response of the filter is given in equation 6,
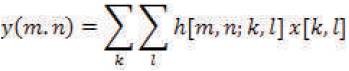
Y(m,n) is the noise removed image.
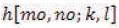 is the response at
[m,n] to an impulse I[k, l]
and x [m,n] is the degraded image.
is the response at
[m,n] to an impulse I[k, l]
and x [m,n] is the degraded image.
Where 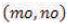 is the center pixel
of the window
is the center pixel
of the window 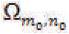
σd and σr are the standard deviations of the domain and range Gaussian filters, respectively

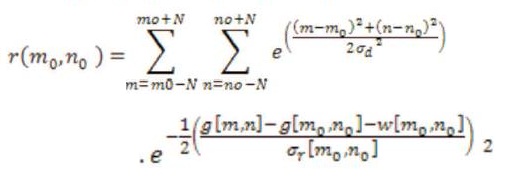

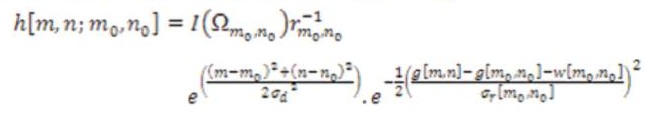
r(mo,no) is a normalization factor that assures that the filter preserves average gray value in constant areas of the image.
A Gaussian filter filters the low frequency noise and restores the edges. Combinations of domain and range Gaussian filters are applied here to give maximum weight pixels near the centre value. Combined operations of domain and range filters along with the bilateral filter at nearer to edge pixel gray level values is becoming highlighted out and Gaussian filter is slopping around the edge. This guarantee takes an average of adjacent pixel values and minimizes the gradient direction. Thus, the bilateral filter greatly smoothen the noise and restore the edge formations.
The ABF maintains the actual form of bilateral filter [16]. In addition two significant modifications are included. Equations 7 & 8 consists of two exponential functions, one is the operator of range filters and second the domain filter functions. The range filters included an offset (w) function and width is introduced in domain filters. If the offset value is zero and width is constant the ABF acts as an ordinary bilateral filter. The variation of these two values or either one is fixed, and the filters show effective performance to restore the image and sharpen the edges. It is concentrated on edges at maximum level and improves the slope.
In ABF, the pixel gray level variation plays an important role during the training of filter [20]. Here we have chosen difference between centre pixel value and mean of the local widow. Its response gives more effects on the strength of edges, separates the regions and reduces the robustness to the noise. Laplacian of Gaussian(LOG) is applied to the image before filtering process is undergone.
The proposed method is shown in Figure 2 as the block diagram of a Texture segmentation process. Here two Adaptive Bilateral Filters (ABF) are applied to separate a texture. Micro calcifications are considered here as textures. Mathematical morphological operators are acting as a crucial role in separating top and bottom level textures.
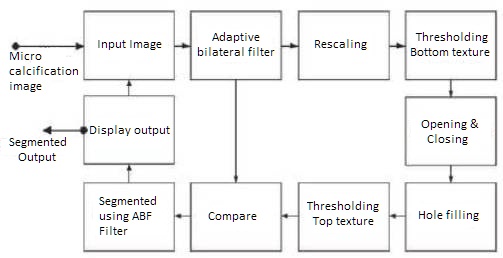
Figure 2. Block diagram of the proposed method
As shown in block diagram an input small field's breast mammogram is chosen. Most of the medical images are represented in gray level form. The mammogram consists most of the noises at low frequency level, also edges are important to detect the malignancy in the image. To improve the quality and isolate the regions of an image, ABF filters is used. This smoothes the image and preserves texture regions. It can separate the energy levels in the image [16]. The energy distribution exhibits the statistically random nature on the image. Rescaling the image into a square dimension gives an effective segmentation of textures. Apply the threshold on the image to separately identify top and bottom structures based on intensity level or gray level [2]. A threshold value is randomly selected for texture separations, which is dependent on the width and offset values used in ABF.
Image is converted from gray to binary and both images are compared to identify that top texture is over segmented and bottom is almost segmented. To extract the bottom an opening technique along with flat structure element of dimensions 9 x 9 is applied. Finally edges are smoothed by means of closing operation with structure element of same dimension(9) [15]. In case of generation of unidentified gaps, morphological operator hole filling is used [22]. Actually a mask (structure element) segments the top texture where as bottom one need not be concentrated, also bottom texture is not properly segmented by this operation. Once again compare the input to the binary image using a mask operator of dimension 9 x 9 [18]. This operation is helpful to relocate texture on the original image. Here a repetitive care must be taken to check the dimension of images. If the dimension is not same, adjust dimensions of the texture image. To remove the unwanted regions and smoothen the image and sharpen the edges once again ABF filter is applied on image. We require the top texture use once again, for opening operations and these results are super imposed to get segmented result. That is, micro calcifications are highlighted and the results of the simulated algorithm are shown in Figure 3. The input image of small field micro calcification is shown in Figure 3(a). Extracted rough bottom texture is highlighted in Figure 3(b). This result is generated after thresholding. Again apply the top thresholding along with morphological operators and the result of the image is given in 3 ( C). The top texture and input image is compared and the results give the extraction of micro calcifications as shown in Figure 3(d). The highlighted regions of micro calcifications are shown in Figure 3(e).

Figure 3. Results of applying proposed method a) micro calcification mammogram b) Extracted rough bottom texture c) Extracted top raw texture d)Segmented micro calcifications. e) Highlighting the micro calcifications with edges.
Similarly the same kind of process is experimented with 10 micro calcification on different images of mammogram. This experiment was done with help of radiologists, initially the radiologists marked doubtful areas consisting of cancer on mammogram. Those are separated digitally and given input to the proposed system. Another example is also presented in Figure 4 with appropriate threshold value. Figure 4(a) shows the input image. Figure 4(b) is the segmentation of micro calcifications. Figure 4(c) is the highlighted micro calcifications on the mammo grams.

Figure 4. Results of applying proposed method a) input micro calcification mammogram b) Segmented micro calcifications. c) Highlighting the micro calcifications with edges.
Main advantage of the method is maximum accuracy is provided when the edge of the region is properly sharpened. Otherwise segmentation process comes to a low level that can be observed as shown in Figure 4( c).
The algorithm is experimented on nearly 10 small field mammograms having micro calcifications that can lead to cancer selected by two radiologists. Out of these, two micro calcification results are shown in Figures 3 & 4. To evaluate, the texture segment algorithm identified a metric named Pratt's quality measurement [24]. It is especially used to compare the systems which do not work on the same segmentation applications. Here the computer simulation results obtained by the method are compared with radiologist's evaluation of micro calcifications. Pratt's measurement metric (FOM) is expressed as,
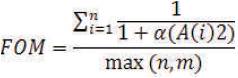
Let 'n' be the number of micro calcification detected by the computer aided method and 'm' be the number of micro calcifications detected by the radiologists. A (i) is the distance obtained between centre pixels detected by computer and radiologists. Radiologist identified lesions are using ordinary small field mammogram. To measure the parameters, experienced radiologist detection is chosen a reference value. Where α is the scaling constant given by the evaluator. In this calculation, are consider the value of α as 0.05. The results are calculated and depicted in Figure 5, the graph is drawn between the FOM on y axis where images numbered from 1 to 10 are given on x-axis in order. The value of the FOM is obtained in between the range [0, 1]. If the proposed method is extract identified and the boundary and centre pixel is matched, the FOM is 1, otherwise it varies in between 0 to 1. In this measurement process, the ground truth data were collected [23] and included for comparison. Here chosen radiologist-1 has less experience while radiologist-2 is with good experience in detection of cancer using mammograms. Figure 5 shows the proposed method’s performance existing between that of radiologist-1 and radiologist 2. The average number of FOMs are calculated as 0.56, 0.68, and 0.66 for radiologist-1, radiologist-2 and proposed method respectively.
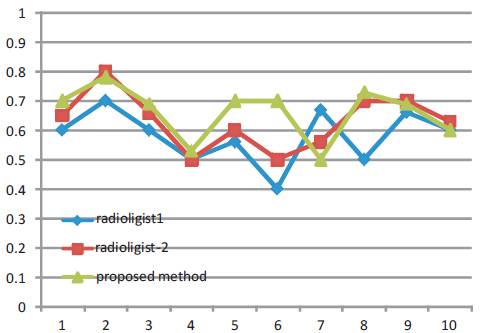
Figure 5. FOM Vs number of the image
The authors have presented a new texture segmentation method based on adaptive bilateral method. Mathematical morphology is applied on micro calcifications image and it successfully detected the lesions. This method increased the true positives of the image lesions being identified and classified as benign and malignant. Proposed method generated results with 95% and reduced the false positives up to 2.5 per image. The proposed method evaluated with metric Pratt's measurement, which is compared with the radiologist. The experimental results show that the results obtained by this method are compared with human segmentation. Hence, this method can be preferred for diagnosis of early detection malignancy as second reader option in mammogram image analysis. This method sometimes gives more number of false positives, if low quality digital mammogram is chosen. In future work, the micro calcifications accuracy will be improved by representing segmented images in three dimensions, and the evaluation process also needs to be improved by using artificial neural network methods.
This research work is fully funded and supported by authors’ Institutions. The authors show their gratitude to the Institutions, Head of the Institutions, Co Faculty and Scholars. The authors are thankful to the Local government Hospital for their support and clinical suggestions to progress this work.