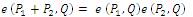
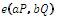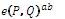= 
for all P1, Q ∈ G1 and a, b ∈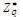 
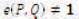if 
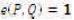for all Q∈ E[n] then P=O and also that if 
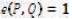for all Q ∈ E[n] then P = O.
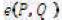for all P, Q ∈ G1 .The security of email can be considered one of the important issues for scientific research since the nineties of the last century. This is mainly comes from the wide use of e-mail for exchanging various kinds of information especially that some of them are important or sensitive. Although there have been several solutions offered to solve this problem but we still facing the fact that most email messages sent so far have been without any security. The main reason behind this is that, the previous systems relied on the traditional public key cryptography were so complicated from usability point of view for most users.
In this work, the authors exploit the use of Identity-Based Cryptography (IBC) for solving this usability problem. Indeed, to further increase the system strength, IBC has been combined with mediated RSA cryptography. The proposal includes the deployment of the two promising hybrids of mediated IBC. In both of these hybrid cryptographic systems, all operations of encryption/decryption and signature/verification have been considered. The proposed system has met the design objectives either totally or partially. They believe that the proposed hybrids for mediated IBC can be very helpful in simplifing the use of e-mail security so that to increase the number of users of such systems.
Most of available secure e-mailing systems rely on Public Key Cryptography (PKC) for key management and signature issues. However, most people continuously fail in protecting themselves, despite the long time that has passed on the availability of systems that based on public-key infrastructure (PKI). The main reason for this is that PKI is just too difficult for the average user. A wellknown difficulty with the use of public key cryptographic systems is the verification and distribution of the public keys. Therefore; it requires a tremendous overhead in terms of setting up a public key. A relatively new trend of research in this direction is to use Identity-Based Cryptography (IBC) in securing e-mail systems so that to make them easier for use by users. IBC facilitates easy introduction of PKC by allowing an entity's public key to be derived from an arbitrary identification value, such as email address. Thus, it greatly reduces the need for public key certificates. However, IBC techniques are not compatible with popular public key encr yption algorithms. On the other hand, mediated cryptography or mediated RSA (mRSA) achieves simple splitting of RSA private key between the user and a Security Mediator allowing fine-grained control of users' security privileges. However, mediate cryptography relies on public key certificates to manage public keys.
In this paper, the authors present an interesting two hybrid techniques of IBC and mediated cryptography for securing e-mail systems. The first one combines between Boneh-Franklin Identity-based Encryption (BF-IBE) and Sakai-Ogishi-Kasahara Identity-Based Signature (SOK-IBS) with mediated cryptography. The second proposal depends on the Boneh-Boyen IBE (BB-IBE). Since to the best of authors' knowledge, there is no IBS scheme that corresponds to BB-IBE in the way of private key generation, we suggest a new signature scheme compatible with BBIBE that we call Compatible Signature Algorithm IBS (CSAIBS). We have called this second cryptographic hybrid system proposal as the "Mediated BB-CSA IBC" Scheme. In addition, a secure e-mail system based on both of these hybrid security techniques has been developed and tested.
The remaining of this paper is organized as follows: Section 1 contains some necessary cryptographic background including mRSA and IBC. Then, a general description of the proposed system architecture is presented in Section 2. The first proposed hybrid mediated IBC security technique that we call the "Mediated BF-SOK IBC" Scheme is described in Section 3, while the second proposed hybrid cryptographic technique called the "Mediated BB-CSA IBC" Scheme is described in Section 4 along with some security analysis. Next, Section 5 outlines the operation of the system. Finally, the paper is concluded.
PKC requires the receiver's public key. As a consequence, before sending any message, the sender should obtain this public key. Moreover, he should make sure that the public key he obtains is indeed the correct one. This introduces two important steps in real life implementation, fetching the public key and verifying it. The traditional solution that allows one to verify a public key is public-key certificates. At the most basic level, a public-key certificate is simply a message that asserts: “The public key of user Bob is upk ”. To make sure that the B certificate is genuine, it needs to be signed (Martin, 2008). To use a public key that is contained in a digital certificate, a user queries the public repository where the certificate can be found and retrieves the certificate. Because a public key may be valid for quite a while, it is often necessary to check such a public key for validity before using it. A much more difficult problem when using such certificates is the management of trust. This is related to what guarantee can be given to trust the owner of the verification key. The PKI provides the digital certificates that can identify the individual's identity. PKI is a combination of hardware, software, encr yption technology, people, and policies (Kuhn, Hu, Polk, & Chang, 2001; Vacca, 2004).
Security-mediated cryptography is an approach for fast certification revocation centered about the concept of an on-line semi-trusted mediator (SEM) (Boneh, Ding, Tsudik, & Wong, 2001). It is used to help the client in completing sign and decrypt message where the client must first obtain message-specific token from SEM. Without this token the client cannot use his/her private key. The security mediated approach has many advantages such that, the full operation cannot accomplish without acceptance of SEM. Thus, it reduces or eliminates need to certification revocation The SEM uses to immediate revocation of user's ability to sign or decrypt the message. The SEM itself cannot gain any useful information because it is only able partially to decrypt or sign the message. The main idea behind mRSA is the splitting of an RSA private key into two parts as in threshold RSA, one of the two is given to user and other given to SEM, no one can use knowledge half-key (its own part) to derive another half (Boneh, Ding, Tsudik, & Wong, 2001; Koga, Imamoto, & Sakurai, 2005).
Around the mid 1980's, the concept of IBC was introduced. IBC can offer a nice solution to some important practical security problems. This concept is used to eliminate the complexity of using digital certificates. In IBC, the public key of a user can be derived from public information that uniquely identifies the user. It allows a party to encrypt a message using the recipient's identity as a public key. The corresponding private key is generated by a trusted third party called the Private Key Generator (PKG). ID based cr yptosystems are advantageous over the traditional public key cryptosystems as they avoid the need of certified public key register (Guan, Cao, Zhao, Chen, Chen, & Nan, 2008; Martin, 2008). In 2001, Boneh and Franklin gave a practical Identity-Based Encryption scheme that relies on the bilinear Diffie-Hellman problem for its security. It uses a complicated mathematical transformation called the Tate pairing (Boneh & Franklin, 1985; Martin, 2005).
This can be described as follows: Let G1 be a cyclic group generated by P1, whose order is a prime q, and G2 be a cyclic multiplicative group of the same order. The discrete logarithm problems in both G1 and G2 are hard. Then e: G1 × G1 → G2 is a pairing which satisfies the following properties (Agarwal, Shrimali, & Das, 2009; Yong, Yang, & Son, 2007):
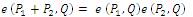
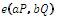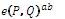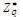
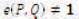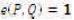= for all P1, Q ∈ G1 and a, b ∈ if for all Q∈ E[n] then P=O and also that if 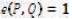for all Q ∈ E[n] then P = O. 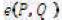for all P, Q ∈ G1 .There are some computational problems which have the property that they are of suitable hardness to be used to create public-key algorithms. Some of such relevant computational problems which depend on Diffie- Hellman problem are: the Decision Diffie-Hellman Problem (DDHP), the Bilinear Diffie-Hellman Problem (BDHP), and the Decision Bilinear Diffie-Hellman Problem (DBDHP). The DDHP is a computational hardness assumption about a certain problem involving discrete logarithms in cyclic groups. The BDHP is a generalization of the DHP to groups with a pairing. Finally, the DBDHP generalizes the DDHP (Galbraith, 2011; Abdalla, Kiltz, & Neven, 2008).
Another important technique is the Fujisaki-Okamoto Transform which was invented by Fujisaki and Okamoto in 1999. This transform is widely known to be able to generically transform a public-key encryption algorithm with fairly weak properties into one which is secure against chosen cipher-text attacks. Thus, this transformation can be used to create a more secure scheme from a less secure algorithm (Fujiski & Okamoto, 1999; Yang, Kitagawa, Hanaoka, Zhang, Matsuura, & Imai, 2006).
In general, an IBC protocol can be defined formally as a family of algorithms, usually consisting of four algorithms. An Identity-Based Encryption (IBE) scheme consists of: Setup, Private key Extraction (Generation), Encryption, and Decryption. While an Identity-Based Signature (IBS) scheme can be described by replacing the Encryption and Decryption steps with Sign and Verify algorithms (Joye & Neven, 2009).
The main design goals of the proposed email security system are as follows:
Two methods have been used to provide the security, which are: IBC and mediated cryptography. Each one of them is composed of parts that work together to achieve the aims. By combining IBC and mediated cryptography, the resultant system will consist of three parts. The first part is used for generating private keys from public information (public key) and public parameters and it is called the Generation Center (GC). It has three functions: generating public parameters (Parameters Generation Center or PGC), generating the private key from a public key which be often email address (Private Key Generation Center or PKGC), and dividing the private key into two parts and giving one for user and other for the SEM. The GC is considered the trusted authority where it knows all keys of users. Hence, any compromise of it will expose the system to destruction. The second part is SEM which completes decrypting/signing for user and it has the half of the user's private key. SEM takes all the halves of the users' private keys from PKGC and stores them in the database. The client is the third part of the designed system, which should download the parameters before requesting his private key from PKGC in order to use the system. Figure 1 illustrates the general structure of the system, which mainly represents an email client capable of secure messaging.
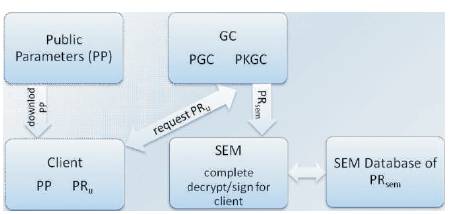
Figure 1. General Structure of the Proposed System
Delivering private key to user should be performed secretly. Keys distribution protocols are necessary to establish a secure channel, where there is a need to session key (secret key) to achieve that. This secret key is transferred with the use of PKGC's public key. The authentication process is accomplished by using the message digest algorithm. The user must send his/her email address as definition of identifies, this method does not guarantee the credibility, but guarantee the response will be send to this address. This method prevents the forgers from benefit impersonation of another user because they cannot arrive to email contents. The user should obtain the email address of PKGC to send the request. This process executes between user and PKGC, as described by the following steps (Figure 2):
Figure 2. Private Key Distribution
Step1: The user (email client) must first obtain the public system parameters to be able to generate the cipher-text of message request by IBE.
Step2: The user generates the session key which is used by a PKGC. Then the email client creates request that includes: user's email address, timestamp, session key and message digest of (email address, time stamp and session key). The message digest is added to detect any change in request (integrity). This request is encrypted with public key of PKGC by using IBE (PKGC's public key is the email address). The request is then sent.
Step3: The PKGC receives the request message, it decrypts the request to extract session key, and computes the message digest for request to compare with message digest which was sent. If true, then the PKGC generates the user's private key depending on the email address that is appended in the message as corresponding public key. The PKGC constructs the responding message and encrypts it using the session key by using any symmetric algorithm (the AES is used in our implementation), and signs it by using PKGC's private key. After that it sends the result to user by using the email address.
Step 4: After receiving the message from PKGC, the user decrypts it by the same session key to retrieve the private key. Then the user verifies the sign using the public key.
In order to use IBC for securing email, we must enable both signature and encryption. However, the problem is that not all IBC schemes use the same method to generate the private key. This means that the private key almost in any scheme is not similar to that generated by other scheme. Consequently, the user needs two private keys, one for encryption and other for signature. For this reason, the schemes must be chosen carefully to be compatible with each other to have the same algorithms (setup, extract) which are used in GC. These hybrid techniques which combine between IBE, IBS, and mediated cryptography can be the best choice to solve the problem of usability in secure email.
In this work, the authors have developed and applied two promising hybrid cryptographic techniques for this purpose. The first one combines between Boneh-Franklin Identity-based Encryption (BF-IBE) and Sakai-Ogishi- Kasahara Identity-Based Signature (SOK-IBS) with mediated cryptography. This proposal is described in this section. The second proposal depends on the Boneh- Boyen IBE (BB-IBE) scheme and it will be described in the next section.
Considering the first proposal, which we call the “Mediated BF-SOK IBC" Scheme, the BF-IBE scheme cannot be used for signature service; therefore, the SOKIBS scheme is used to do this service. Both schemes depend on identity information as public key and both have similar algorithms for setup and extract. The required modification will be applied on extraction of the private key to be split into two parts. In signature algorithms, the sign algorithm will also be shared between user and SEM. This means that it will perform in two steps. Although the verification algorithm is required only by the recipient, it must be modified to be compatible with modified signature algorithm. Since the need to the private key will be only in decryption, the change in BF scheme will be only on the decryption algorithm without modifying on encryption algorithm.
This scheme consists of three parties: GC, SEM, and users. It also contains four algorithms: Setup, Extract, Encrypt and Decrypt. The GC governs the SEM and a SEM can serve many users. Two of the algorithms, Setup and Encrypt, are analogous to those in the original BF scheme. The others, Extract and Decrypt, provide the mediated cryptography capability. These four algorithms are described as follows:
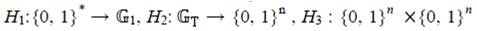
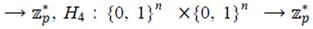
1. Calculate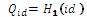 
2.Pick a random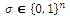 
3.Calculate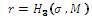 
4. Calculate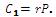
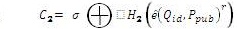
5.Calculate
| 6.Calculate The Ciphertext is C=(C1,C2,C3) | (3) |
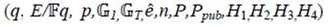
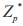computes Qid = H2 (id), Duser = su Qid and Dsem = (s – su )Qid . Duser is sent secretly to the user whose identity is ID as his private key and (Dsem , id) is sent to the SEM.User:
1. Pick a random number x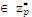 
2. Calculate D1 =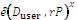 
3. Calculate D2 =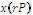
The user sends (D1 , D2 ) to SEM
SEM:
1. Calculate D3 = D1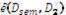
2. Return D3 to user
User:
3. Calculate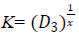 
4. Calculate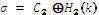 
5. Calculate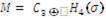 
6. Calculate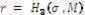 
Calculate rP. If C1 ≠ rP then reject the ciphertext as invalid.
This scheme is based on the SOK-IBS scheme. It also consists of three parties: GC, SEM, and users. In addition, it has four algorithms: Setup, Extract, Sign and Verify. Two of the algorithms, Setup and Extract, are analogous to those in Mediated BF-IBE scheme. The others, Verify and Sign, are different which provide the mediated signature's capability. They are described as follows:
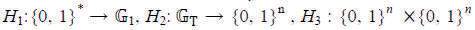
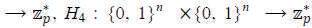, The master secret is s and the public parameters are the similar use in BF Full schema,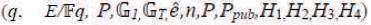 
User:
1. Calculate SHA =H(M)
2. Choose random number u and Calculate U1 =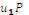 
3. The user sends (U1 , SHA, id) to SEM.
SEM
1. Calculate H = H1 (SHA)
2. Choose random number u2 and Calculate U2 =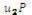 
3. Calculate U= U1 + U2
4. Calculate h =H2 (SHA, U, id)
5. Calculate Ssem = hDsem + u2 (Ppub + H)
6. Return (U, Ssem ) to user
User
1. Calculate H = H1 (SHA)
2. Calculate h =H3 (SHA, U, id)
3. Calculate Suser = hDuser + u1 (Ppub +H)
4. Calculate S=Ssem+Suser
| The Signature is σ=(U,S) | (4) |
1. Calculates SHA =H(M)
2. Calculates H = H1 (SHA)
3. Calculates Qid = H1 (id)
4. Calculates h =H3 (SHA, U, id)
If,  |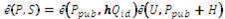
(5) |
then he/she accepts the signature.
In the second proposal, the BB-IBE scheme is modified to create a hybrid mediated system. The BB-IBE cannot be used as a signature scheme. Thus, we need another scheme to do this job. However, to the best of our knowledge, there exists no signature scheme that corresponds to BB-IBE in the way of private key generation. Hence, in this second proposal, the authors suggest a new signature scheme compatible with BB-IBE that we called Compatible Signature Algorithm IBS (CSA-IBS). Both schemes are based on identity information as the public key, and both have similar algorithm for setup and extract. The modification will mainly be done on the extraction of the private key to split it into two parts. Indeed, in BB-IBE the change will also apply on the decryption algorithm along with a simple modification on encryption algorithm. This is required to enable achieving the decryption of ciphertext in cooperation between SEM and user. The CSA-IBS Algorithm has been fully built to be compatible with BB-IBE in order to get the same private key which will be used in decryption and signature. Of course, the Sign algorithm will be performed through cooperation between user and SEM. This second cryptographic hybrid system proposal we call the "Mediated BB-CSA IBC" Scheme.
As in the previous proposed scheme, this scheme also consists of three parties: GC, SEM and users. Indeed, it includes four algorithms: Setup, Extract, Encrypt and Decrypt. The Setup algorithm is analogous to that in original scheme, and the others, Extract, Encryption, and Decryption algorithms have been modified to provide the mediated cryptography capability. They can be described as follows:
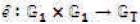. To do this we pick an elliptic curve E/F q with embedding degree k, and a prime p such that p|#E(Fq). Then Choose an arbitrary generator P ∈ G, pick a random Three integers α, β, γ ∈Zp and set P1 = αP, P2 = βP, P3 = γP, and also a constant 
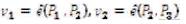and chosen cryptographic hash functions (H1 , H2 , H3 ). The public parameters are the similar use in BB Full schema are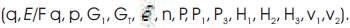 
1. Compute qid= H1 (id),
2. Compute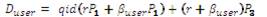 
and
3. Compute βsem=β-βuser
4. Compute Dsem=(βsem-r)P
Duser is sent secretly to the user whose identity is id as his user private key and (Dsem , id) is sent to the SEM.
1. Calculate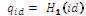 
2. Pick random
3. Calculate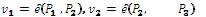
4. Calculate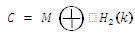
<>/p
5. Calculate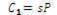
6. Calculate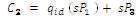
7. Calculate
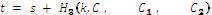
Then, the cipher-text is  |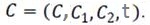
(6) |
User
1. Pick a random number x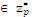 
2. Calculate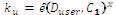 
3. Calculate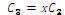
4. The user sends (k1 , C3 , id) to SEM.
SEM:
1. Calculate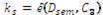 
2. Calculate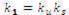 
3. Return (k1 ) to user
User:
1) Calculate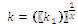
2) Calculate
3) Verify that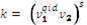 
and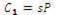
. If either condition fails, raise an error condition and exit.
This is our own developed technique for achieving the concept of mediated IBS that can be efficiently mixed with the Mediated BB-IBE to give a concrete security scheme. The private key generation algorithm in this scheme is similar to that in the Mediated BB-IBE. This scheme has higher efficiency comparable to others IBS schemes. The scheme consists of four algorithms:
1. Compute qid= H1 (id),
2. Compute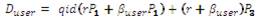 
and
3. Compute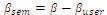 
4. Compute
The Duser send secretly to the user whose identity is id as his user private key and (Dsem ,id) is sent to the SEM.
User
1. Calculate SHA =H(M)
2. Choose random number u and Calculates U1 =Su P
3. The user sends (U1 , SHA, id) to SEM.
SEM
1. Calculate H = H1 (SHA)
2. Calculate qid= H1 (id),
3. Choose random number u2 and Calculates U2 =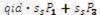 
4. Calculate U= U1 + U2 .
5. Calculate Ssem = Dsem +Ss H.
6. Return (U, Ssem ) to user
User
1. Calculates H =H1(SHA)
To do this pick an elliptic curve E/F q with embedding degree k, and a prime number p where p|#E(F q). Then Choose an arbitrary generator P ∈ G, pick a random Three integers α, β, γ ∈ Zp and set P1 =α P, P2 = βP, P3 = γP, and also a constant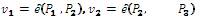 
and chosen cryptographic hash functions (H1 , H2 , H3 ). The public parameters are the similar use in BB Full schema are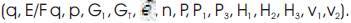 
Calculates Suser = Duser + Su H
The Signature is  |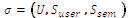
(7) |
1. Calculates SHA =H(M)
2. Calculates H = H1 (SHA)
3. Calculates qid= H1 (id)
4. Calculates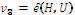 
5. Calculates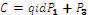 
6. If 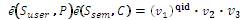 then he accepts the signature. |
(8) |
Despite that fact that we have done a through correctness and security analysis for all components of the two proposed mediated IBC hybrid systems; however, for reasons of space limitation we will only include some analysis for the Mediated CSA-IBS scheme in this paper. The security analysis for all cryptographic components and schemes in our two proposals can be the issue for a subsequent paper.
The correctness of signature obtained from this scheme can be proved according to the following steps:
If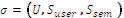 
is a valid signature on M under ID, then:
 |
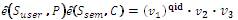(9) |
where:
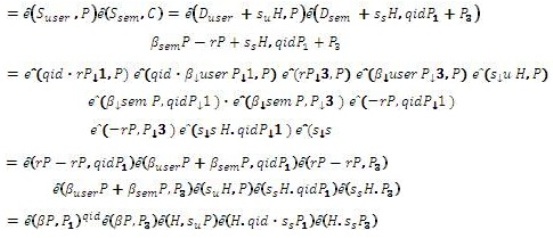
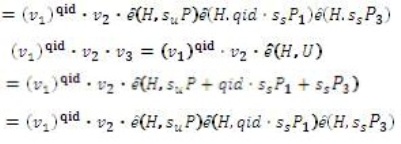
The signature issuing algorithm of this scheme has the more complexity compare to the Mediated SOK-IBS scheme. However, the verification algorithms in both systems have the same cost because they require three pairing computations. The security of this scheme is increase because the key is more complex from the Mediated SOK-IBS. Here, the attacker to forge the signature, he must obtain (by men-in-the-middle-attack) the two random numbers (Su and Ss ) so as to be able to replace the original message with his message. This means he/she should calculate Su from SuP by calculating a discrete logarithm sP and calculate S from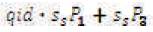 
by S calculating a discrete logarithm sP1 or sP3 . However, this is not a simple operation because he/she must separate 
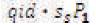from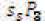 
which is considered to be very difficult. Also the attacker must has the ability to analyze the key such that to replace the identity by the identity of target. In order to do this, he/she must know the two secret keys of PKGC where he/she must find r and user from 
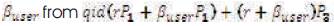to replace ID. In addition, the SEM cannot use his half key to sign message without the user help because the SEM has no enough information about the other half of the key. Thus, we can claim that our developed scheme for mediated IBS is computationally unforgeable, since it is based on a solid computational problem.
In order to use the system, the SEM and all users must obtain the public parameters from GC. When any user (Alice) wants to send the message to another one (Bob), they must execute the following procedures (Figure 3):
Figure 3. Procedure of System Operation
In the next messages of the session, Alice and Bob continue sending and receiving the messages without a need to contact with GC. This means that the same procedure is used but without steps 1 and 7.
The system has been implemented using Visual C# programming language. This language gives to programmer the flexibility to build large systems efficiently. The system uses the standard SMTP and POP3 internet protocols to send and receive emails through the email server. Anyone must have an access to an email server that supports SMTP and POP3 to use the system by creating a user account and mailbox on the server. Using the email account, together with developed secure-email software, a user can send and receive messages securely over the internet. The developed software can get email messages, store them for future reference, show them to user, let him/her organize them, and let him/her write and send own messages.
The architectural parts needed to implement this application are: SMTP, POP3, GC, SEM, and Client with suitable Graphical User Interface (GUI). The GUI must be used to provide a secure and simple means of messaging via email. These messages are received and sent using ordinary email methods (SMTP and POP3) but with adding the required security services. Each part of the developed system has its own interface to enable users or administrators to prepare the setting correctly. Figure 4 illustrates the application main window. It contains the basic options to manage the email (inbox, sent, draft) and also to display the message. When the received message is encrypted, it must be decrypted before reading. The decryption is performed directly after requesting to show the message. A flag has been added before sending to indicate whether the message is encrypted or not.
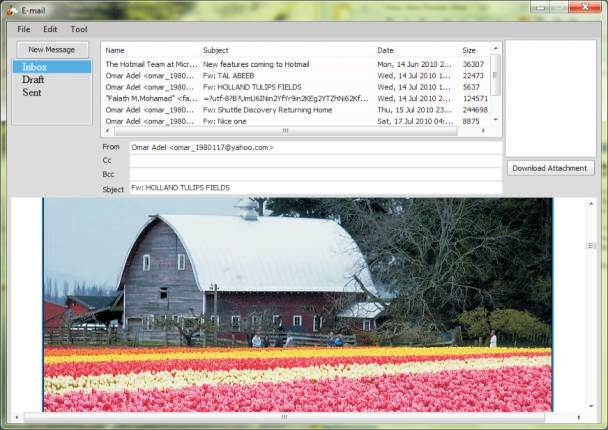
Figure 4. Main Window of the Application
The two proposed hybrid cryptographic techniques based on IBC and mediated cryptography have shown to be very promising in building secure email systems with very good usability characteristics. They both can achieve mediated IBE and mediated IBS. Using Mediated cryptography has given the designer (or administrator) a choice of keeping users under control to prevent any unauthorized person from using the system. This could be very useful for organizations and companies. Both of the developed hybrid cryptographic schemes have been of higher speed and more efficiency compared with mRSA with some additional security and/or efficiency bonus for the second proposal. In addition, the proposed secure email system does not need to use key rings for public keys of users (as in PGP) because the public key is the email address of the user.