
In this paper a synthesis approach for designing a fuzzy supervised nonlinear PID controller is considered. The objective of this work is to develop a PID based control algorithm for non linear discrete systems using the combination of non conventional and conventional control techniques. The proposed algorithm is a supervised structure, where a fuzzy supervisor provides at each sample time the suitable PID parameters. In order to improve the dynamic response of the closed loop system, the optimization of the performance of the fuzzy supervisor will be considered. Simulation is carried out for a first order non linear process and the speed control of a DC motor with serial excitation.
The proportional, integral and derivative (PID) control algorithm remains the most popular approach for industrial process control despite continual advances in control theory. This is not only due to the simple structure, which is conceptually easy to understand and, which makes manual tuning possible, but also to the fact that the algorithm provides adequate performance in the vast majority of applications.
The proposed tuning method in this paper differs from those reported methods in three aspects. First, the developed tuning algorithm is a supervised structure, where a fuzzy supervisor provides at each sample time not only a factor scale or a gain but the suitable PID parameters. Secondly, the fuzzy rule generation of the supervisor is based on an automatic method and wellknown tuning guidelines rather than heuristic and/or expert knowledge. Thirdly, the tuning method can be applied for complex non linear system.
So the objective of this paper is to develop a systematic synthesis method for PID supervisor structure. The proposed approach is essentially based on successive linearization procedure to provide a numerical data set allowing the automatic synthesis of the fuzzy supervisor.
Adding to that, to improve the behavior of the fuzzy supervisor coupled with PID controller, an optimization procedure is accomplished to minimize the output error of the closed loop system.
The arrangement of this paper is as follows. The PID control law and the whole control structure will be briefly presented in the problem formulation section. The synthesis method which is based on a linearization procedure to provide a numerical data set allowing the automatic synthesis of the fuzzy supervisor and the improvement of its behaviour using an optimization procedure are discussed in section 3. The structure of the fuzzy supervisor and the learning algorithm based synthesis are presented in section 4. The outlines of the proposed method are summarized in section 5. Simulation studies are considered in section 6. In fact, two non linear processes are treated to show the effectiveness of this new synthesis method. Finally conclusions are drawn.
Many PID design techniques have been developed in the literature see, [1-4], in fact most of the PID tuning rules developed in the last 50 years use frequency-response methods. Examples include, Ziegler & Nichols rule [5], symmetric optimum rule [6], Ziegle & Nichols complementary rule [7], some-overshoot rule [8], refned Ziegler & Nicholes rule [9], integral of squared time weighted error rule [10], and integral of absolute error rule [11]. These methods are straightforward to apply since they provide simple tuning formulae to determine the PID controller parameters. However, since only a small amount of information on the dynamic behaviour of the process is used, in many situations they do not provide good enough tuning or produce a satisfactory closedloop response.
In an effort to improve the performance of PID tuning for processes with changing dynamic properties, several automatic tuning and adaptive strategies have been proposed [12], [13]. These controllers have selfinitialisation and recalibration features to cope with little a priori knowledge and signifcant changes in the process dynamics, based on the automatic measurement of the ultimate gain and period. Various techniques, such as relay excitation feedback [1] and rule-based autotuning [14], have been developed. However, the PID controller parameters are still computed using the classic tuning formulae and, as noted above, these do not provide good control performance in all situations. In fact the limitations of these controller rapidly become evident when applied to more complicated systems such as those with a time delay, poorly damped, nonlinear and time varying dynamics. For these processes non linear control may be necessary for good control performance. Recently, a non linear PID control sheme has been deveolped for regulating hydrolic systems [15 ]. Based on a first order model, a non linear PI control has been proposed by Oh et. al. [16]. Along with these approches, non linear PID control strategies have been proposed on the bases of fuzzy control techniques. In fact, a specific interest for fuzzy logic in control has emerged during these last years. The use of such techniques is principally relevant in the following cases. First if the process model is unknown, fuzzy techniques are useful for modelling human operator knowledge [17]. Secondly, if the process model is known, fuzzy techniques can be used to improve the closed-loop performances for linear or non-linear plants [18]. When fuzzy controllers are used, the ability to generate non-linear control laws with the various degree of freedom is interesting [18]. So the most usual applications of fuzzy techniques are fuzzy controllers.
However, some of the fuzzy controller implementations lead to partially good results. Moreover, it is still difficult to study the closed-loop stability with such linguistic controllers. Other relevant applications of fuzzy techniques for tuning PID controller have been considered to push back the limits of conventional techniques and to improve to closed loop dynamical performances. In fact, many efforts dealing with tuning the conventional controllers using fuzzy logic have been reported. Bandyopadhyay et.al. [19] proposed an autotuner for PI controllers based on fuzzy logic. The method computes each sampling time new PI parameters using a scaling factor to provide dead-beat performance. The scaling factor depends on expert knowledge and thus, it is not clear how to extend the method to different type of processes. Miler et al. [20] proposed a PID tuning strategy based on fuzzy logic to control a specific bioreactor. The proposed method tunes the PID parameters online each sampling time using fuzzy rules. However, the fuzzy rules are generated from expert knowledge of the oxygen consumption in the reactor.
Therefore, this method can not be generalized easily to other processes. Chan [21] developed an automatic tuner for PID controllers based on fuzzy rules. However, the proposed method requires training the fuzzy rules using different closed-loop responses generated at different sets of PI parameter values. Ramkumar and Chidambaram[22] suggested another fuzzy self-tuning PI controller. The tuning algorithm is based on the output error signal and not on a certain performance specification. Moreover, the fuzzy rules base is generated from iterative simulation procedure implemented on the given process. Therefore, it may not work well for another process. He et al. [23] proposed another fuzzy self-tuning method. The method is based on parameterizing the Ziegler-Nichols tuning formula by a single parameter. A fuzzy inference mechanism is used to self-tune the new parameter. The method is tested only on simple linear models. Pfeiffer and Isermann [24] have also proposed a self-tuning PI controller using fuzzy logic. The two parameters of the PI controller are adapted based on two fuzzified variables of the measured overshoot and settling ratio. The method requires the current signal of the control error to estimate the two fuzzified variables. In this case, the method lacks prediction capability. S. He et al. [25] have developed another type of fuzzy supervision technique where a fuzzy system adjust only the gain of the controller. In their hierarchical approach, the fuzzy system evaluates the controlled process output and detects the possible deviation from a prescribed course, so that it can generate compensated gains. Consequently, we have reviewed a number of approaches which combine PID controllers with the fuzzy logic techniques. These fuzzy tuning PID control structures can provide the general methods of automatic tuning of the PID controllers through either the set-point modification or the gain modification. However, in spite of their individual philosophies and structural difference, all of these approaches share the same difficulty of fuzzy rule generation. Fuzzy rules in a mixed control structure must be different according to the plant and the operation conditions in which it is operated. Since fuzzy rule generation is crucial difficult and time consuming procedure, it is required to have a systematic method for constructing appropriate fuzzy rules.
In this work we are concerned with a single input single output nonlinear dynamic processes that can be described in the discret time domain by,

Where the components of the regression vector
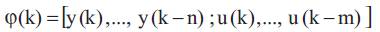
The objective of the developed method is the synthesis of a fuzzy supervisor that adjusts online the PID parameter for the control of the nonlinear processes. Therefore, a mixed control structure that combines the conventional PID with a fuzzy supervisor is used as it is shown in Figure 1. In this approach the fuzzy supervisor provides at each instant the adequate PID parameters in order to improve the dynamic response of the closed loop system.
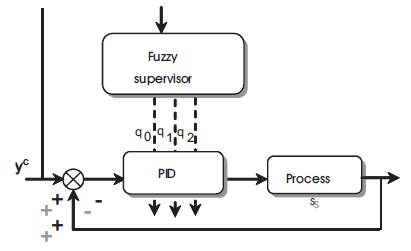
Figure 1. Control Structure
The PID controller computes the following control law [24]:
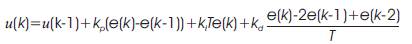
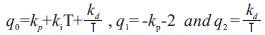 then the discret form of the PID control can be expressed by,
then the discret form of the PID control can be expressed by,
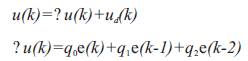
The synthesis of this supervisor is based on a learning phase. The procedure adopted to collect the training set is based essentially on linearization of the plant to be controlled at different operating points [26]. Then the practical idea is to use the pole assignment technique to determine the discrete PID parameters for different operating points.
The linearized system around an operating point (U,Y) is described by the following equation,
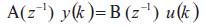
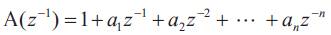
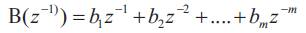
U,Y are the corresponding values of the input and the output at the permanent sate. To obtain this values, the control input is fixed to a given value, then, the corresponding process output is computed from the mathematical model, or enregistred from the simulation of the process. The parameters of the linearized model are given by,
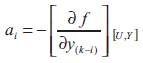
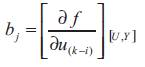
for i=1,…,n and j=1,…,m
After linearizing the system, we use the pole assignment technique to determine the discrete PID parameters. For example, in the case of a first order non linear process the corresponding PID parameter are given by:
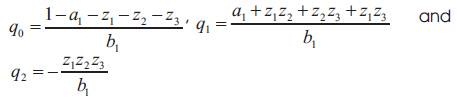
Where z1 , z2 , and z3 are the the pôle of the closed loop System
By repeating this procedure for each linearized system, a learning set is collected to identify the fuzzy supervisor parameters. The learning examples have been adjusted according to an optimization method to improve the closed loop system response.
To minimize the output error of the closed loop system, the collected PID parameters have been subject of an optimization procedure.
For each operating point, the gradient algorithm has been used to reach the optimal values which minimize the squared of the differences between the desired and the processes outputs. The following criterion is given by,
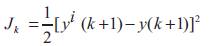
yi denote a given value around the operating point yc to enlarge the validity domain of the determined PID controller.
The adjustment procedure is given by the following expression,
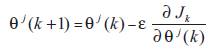
The adjustment can be stopped when the PID parameters become unchanging. So, we store the new pairs 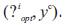 This new learning set, will be used to generate the fuzzy rules of the supervisor.
This new learning set, will be used to generate the fuzzy rules of the supervisor.
Fuzzy systems are known as universal approximator from human expertise and from numerical examples. A set of fuzzy rules can be derived to approximal desire behaviour [17]. In this investigation, a zero order Takkagi Sugeno fuzzy system [18] is considered. Its role consists on learning the correspondencies between each operating of the system to be controlled and the adequate PID parameters.
As it is shown in Figure 1, the fuzzy system has one input, which is the operating point in the learning step and the desired output in the control step, and three outputs which are the discet parameters of the conventional PID controller. Then, the pth rule of the considered fuzzy system is given by,
Rp : If Yc is Ap Then θp ; p =1,....r
Where,
‘r' is the rule number, Ap are the fuzzy sets,  are the values of the PID parameters that has been computed from the optimized data set.
are the values of the PID parameters that has been computed from the optimized data set.
The output of the fuzzy system with r rules is aggregated as
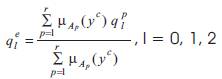
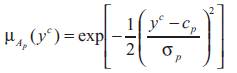
For the manual synthesis of the fuzzy supervisor, the center and the width of the membership functions are fixed manually (using the fuzzy tool books of Matlab). The consequent part of the fuzzy rules, which are the parameters of PID controller, have been taken from the learning examples set. In fact for each rule, they are the values of the parameters corresponding to a degree of truth of the condition equal to 1. However we note that the fuzzy supervisor based on the manual synthesis is not well conditioned. In fact, the performance of the closed loop system decreased in some set points.
Therefore, to improve computational accuracy of the fuzzy system, an adjustment procedure of its different parameters has been proposed.
To improve the performance of the fuzzy supervisor, the fuzzy system parameters have been subject of an updating procedure. The gradient algorithm has been used to reach the optimal value which minimizes the sum of the sequares of the errors made on the leaning set. The following criterion is given by,
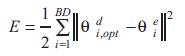
where θdi,optdenotes the desired optimal values of the PID parameters that have been computed from the optimized learning examples set. θei indicates the PID parameters provided by the fuzzy system and BD designates the size of the learning set.
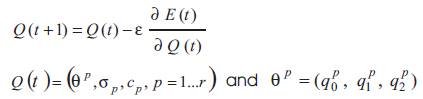
In summary, the general procedure of the synthesis of the control structure can be accomplished according to the following steps,
Step 1: Linearize the mathematical model of system to be controlled around a set of operating points.
Step 2: For each linearized model, determine the adequate PID parameters using pole assignment method.
Step 3: Adjust the PID parameters around the set optimization giving the optimized training set.
Step 4: Adjust the fuzzy supervisor parameters using the optimised training set and gradient method.
Step 5: Insert the fuzzy supervisor in the control loop.
In this section, a simulation study is conducted to demonstrate the performance of the developed synthesis method for PID supervision structure. A first order nonlinear process and a DC motor with serial excitation are used in simulation. To evaluate the performance of this control algorithm, we compare its set point as well as the load disturbance response with the PID controller tuned by the Ziegler and Nichols formula and an adaptive control design [27], [28].
The first simulation concernes a first order nonlinear process given by the following equation [29].
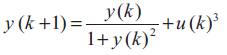
The synthesis of this supervisor is based on a learning phase The procedure adopted to collect the training set is based essentially on linearization of the plant to be controlled at different operating points (Ui, Yi). The parameter of the linearized model are given by,
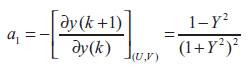
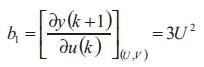
Then the practical idea is to use the pole assignment technique to determine the discrete PID parameters for each operating point.
In order to build the optimized data base we have adopted this procedure:
After many test we choose a value of a learning rate equal to 0.1 and by varying slightly at each iteration the desired output around the operating point (variation of 2.5 %), we store for each 50 iterations the value of error between the desired output and the plant output. The optimization has been stopped either when total error reaches a bottom or the gradient algorithm converges so, we store the new couples 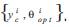 . In Figure 2, an example of optimization is presented.
. In Figure 2, an example of optimization is presented.
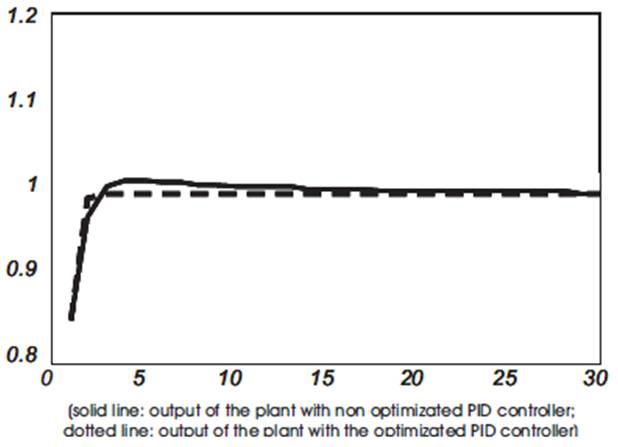
Figure 2. Evolution of the Plant's Output around the Operating Point yc=1
The error between the desired output yc =1 and the plant output of the closed system stored for each 20 iterations is given by Figure 3.
The optimized learning set is used for the off-line initialization of the fuzzy supervisor.
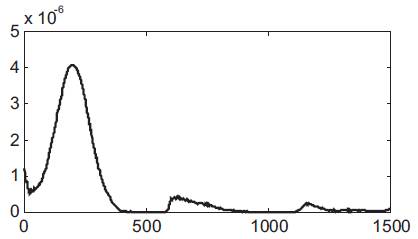
Figure 3. Error Evolution during Optimization Procedure
The initialisation of the fuzzy supervisor was accomplished by the learning algorithm described by equation (14). The fuzzy supervisor had one input y*(k+1) and three outputs which are the estimated value of the PID parameters. The input variable (denoted y*(k+1) is either the output of the plant (in the learning phase) or the desired output in the control operation. Five fuzzy sets were associated for this input. The consequent part was considered as a zero order Sugeno model.
Once an accurate fuzzy supervisor has been well trained off line, it can be inserted in the control loop.
Simulation results are shown in Figure 4. As seen in the simulation plots there is considerable reduction in the peak deviation in the response curve obtained with the proposed PID tuning method as compared with response curve obtained through the adaptive PID control algorithm and although there is no substantial improvement in the rise time. Added to that, in Figure 5, we note that with load disturbance the proposed tuning method makes the response settle faster than the other controller and hence the performance improves.
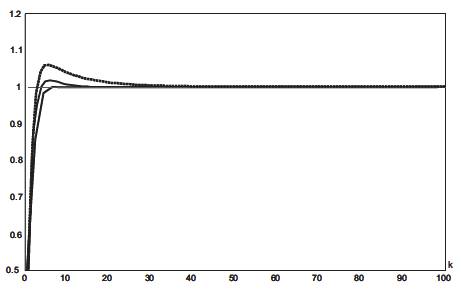
Figure 4. Evolution of the system output : dashed line (…) : adaptive tuning method, solid line (-) proposed method
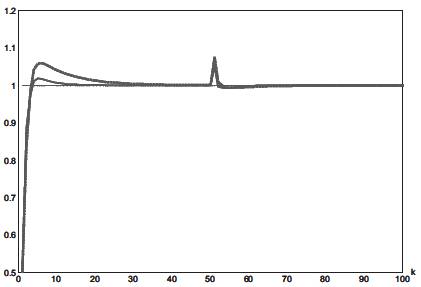
Figure 5. Evolution of the System Output : dashed line (…) : Adaptive Tuning Method, Solid Line (-) Proposed Method
The proposed algorithm has been tested on a DC motor with serial excitation. Its simplified mathematical model can be represented by the following differential equation [30]:
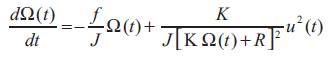
The voltage u (t) is taken as the control input and the motor speed ?(t) as the output of the system. The motor parameters have the following values:
The resistance R = 2500 Ohm, friction f =7 10-8 N.m/rad.s-1 , iniertia of rotor: J = 17 10-8 Kg.m2 , constant of the motor: K = 2.6 V/ rad s-1 .
Using the Euler approximation method, the discrete system can be expressed by:
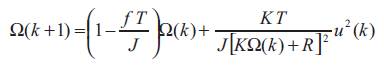
Let consider an operating point characterized by (?0 ,u0 ). The linearized system is given by the following expression:
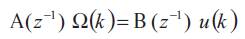


After linearizing the system around an operation point, we have defined the corresponding discrete PID parameters using the method of pole assignment. Thus, we have constructed the learning set composed by the pair 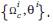 . The optimization of these learning examples has been accomplished by the following procedure:
. The optimization of these learning examples has been accomplished by the following procedure:
After many test we choose a value of a learning rate equal to 0.01 and by varying slightly at each iteration the desired output around the operating point (variation of 10%), when the error converges finally toward zero, we store the last values obtained after stopping the adaptation, then one passes to another operating point. Thus we built the optimal learning set.
The proposed fuzzy supervisor had one input ?0 (the desired motor speed) and three outputs (the estimated parameters of the PID controller). Some simulations have been conducted giving a fuzzy rules number equal to five.
The response of this algorithm is compared with the Ziegler Nichols PID controller and adaptive PID controller. Responses are shown in Figure 6 and 7. The disturbance to the process is assumed to be a sudden variation of the motor resistance value at t=10 s. As it is shown in the curve the proposed tuning method performs better than the conventional PID controller tuned with Ziegler Nichols formulas and an adaptive PID control algorithm [28].
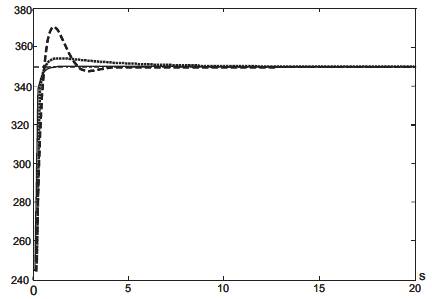
Figure 6. Evolution of the system output : dashed line (…) : adaptive tuning method, solid line (-) proposed method, dotted line (- - -) : Ziegler&Nichols tuning method
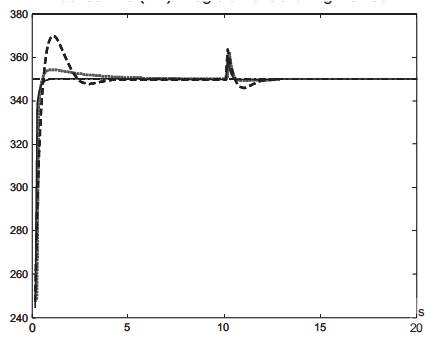
Figure 7. Evolution of the system output :dashed line (…) : adaptive tuning method, solid line (-) proposed method, dotted line (- - -) : Ziegler&Nichols tuning method
The present work presents a synthesis approach for designing a fuzzy supervised non linear PID controller. The proposed control scheme has superior performance compared to a conventional PID controller. An advantage of the proposed approach is that.
The results on a first order nonlinear process and a DC motor with serial excitation demonstrate the robustness and the good performances of this control algorithm. This paper supports the design philosophy that fuzzy logic can be used effectively to assist conventional control methods for improving performance especially in the presence of unknown and several nonlinearities.