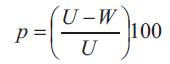
Placing a set of activities or jobs along a timeline is known as scheduling. The interval scheduling problem arises when each job is specified by an interval with starting and finishing times of each job. It will become a weighted interval scheduling problem when a weight or a value is associated with each job. In this paper, the aim is to maximize the total weight of the jobs that could be scheduled without overlapping. A fast algorithm is presented to solve this problem. An upper bound for the total weight is computed and it is shown that the gap between the solutions to the test problems and the upper bound is extremely small.
Weighted interval scheduling problem differs from the basic interval scheduling problem by attaching a weight to each job in addition to starting and finishing times for each job. Here, it is necessary to find the subset of jobs which carries the highest weight, so that no job overlaps. Weighted interval scheduling problem is an extension of the basic interval scheduling problem. The basic interval scheduling problem consists of scheduling n jobs each with given starting and finishing times so that no overlapping occurs. It is assumed that each machine can process atmost one job at a time and machines are available without restriction. Every job is processed in the same machine until completion without interruption.
In the weighted interval scheduling problem, in addition to the starting and finishing times for each job, a weight for each job is also specified. For each job, a fixed processing interval is given. A job can be processed only in one of the given intervals on one of the available machines or is not processed at all. The goal is to select a subset of non-overlapping jobs which gives the maximum possible sum of weights.
The weighted interval scheduling problem arises in various practical situations. Some of them are bandwidth allocation of communication channels, computer wiring, printed circuit board design, and work planning for personnel.
Some of the applications can be found in printed circuit board manufacturing (Crama et al., 1997), time constrained scheduling (Bar-Noy et al., 2001), and in caching (Torng, 1998), where cache is a small, fast memory that can temporarily store arbitrary memory items so that the CPU can access them faster than in main memory.
The paper is organized as follows: In section 1, a summary of related literature to the weighted interval scheduling problem is presented. Objectives of the study and the methodology is given in section 2. In section 3, a description of the type of weighted interval scheduling problem considered here is presented. Computation of the upper bound is described in section 4. In section 5, the method of determining the quality of solutions is discussed. A numerical example is given in section 6. Result and discussion is presented in Section 7. The conclusion is given in the last section.
In this section, some of the literature related to the weighted interval scheduling problem is presented.
Arkin and Silverberg (1987) proposed an algorithm which maximizes the value of jobs completed by several identical machines.
Kroon, Salomon, and Van Wassenhove (1995) studied another variation of this problem. For each job, in addition to fixed starting and finishing times, a priority index and a job class were given. The objective is to find an assignment of jobs to machines with maximal total priority. They have presented some algorithms to solve this problem with some computational results.
Chen, Hassin, and Tzur (2002) considered the reservation of bandwidth of a communication channel of fixed capacity. The request is characterized by the required period of allocation, its required bandwidth, and the profit of accepting the request. The problem was to decide which requests to accept so as to maximize the total profit.
Erlebach and Spieksma (2003) have proposed 2- approximation algorithm for unit weights and an 8- approximation algorithm for arbitrary weights.
Another variation has been studied by Bar-Yehuda et al. (2006) in which the jobs are given as groups of nonintersecting segments on the real line. The objective is to schedule on a single machine, a subset of nonconflicting jobs whose total weight is maximum.
Kolen et al. (2007) presented a survey in the area of interval scheduling. It reviews the complexity and approximability of different variations of the interval scheduling problem. It also gives an overview of applications of the problem.
Kovalyov, Ng, and Cheng (2007) presented a general formulation of the interval scheduling problem and conducted a survey on existing models.
A variation of the weighted interval scheduling problem was studied by Darmann, Pferschy, and Scxhauer (2010), where each job has a given profit and a specified resource consumption. The goal was to select a subset of jobs with maximal total profit such that the total resource consumption does not exceed the given resource capacity at any point in time.
The aim of the study is to present a fast algorithm to solve the weighted interval scheduling problem. The objective is to maximize the total weight of the jobs that could be scheduled without overlapping.
The methodology used in developing the algorithm is a greedy approach. A one-pass algorithm is constructed using this approach, which leads to a fast algorithm.
Scheduling problems are usually formulated using machines or processors and jobs. The machines or processors represent resources and the jobs represent relevant tasks to be carried out.
Suppose that a set of intervals of the form [si , fi ) are given, where si < fi for i = 1, 2, .., n. Each interval represents the starting time and finishing time for a given job i. Also, it is assumed that each job has a weight vi . The objective is to determine a non-overlapping subset of jobs with the maximum possible sum of weights.
For example, suppose one CPU is available which can process one job at a time and it is necessary to maximize the value of the jobs that are scheduled.
Given a set of n intervals [si , fi ], each with a value vi , it is necessary to choose a subset S of non-overlapping intervals with Σi∈SVi maximized so that none of the intervals overlap.
An algorithm is presented which will make use of the length of the time interval and the weight or value of each job. In order to do this, a ratio ri is computed where,
ri = weight of job i/duration of job i.
Then, the ratio ri for each job is arranged in the descending order. This will give the weight of each job per unit time interval. First, the job having the highest ratio ri is scheduled. A schedule is constructed by placing the other jobs according to the descending order of ri, whenever possible. The jobs which will overlap if they are scheduled are not considered. That means, these jobs are rejected. The steps of the algorithm are given below.
(1) Compute weight/duration (ri ): ratio for each job i.
(2) Arrange the jobs according to the descending order of ri .
(3) Start scheduling with the job having the highest ri and place other jobs in the descending order so that a feasible schedule is obtained.
(4) Compute the total weight by adding the weights of individual jobs that has already been scheduled.
As the problem considered here is a maximization problem, in order to determine the quality of solutions obtained, it is necessary to compute a reasonably tight upper bound. It is attempted to find such an upper bound by making use of the ratios ri already computed for each job i. Again the list of ratios already placed according to the descending order is considered.
At this stage, it is assumed that the given set of jobs have already been scheduled and the total weight of the schedule has been found. A list of the jobs that have not been scheduled so far is recorded. These jobs are kept in the descending order of the ratios ri already calculated. Now, it is necessary to keep track of the free time slots by counting the number of free time slots, after scheduling.
There will be some free time slots after scheduling of jobs is completed. For the purpose of computing the upper bound, it is assumed that all these free time intervals are available. Out of these intervals, the one with the longest free time interval t is picked.
Let k be the job with the highest remaining ratio rk . Let gk = fk - sk = duration of job k.
If t ≥ gk then it is assumed that the job k can be scheduled (even though the job k has not been scheduled) using the free time slots. Now, it is assumed that the job k has been scheduled and adjust the total weight accordingly. After this exercise, the number of free time slots has been reduced to (t – gk ). Then, try to include the next job with the highest ratio in the same manner.
Then, the total weight obtained in this manner is considered as the required upper bound.
(1) For each job i, compute the ratio ri = weight/time interval.
(2) Arrange the jobs according to the descending order of the ratio ri .
(3) First schedule the job with the highest r along the timeline. Then gradually schedule other jobs according to the descending order of r so that a non-overlapping, feasible schedule is obtained. If any job overlaps with other jobs, leave it without scheduling.
(4) The total weight of the scheduled jobs gives the solution.
(5) Computation of upper bound: let t be the longest free time interval available after the above assignment of jobs. Let k be the job with the highest remaining ratio rk . Let gk = fk - sk = duration of job k.
(6) If t ≥ gk then, assume that job k is scheduled and adjust the total weight. Now, the number of free time slots has been reduced to (t – gk ). If t < gk , move to the next job with the next higher ratio. The final total weight obtained in this manner is the required upper bound.
Now, the method of determining the quality of solutions is discussed. Let W be the solution to a given problem and U be the corresponding upper bound. Upper bound indicates the highest possible value for the total weight with respect to scheduling of a given set of jobs. Value of the optimal solution shall be less than or equal to the value of the upper bound. Let K be the value of the corresponding optimal solution.
Then, U ≥ K ≥ W
Let
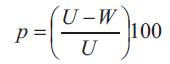
Then, p is the percentage gap between the upper bound and the solution obtained. Therefore, the optimal solution lies within p% of the best upper bound.
In this section, an example to illustrate how to maximize the weights of a given set of jobs is presented. The problem consists of 10 jobs as given below (Table 1).
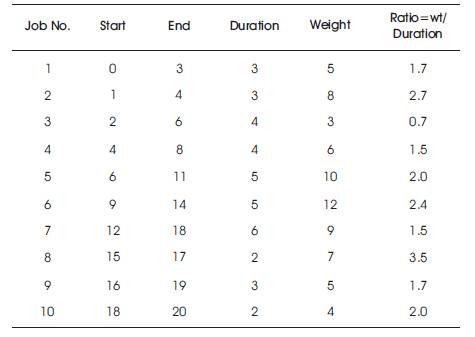
Table 1. Data for Sample Problem
The feasible combinations of jobs are given below:
(1) (0,3) :5 ; (6,11): 10; (12,18): 9; (18,20) : 4 ; total weight = 28
(2) (0,3) : 5; (4,8): 6; (9,14): 12; (15,17): 7; (18,20): 4; total weight = 34
(3) (1,4) : 8 ; (4,8) : 6; (9,14) : 12 ; (15,17) : 7 ; (18, 20) : 4; total weight = 37
(4) (2,6) : 3 ; (6,11) : 10; (12,18) : 9 ; (18,20) : 4 total weight = 26
From the above, it can be seen that the best solution having the total weight 37 is given by (3).
In this solution, 16 time slots have been used up by the jobs having numbers 2, 4, 6, 8, and 10. The number of free time slots is 4, but the longest free time interval is of length 1. There are no unscheduled jobs with length equal to 1, so the weight cannot be increased any further. Therefore, the upper bound is also 37.
In order to test the effectiveness of the proposed algorithm, several sets of test problems have been generated. The test problems containing various number of jobs were considered with varying start times, finishing times, and weights. The problem sets contained 5 to 50 jobs. The upper bound was also computed for each problem.
The results are given below (Table 2). The total weight obtained for each problem and the upper bound is given. Figure 1 gives the comparison of total weights of test problems with upper bounds.
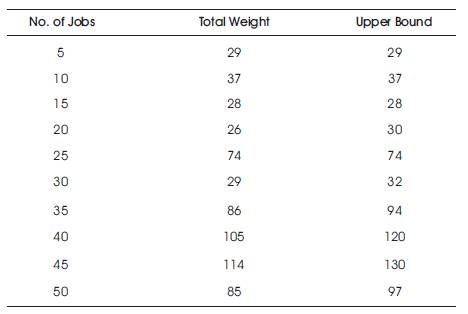
Table 2. Total Weights and Upper Bounds for Test Problems
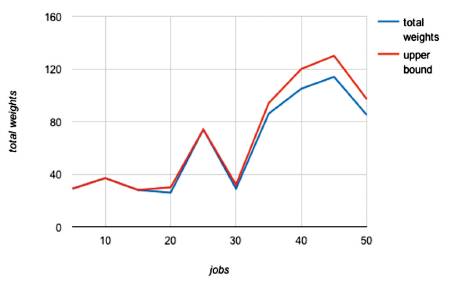
Figure 1. Comparison of Total Weights with Upper Bounds for Test Problems
From the above results, we can see that the total weights with respect to each problem set lies close to the values of upper bounds. It can also be observed that the gap between the solutions and the upper bounds vary as the problem size changes. However, the gap appears to be very small in many cases. For certain problems, there is no gap at all which means that the solution coincides with the upper bound, indicating that the optimal solution has been reached in these cases.
Therefore, it can be observed that these results could be applied even in situations where problem size is large. However, to refine these results it is necessary to apply the proposed algorithm for larger number of test problems.