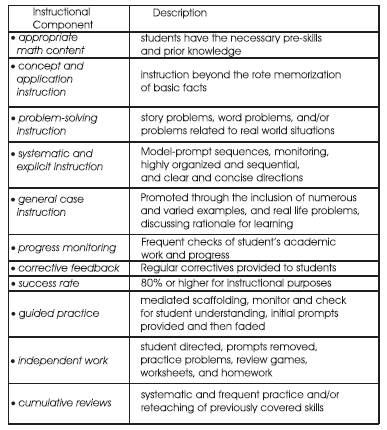
figure 1. Components of effective mathematics instruction.
This paper is an analysis of published research on computer-assisted instruction [CAI] for mathematics involving students with learning disabilities. A systematic search of the literature on computer-assisted instructional interventions for students with learning disabilities yielded 25 studies that met the criteria for inclusion in this analysis. The studies were analyzed on an identified set of evidence—based instructional components validated in the effective teaching research. Overall, the results suggest that most of the identified evidence—based instructional components are incorporated into CAI programs used to teach mathematics to students with learning disabilities. Additionally, the results indicate that CAI is a generally effective means for increasing the mathematical performance of students with learning disabilities. Although promising, the implications for practice based on this analysis are limited by the relatively small number of studies reviewed and the diverse array of mathematical concepts and skills targeted. Findings from this analysis highlight the need for continued development and research validation of CAI programs focusing on improving learning outcomes of students with learning disabilities.
In 2005, the national assessment of educational progress [NAEP) reported that U.S. students are alarmingly deficient in their mathematical problem-solving skills. Approximately half of 12th grade students could only solve problems past whole-number computation [National Center for Educational Statistics, 2005). Overall, the mathematics performance of students in the United states is deficient. Even more troubling is the fact that students with disabilities have greater deficits in their mathematics performance than their peers.
Students with learning disabilities (LD) experience difficulties in learning math, with problems surfacing early and continuing throughout a student's education [Bottge, 1999; Witzel & Riccomini, 2007). Deficiencies in mathematics performance are not limited to basic mathematics skills. Higher order thinking skills such as problem-solving are also a major problem for students with LD (Bottge, Reuda, Larouque, Serlin. & Kwon, 2007). Furthermore, students with LD have documented deficits in the areas of basic facts, subtraction, solving word problems. Acquiring concepts, and problem-solving skills(Sanders, Riccomini, & Witzel, 2005). This is particularly Alarming because other skill areas rely an arithmetic skills [e.g.. Science) and basic computational skills are a fundamental prerequisite for persons seeking employment in an increasingly competitive employment market.
While there are many plausible explanations for the poor mathematics performance of students with LD, one explanation is the instruction being delivered (Bost & Riccomini, 2007). Typically, math instruction has three structures: teacher lecture or demonstration, guided practice, and independent practice. The majority of time should be allocated to the initial demonstration and guided practice, with students only moving on to independent practice when they perform at an 80% success rate(Rosenshine & Stevens, 1986). effective mathematical instructional practices used by effective teachers must be carefully examined.
It is clear from the research on students‘ mathematical performance that the instruction they obtain is often not effective in meeting their instructional needs (e.g., poor student outcomes). Inadequate instruction is a contributing factor in children failing to learn basic academic skills. Clearly, instruction that is more effective should produce better math achievement. A number of empirically validated instructional techniques have been identified for general instruction and specifically for mathematics.
Rosenshine and Stevens (1986) promote five teaching behaviors necessary for effective instruction. The general lesson model includes (a) review and check previous day's work; (b) present new content: (c) guide student practice and check for understanding; (a) provide feedback, correctives, and reteach if necessary; and (e) provide weekly and monthly reviews. These teaching behaviors are reflected in the model of explicit instruction advocated by Gersten and his associates, who articulated six instructional variables (Gersten, 1985,‘ Gersten, Carnine, & Woodward, 1987). The instructional variables include (a) explicit step-by-step problem- solving strategies, (b) emphasis on small group instruction as opposed to students working alone, (c) systematic correction process for student errors, (d) highly structured practice faded to a level of independent practice, (e) a range of well conceived examples with adequate practice, and (f) cumulative review of concepts (Gersten, 1985,‘ Gersten et al., 1987).
These teaching behaviors and instructional variables apply to all instruction and are similar to those advocated specifically for mathematics instruction by several researchers [e.g., Jitendra & Xin, 1997; Miller & Mercer, 1993). Miller & Mercer, 1993) compiled a list of ten components of effective math instruction. The ten components are consistent with the literature completed in the last decade, which indicate that both curriculum design and teacher behavior directly influence the mathematics achievement of students with learning problems. The ten identified effective instructional components for mathematics instruction are: (a) selecting appropriate math content, (b) establishing goals and expectations, (c) providing systematic and explicit instruction, (d) strategically teaching math concepts, (e) monitoring student progress, (f) providing corrective feedback, (g) teaching to mastery, (h) teaching problem solving, (i) teaching generalization, and (j) promoting positive attitudes toward math.
Clearly, both general as well as math—specific instructional principles share common procedures. For the purpose of this study, the authors adapted the instructional components identified by Gersten (1985), Rosenshine and Stevens (1986), and Miller & Mercer, 1992). thus, the features identified for the current research include the following eleven instructional components: (a) appropriate math content, (b) concept and application instruction, (c) problem-solving instruction, (d) systematic and explicit instruction, (e) instruction for broadening the case, (f) progress monitoring, (g) corrective feedback, (h) high success rate, (i) guided practice, (j) independent practice, and (k) cumulative review.
It is the responsibility of all educators to design and deliver instruction based on the considerable research available specific to the above listed effective instructional practices. Those charged with the responsibility of mathematics education must realize that the delivery of inadequate instruction is at least partially responsible for the deficient mathematical performance of students in U.S. schools. Instruction that is validated and more effective should produce better student mathematical achievement. Therefore, teachers must incorporate these 11 instructional components to maximize instructional effort and outcomes with students of all abilities.
Some educators and administrators believe that technology is one possible remedy for the poor mathematical performance of students with disabilities. Instructional technology has the potential to assist and improve teachers‘ ability to individualize instruction, provide immediate and continuous feedback, maximize functional practice, better motivate students to learn, and ultimately improve students‘ mathematics performance. Access to technology in schools is increasing resulting in computer-assisted instruction (CAI) emerging as an alternative delivery system for teaching and supplementing traditional math instruction. Computers, computer software, and videodisc technology offer a promising medium through which mathematics instruction and practice opportunities can improve. Computer-assisted instruction is used extensively to teach or provide practice of mathematics skills for students with disabilities (Hughes & Maccini, 1997). Educators have used CAI to teach basic facts as well as problem solving, telling time, ratios and proportions, fractions, and decimals.
Based on an extensive literature review on CAI and mathematics, Hughes and Maccini (1997) reported that the use of CAI can increase students‘ mathematical performance. More importantly, Hughes and Maccini (1997) concluded that: [a] computer—based programs utilizing specific design features more effectively increased students‘ mathematics achievement than traditional basal instruction, [b] CAI and teacher directed instruction with effective design principles were equally effective, and (c) instruction delivered via videodisc increased students‘ problem-solving skills. Logically, CAI programs used to teach mathematics skills that are based on effective instructional principles, increase students‘ mathematics achievement.
Researchers, educators, and practitioners are investigating numerous educational reform practices to improve the deficient mathematics achievement of students with LD. For example, some researchers have focused on the areas of assessment, curriculum, curriculum integration, learning styles, instructional design, and technology. The focus of this paper is to examine the use of the eleven essential instructional design components in computer-assisted mathematics software.
Considering students‘ poor mathematics achievement and the limited time available to instruct students with disabilities, educators require effective and efficient instructional practices. Teacher instruction with the addition of CAI could be an effective and efficient procedure for teaching students with disabilities. Therefore, it is important to determine if effective instructional practices advocated for teacher—deiivered instruction are also effective when incorporated into cai programs. One could hypothesize, the CAI programs including more of the 11 identified effective instructional components would be more likely to result in improved mathematics achievement for students with disabilities (see figure 1 ].

figure 1. Components of effective mathematics instruction.
The purpose of this paper is to review the literature on CAI programs to address four questions. First, is CAI an effective means for increasing students‘ mathematics achievement? Second, how many of the 11 identified instructional components are used in the CAI programs? Third, are some of the 11 identified instructional components used more frequently than others? Fourth, are CAI programs that use more of the 11 instructional components more likely to produce significant gains in students‘ mathematics performance than programs that use fewer components?
Inclusion of studies in this analysis was determined by four criteria, the study: (a) examined the effects of a computer-based intervention on students‘ mathematics performance, (b) included students with special needs [e.g., LD, ED, MR), (c) demonstrated design of an empirical study, and [d) was published in a refereed journal. A thorough electronic search of the Educational Resources information Center (ERIC) and the PsychInfo databases was conducted. the keywords used in the electronic search were [math instruction and computer- assisted instruction] and [learning disabilities or disabilities]. The search yielded 25 articles that satisfied the above stated criteria (see table 1 ).
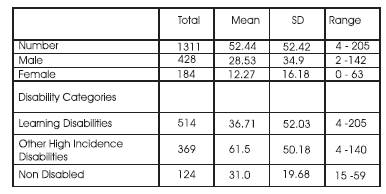
Table 1. Participant information
Each research article that met criterion for inclusion was systematically analyzed in relation to the 11 essential instructional components of mathematics instruction adapted for this research described in figure 1. An evaluation rubric was used to assess the presence of the instructional component in each article. If the instructional components were not clearly described to determine specific components, the article was excluded from this review. After the initial analysis, a reliability check was conducted on each study. an independent scorer was trained on the definitions and criterion for the 11 instructional components and independently analyzed each article. The percent of simple agreement ranged from .82 to 1.00 with a mean of.94.
The results of this analysis are presented in four segments for the 25 studies meeting the research criterion. First, the researchers provide an overview of the participants in the 25 studies, the mathematical skills taught, and the technology used. The second segment examines the effectiveness of CAI. In the third segment, the number of instructional components used in each study is described. Fourth, the relationship between significant gain in mathematics achievement and the number of instructional components used in the cai programs are presented.
Participants in each study included students with learning disabilities, emotional/behavioral disorders, students identified as mentally retarded, and students considered at-risk by the school. Eighteen of the 25 studies included students with learning disabilities. Participants ranged in age from 7 — 18years [see table 2).
Atotal of 1,311 students participated in the studies evaluated. All participants in the research reviewed were school-aged students ranging from grade one to twelve. An additional three researchers have also included first and second grade participants, 5 studies focused on 4 to 6 grade students. Three researchers included participants from the range of elementary level students (grade 1-5), six studies included students from the middle school grades. One study included participants from grade one to 8. There were 3 studies with a focus on secondary grade [grades 9-12) students. Four studies did not report student age or grade.
The majority of studies focused on intervention impact for students with disabilities. Ranges of disability types were noted in varying studies (see table 2). In some studies, students from general education setting were participants of the research. These students were usually in control groups. In all 25 studies, the primary focus of research was the improvement of the participants‘ mathematical skills.
A variety of math skills were targeted in these studies, and included basic facts, computation, decimals, fractions, time telling, and problem solving. Basic facts and problem solving were the focus of the majority of studies. Ten studies targeted problem solving skills and eight studies focused solely on basic facts.
Twenty studies used a conventional computer, monitor, and keyboard. Four studies used videodisc. The remaining study used a combination of videodisc and conventional microcomputers. Fourteen studies were designed to compare teacher-delivered instruction to CAI (56%). Nine of these fourteen studies had results favoring the CAI groups. Four studies had equivalent results for CAI and teacher—delivered instruction. Researchers from only one study (Wilson, Majsterek, & Simmons, 1996) reported that teacher-delivered instruction was better than CAI (see Table 2).
Twenty-five studies met criteria for inclusion in this study (see Table 2). students‘ mathematics performance in the CAI groups significantly increased from pre-test to post- test in 21 studies. Two studies (Woodward, Carnine, Gersten, Gleason, Johnson, & Collins, 1986; Bahr & Reith. 1989) had no significant gains from pre-test to post—test for CAI students. In two studies (McDermott & Watkins, 1983; Wilson, Majsterek, & Simmons, 1996), the authors did not specify if CAI participants had significant gains from pre- test to post-test.
The 25 studies varied in their application of the 11 instructional components that ranged from 3 to ii (m 8.52). Ten (40%) of the CAI programs used in all 11 instructional components were identified as effective and efficient for mathematics instruction. Nine of these 10 studies(Chiang, 1986; Friedman, et., al, 1984: Gleason. et al., 1990 Kelly, et al., 1986: Mastropieri, et al., 1997, Miller, et al., 1984; Trifiletti, et al., 1984; Bottge, 1999; Bottge, eta|., 1993) reported significant gains for students' mathematics performance from pre-test to post-test. in the remaining study (Woodward, et al., 1986), students did not change significantly from pre-test to post-test.
Nine (36%) of the 25 studies employed a CAI program that used between 6 and 10 of the instructional components. There were significant gains in mathematics performance from pre-test to post—test for students receiving CAI instruction in eight of these nine studies (Shiah et al., 1995; Hasselbring et al., 1988; Koscinski et al., 1993; Moore, 1988; Watkins et al., 1981,‘ Podell et al., 1992; Lin et al., 1994; Okolo, 1992b). In the remaining study(Wilson, et al., 1996), the authors did not specify if the CAI students‘ mathematics performance significantly improved from pre-test to post—test.
Six (24%) of the 25 studies employed a CAI program that used between 3 and 5 of the 11 instructional components. Students instructed with these CAI programs had significant achievement gains from pre-test to post- test in four of these six studies (Bahr, et al., 1991; Christensen, et al., 1990 Lieber, et al., 1987; Okolo, 1992a). In the study by Bahr and associates (1989), students in the cai program did not have significant pre- test to post—test gains. in the remaining study (Mcdermott, et al., 1983), authors did not report if participants in the CAI programs demonstrated gains from pre-test to post—test, rather, group comparisons were reported.
Each study was analyzed for their use of the eleven instructional components in mathematics. Appropriate content, progress monitoring, and functional independent practice were identified as utilized in all 25 studies. Guided practice and cumulative review were identified in 21 (84%) of the CAI studies. Corrective feedback and success rate were incorporated in 19 (76%) of the CAI studies. In 16 (64%) studies, systematic and explicit instruction was utilized, while generalization instruction was incorporated into 15 (60%) of the CAI studies. Concept and application as well as problem solving components were identified in 12 (48%) of the CAI studies (see table 3).
The 25 CAI programs varied little in the outcomes for students‘ mathematics performance. Moreover, achievement gains appear unrelated to the number of instructional components used in the CAI. Twenty-one studies had positive gains, two studies did not, and gain from pre-test to post—test was not reported in one study. Moreover, those studies that did produce positive effects used between three and eleven of the instructional components. The two studies not obtaining positive outcomes used 3 and 11 instructional components respectively. The pearson product-moment correlation coefficient between the number of instructional components used and the presence or absence of significant gain in achievement was -0.14, a value not significantly different from 0.
The poor mathematical achievement of students with disabilities and the limited instructional time has created a need for educators to use more effective and efficient instructional practices. With advances in technology, one possible solution is for teachers to supplement their mathematics instruction with computer-assisted instructional software. Therefore, the purpose of this paper is to review the literature focusing on mathematics CAI programs. Overall the findings suggest that CAI is a generally effective means to increase students‘mathematics performance. However, the number of the eleven instructional components used varied widely and appeared unrelated to student outcomes.
The findings and conclusions must be tempered by four factors. First, the present analysis focused solely on the subject area of mathematics although CAI has been used in a variety of subject areas. Second, the present analysis focused on CAI programs used with students with disabilities. Third, the researchers imposed the 11 effective instructional components analysis on each study. The descriptive details of the CAI programs varied. In some cases, there may be inaccuracies in the number of instructional components analyzed. Fourth, some of the CAI studies had a limited instructional focus (e.g., addition facts) reflected in the outcome measures, thus causing a ceiling effect that may have inflated the outcomes. These final two limitations may account for the studies that had positive gains, but used fewer of the 11 instructional components. However, these limitations were taken into consideration in the development of the conclusions for this research. Four findings are discussed in the following section.
First, the findings of this analysis support the conclusion that CAI is a generally effective means of increasing students‘ mathematics performance in the area of basic facts, time telling, computation, fractions, and problem solving. This finding is of particular interest because of the poor mathematical performance and recent emphasis placed on these skills by states and local districts; evidenced by the requirement of all high school students to achieve minimum standards on math assessments [Maccini & Gagnon, 2000). More importantly, students with disabilities were able to learn a variety of mathematical skills that have been shown to be extremely problematic. The improvement of mathematical performance of students instructed with CAI should encourage educators to implement CAI with their mathematics instruction.
Second, the results of this study indicate that the 25 CAI studies varied in their application of the 11 dentified instructional components. Two possible explanations for the limited use of the 11 effective instructional components seem plausible: (a) the individuals designing computer-assisted instructional programs may lack information about instructional pedagogy or (b) CAI programs require only certain combinations of the 11 instructional components to produce positive gains. The latter explanation is supported by the finding that CAI is a generally effective means of increasing students‘ mathematics performance.
Third, the results of the present analysis indicated that 3 of the 11 identified instructional components were utilized in all 25 CAI studies. The 3 instructional components used were appropriate content, progress monitoring, and functional independent practice. This finding suggests that significant gains are likely when students have the necessary pre-skills, progress monitoring is initiated, and opportunities for appropriate independent practice are provided by the CAI program. Thus, the 11 identified instructional components advocated by researchers do not appear equally important in promoting student achievement in mathematics. Further research is needed to clarify the individual and interactive effects for each of the 11 identified instructional components on mathematics achievement.
fourth, the number of 11 identified instructional components used in the cai programs varied widely (3 to 11 ) among the 25 studies. even though the studies varied in the number of instructional components used, nearly all of the studies (n=2i] reported significant gains for students instructed with CAI. this finding does not support the general view that instruction which incorporates more effective instructional components will result in greater gains (e.g., gersten, 1985; mercer & miller, 1992; rosenshine & stevens, 1986). this could mean that cai programs require only certain combinations of the 11 instructional components to produce positive student gains. for example, when explicit instruction is used, periodic review may not significantly contribute to the instructional effectiveness; however, periodic review may be a powerful contributor in the absence of explicit instruction. further research should investigate the effectiveness of each instructional component when used in combination with other components.
The major findings of the present analysis are that when effective instructional design principals are incorporated into math focused computer-assisted instructional programs, students‘ math performance is improved. One plausible explanation for this result is students are more engaged when completing math problems while working on a computer. The increased student engagement from working on a computer positively impacts student learning. A more specific explanation backed by the present analysis is certain fundamental effective instructional components used to teach mathematics by a teacher are also effective when delivered through a computer program. Whatever explanation one chooses to explain why computer—assisted instructional programs are effective, both the present analysis and previous research suggest that students with learning disabilities might profit from some form of computer—assisted instruction for mathematics. Teachers should strongly consider incorporating and/or supplementing their current math instructional programs with computer- assisted instructional programs designed around effective instructional components.
The findings of this literature review support the use of CAI programs to improve mathematics instruction and performance of students with disabilities. However, the findings do not support the need for all it identified effective instructional components to be used in order to produce positive student gains. Researchers need to continue investigating the use of CAI programs to teach students with disabilities. The results of the continued research can be used to develop, design, and implement more effective and efficient CAIprograms.