A test is a tool that measures a construct. For instance, the gas gauge in an automobile is a test that shows the amount of gas in the tank. Likewise, a language proficiency test is a gauge that is supposed to show with precision the amount of language knowledge (called construct) that resides in the mind of the test taker. However, “if we gave the same to the same student several times, we should probably find that the student did not always get exactly the same scores. These changes in scores are called variations or variances. Some of these variations in score might be caused by true or systematic differences such as the students' improvement in the skill being tests (i.e., improvement of construct), and others might be due to error, that is unsystematic changes caused by, for example, students' lapses in concentration, or distracting noises in the examination hall” (Alderson, Clapham, and Wall, 1995, p. 87). Therefore, the aim in testing is to produce tests that can measure systematic rather than unsystematic changes, and the higher the proportion of systematic variation in the test score, the more reliable the test is. A perfectly reliable test would only measure systematic changes. As such, reliability is the precision with which a test measures what it strives to measure.

By reducing the causes of unsystematic variation to a minimum, test constructors can produce ever more reliable tests. For example, they must make sure that the test is administered and marked consistently, that test instructions are clear, that there are no ambiguous items, and so forth. Although it is impossible in practice to develop perfectly reliable tests, in theory it is possible. A primary step in ensuring test reliability is to identify the construct to be measured as clearly as possible; this is called construct definition. For a test that measure language proficiency, for example, the construct is language proficiency. A clear definition of what comprises language proficiency (i.e., construct definition) can inform the construction of reliable tests that measure language proficiency. In defining the construct to be measured, testing experts are supposed to identify as closely as possible the sources of systematic and unsystematic changes in the construct (i.e., sources of variance or variance components).

Over the past few decades, there have been several camps of testing and measurement specialists who have attempted to shed light on the sources of variance, both systematic and unsystematic, that can affect test reliability. These camps have adopted well-known names that have become part of the history of measurement and testing. In connection to language testing, there are four such camps: Classical Test Theor y (CTT), Generalizability Theory (G-Theory), Item Response Theory (IRT), and Differential Item Functioning (DIF). This paper attempts to familiarize the readers with such reliability camps.

Upon hearing the term 'classical testing theory', one might simply think that he will be presented with an antique idea like that of Plato's Utopia. The case is, however, different in the field of language testing. The most important consideration in designing and developing a language test is the use for which it is intended so that the most important quality of a test is its usefulness. Traditionally, the model of test usefulness included such test qualities as reliability, validity, and practicality. Actually, there are several major concepts in CTT. Chief among them are (i) the correction for attenuation, (ii) the Spearman-Brown formula, (iii) the reliability index, (iv) the Kuder-Richardson formulas, and (v) the Guttman's lower bounds to reliability. CTT was the product of the early 20th century. It was the result of three remarkable achievements of the past:

• A recognition of the presence of errors in measurement.
• A conception of that error as a random variable.
• A conception of correlation and how to index it.

In fact, Spearman's “correction for attenuation” marked the beginning of the classical test theory in 1910. CTT is based on the assumption that measurement error, which is a random latent variable, is a component of the observed score random variable. The main offshoots of CTT are (1) the ancillary assumptions invoked and experimental procedures followed in estimating coefficients of reliability, and (2) the standard errors of measurement.

As early as the 17th century Galileo had reasoned that errors of observation were distributed symmetrically and tended to cluster around their true value. By the beginning of the 19th century, astronomers had come to recognize errors in observation as an area worthy of research. Carl Friedrich Gauss, for example, derived what is known as normal distribution. At the beginning of 20th century, the idea of measurement error was unanimously accepted by all ranks of measurement specialists. It was at this time that the idea of correction of a correlation coefficient for attenuation came into play. Spearman, for example, had the foresight to realize that the absolute value of the coefficient of correlation between the measurements for any pair of variables must be smaller when the measurements for either or both variables are influenced by accidental variation than it would otherwise be. Out of these considerations came the idea of reliability.

Reliability is often defined as consistency of measurement. A reliable test score will be consistent across different characteristics of the testing situation. Reliability goes hand in hand with validity in that it is the prerequisite to validity. In other words, reliability and validity are considered to be complementary. That is, for a test to be valid, it must first be reliable. Whereas validity concerns language ability, reliability has to do with measurement and interpretation factors.

Proponents of CTT believed that a score made by a given subject on a given test is not necessarily an index of his/her ability. It is rather a combination of error score (i.e., random error variance) and true score (i.e., true variance or classical true score (CTS)). The important point is, therefore, to minimize the effects of measurement errors and to maximize the effects of language abilities to be measured. To this end, measures of test reliability were considered vital. According to Bachman (1990), any investigation of reliability might be based on either 'logical analyses' (which enable us to identify the sources of errors) or 'empirical research' (which can estimate the magnitude of the effects of errors on test performance). These considerations resulted in the birth of Classical True Score (CTS).

CTS was based on two assumptions: (a) An observed score is a function of both true and error scores; (b) Error scores are random in the sense that they do not correlate to true scores. It should be remembered that, in CTS models, there are only two sources of variance in scores: a single ability (usually called the true score variance), and a single error source (usually called the error score variance). The error score variance is normally considered to be unsystematic and random. Furthermore, the true score variance is the result of differences in ability levels of testees. Reliability is, therefore, expressed in CTS in terms of true score (TS) variance.

In general, there are three different reliability models in CTS: (i) Internal Consistency Estimates, (ii) Stability Estimates, and (iii) Equivalence Estimates. Internal consistency estimates determine the stability or consistency of test-takers' performance on different parts of a test. Stability measures, on the other hand, to determine if test-takers' performance remains consistent over time. And, equivalence estimates set out to determine if the same test-takers manifest the same performance characteristics on two 'parallel tests'. 'Parallel tests' is a CTS concept which refers to two or more highly correlated tests that show the same true score for an individual test-taker. The idea behind developing parallel tests is that the error variance of one equals the error variance of the other, and that the true score variance of one equals that of the other. Parallel tests may also be referred to as equivalent forms or alternate forms.

There are at least seven different methods of estimating the internal consistency of a test in CTS.

These methods include:

• split-half reliability.
• Spearman-Brown split-half estimate.
• the Guttman split-half estimate.
• Kuder-Richardson reliability coefficients.
• coefficient alpha.
• intra-rater reliability, also known as regrounding.
• inter-rater reliability.

The last two methods are sometimes referred to with the generic term 'rater consistency'. In split-half reliability, the correlation coefficient is calculated for two sets of scores acquired through breaking a single test into two halves. There are three different methods of assigning test items into the two halves: odd-even method, first-half-secondhalf method, and random-halves method. One point of caution, however, is that, no matter which of the three methods is used, the two halves must be both independent and equivalent.

After splitting the test into two halves, the scorer must rescore them so that he will come up with two different sets of scores. Since splitting reduces the total test length, it must be made up for either through Spearman-Brown prophecy formula, or through Guttman split-half estimate. The Spearman-Brown formula assumes that the two halves are both equivalent and experimentally independent. This is crucially important because nonequivalent halves result in the under-estimation, and nonindependent halves in the over-estimation, of reliability coefficients. Guttman's formula, however, does not assume equivalence of the two halves. Furthermore, it does not require the scorer to compute the correlation coefficient between the two halves since it is based on variance. Because of the same reason, it is possible to calculate the reliability of the whole test directly by means of Guttman's reliability estimate.

When dealing with split-half reliability, the scorer must keep in mind that reliability somehow depends on the method of splitting the test. To avoid this potential trap, the scorer must follow these steps: (i) use all the methods of splitting, then (ii) estimate the reliability coefficient for any of them, and then (iii) find the average of these coefficients. Another problem is that there are practically various ways of splitting a test into two halves. As such, the greater the number of items in a test, the greater the number of possible halves. To avoid this problem, testers are usually recommended to use the famous Kuder-Richardson formulas.

Internal consistency measures are based on only one test and one administration of that test. Some tests, however, do not lend themselves to measures of internal consistency simply because their parts are not independent of each other. There should, therefore, be alternate ways for measuring the reliability of these tests. One such method is 'test-retest reliability' defined as the re-administration of the same test with a time interval. The assumption behind test-retest is that test-takers do not change in any systematic way between the two administrations. Furthermore, test-retest reliability is on the horns of a dilemma: a long time interval between the two administrations results in a greater chance for “ability change” in test-takers, and, conversely, a short time interval results in a greater change for the 'practice effect' (also known as history effect or carry-over effect) to take place. This problem is best dispensed with through the use of equivalent or parallel test reliability.

Anyhow, measures of reliability based on CTS have been criticized on the following grounds:

• Sources of error might interact with each other;
• There are some sources of error which are by no means controllable;
• The estimation of the sources of error is relative;
• Errors are treated in a homogeneous way; and
• Errors are assumed to be random, not systematic.

Reliability has to do with the amount of variation in test scores due to test method facets, and measurement errors (both systematic and random). Validity, on the other hand, talks about the relationship between testperformance and other types of performance in other contexts. In a discussion of the role of validity in CTT, Farhady (1980) delineates three methods of determining test validity: (a) examining the content of the test and its correspondence to the content of the corpus to be tested (i.e., content validity), (b) examining the relationship between two tests claiming to measure the same ability (i.e., criterion related validity), and (c) examining the underlying structure of the test to investigate whether the test measures the predefined ability or not (i.e., construct validity).

Content validity means the extent to which the selection of tasks one observes in a test-taking situation is representative of the larger set or the universe of tasks of which the test is assumed to be a sample. In order to judge whether or not a test has content validity, one needs a specification of the skills or structures that the test is meant to cover. A comparison of test specifications and test content is the basis for judgements as to content validity. It should always be kept in mind that content validity guarantees the accuracy with which a test measures what it is expected to measure. Moreover, it safeguards the test against the influence of harmful backwash effect.

Another approach to test validity is to see how far results on the test agree with those provided by some independent and highly dependable assessment of the candidates' ability. Such a criterion-related measure of validity has two different manifestations: concurrent validity, and predictive validity. The former is established when the test and the criterion are administered at about the same time. The latter, however, is established when the test and the criterion are subsequent to each other. Predictive validity concerns the degree to which a test can predicate candidates' future performance.

Construct validity has to do with the correspondence between test content and the content of the predefined ability to be measured. A test, some part of it, or a testing technique has construct validity if it measures just the ability it is really expected to measure. “Construct” refers to any underlying ability or trait that is hypothesized in a theory of language ability. As such, construct validity is a research activity by means of which theories are put to the test and are confirmed, modified, or abandoned. It is through construct validation that language testing can be put on a sounder, more scientific footing.

A not-so-much-scientific concept in test validation is the notion of 'face' validity. A test is said to have face validity if it looks as if it measures what it is supposed to measure. Face validity is hardly a scientific concept; nevertheless, it is very important. A test that does not have face validity may not be accepted or taken seriously by candidates, educators, teachers, or other authorities concerned. The implication of face validity for testing is that novel techniques, particularly those that provide indirect measures, have to be introduced slowly, with care, and with convincing explanations.

In sum, CTT developed out of the observations made by scientists, mathematicians, and astronomers in relation to measurement errors. The basic idea behind CTT is that there is only one source of error in any instance of measurement. The coefficient of correlation is a powerful tool in interpretations of the findings of CTT. Proponents of CTT developed their own measures of reliability (i.e. internal consistency, stability, and equivalence estimates), and validity (i.e. content, criterion referenced, and construct). Face validity is a non-scientific addition to the concept of validation in CTT.

Out of the shortcomings of the classical test theory born a new measurement theory called Generalizability theory (or simply G-theory). The key figures who have helped GTheory forward as early as 1972 are Cronbach, Geleser, Nanda, and Rajaratnam. Their seminal work on G-Theory entitled “The dependability of behavioral measurements: Theory of generalizability for scores and profiles appeared in 1972.” Shavelson and Webb (1981) reviewed G-Theory from 1973-1980, and Shavelson, Webb, and Rowley (1989) provided a very brief overview of G-Theory.

In discussing the genesis of G-Theory, Cronbach (1951) argued that generalizability is actually the reinterpretation of reliability. To delineate G-Theory, Cronbach and his colleagues delivered a very rich conceptual framework and married it to the analysis of random effect variance components. It is not uncommon for G-Theory to be described as the application of analysis of variance (ANOVA) to CTT. Such a characterization is more misinformative than useful. Nevertheless it correctly suggests that the G-Theory parents can be viewed as CTT and ANOVA. Brennan (1984) eloquently argued that GTheory was not a replacement for CTT although it did liberalize the theory. Moreover, not all ANOVA is related to G-Theory.

Fisher's (1925) work on factorial designs gave impetus to the proponents of G-Theory to develop specific statistical machinery for G-Theory. G-Theory, however, emphasizes the estimation of random effect variance components. In this connection, it is noteworthy that, by 1950, there was a rich literature on reliability from the perspective of classical test theory. This literature and a wealth of other research on reliability formed the backdrop for G-Theory. Cronbach's argumentation (1984) that some type of multi-facet analysis was needed to resolve In consistencies in some estimates of reliability was perhaps the first leap forward towards the by-then quite mysterious notion of G-Theory. The 1950s were the years in which various researchers began to exploit the fact that ANOVA could handle multi-facets simultaneously. Lindquist (1953), for instance, laid an extensive exposition of multi-facet theory that focused on the estimation of variance components in reliability studies. He demonstrated that multi-facet analyses led to alternative definitions of error and reliability coefficients. These findings clearly foreshadowed important parts of GTheory. G-Theory requires that investigators define the condition of measurement of interest to them. The theory effectively disavows any notion of these being a correct set of conditions of measurement, but it is clear that the particular tasks or items are not a sufficient specification of a measurement procedure.

In 1951, Ebel, in an article on the reliability of ratings, concluded that error sources were twofold: (a) one that included rater main effects, and (b) one that excluded such effects. It was not until G-Theory was fully formulated that the issues Ebel grappled with were fully and truly clarified in the distinction between relative and absolute error for various designs. Along the same lines, Lord's (1957) proposal of the 'binomial error model' became an integral part of G-Theory. It is probably best known as a simple way to estimate conditional Standard Errors of Measurement (SEMs) and as an important precursor to strong true score theory. It was not until 1960-1961 that the essential features of univariate G-Theory were largely completed with technical reports. Studies on inter-battery reliability provided part of the motivation for the development of multivariate G-Theory.

The Cronbach, et al. (1972) formulation of G-Theory was general enough to allow for any set of conditions to be the objects of measurement facet. In a series of articles about the symmetry of G-Theory, Cardinet and his colleagues emphasized the role that facets other than persons might play as objects of measurement. Kane and Brennan (1980) report their being intrigued with the idea of using GTheory to address issues surrounding the reliability of criterion referenced (or domain referenced) scores. It was not until the late 1980s that interest in performance testing led to a mini-boom in Generalizability analyses and considerably greater publicity for G-Theory. In particular, practitioners of performance testing realized that understanding the results of a performance test necessitated grappling with two or more facets simultaneously (especially tasks and raters).

A comparison between Classical Test Theory and GTheory reveals that, unlike CTT which favored only one source of error, G-Theory draws on a universe of errors. According to G-Theory, the sources of measurement error include cultural content, psychological task set, topastic or guessing error, and so forth. Specifically, G-Theory holds that a given measure or score is a sample from a hypothetical universe of possible measures. In other words, a score is a multi-factorial concept. The implication of such a proposition is that, when interpreting a single test score, one can certainly generalize from a single measure to a universe of measures. For instance, one generalize from the test performance of a test-taker to his performance in other contexts. As such, reliability is a matter of Generalizability. Moreover, to be able to generalize, one must define their universe of measures.

There are two stages or phases in the use of G-Theory in language testing: G-study and D-study. G-study is the abbreviation for 'Generalizability study'. It has to do with studying the sources of variance. By contrast, D-study has to do with a decision study. D-study is the second phase of the implementation of G-Theory. As such, G-Theory is the administration of the test under operational (i.e., real test use) conditions as well as determining the magnitude of the sources of variance. In other words, G-Theory includes (i) specification of sources of variance, (ii) simultaneous identification of the magnitude of these sources, and (iii) implementation of these estimates to test interpretation and use. This latter phase is somehow directly related to validation.

It can safely be argued that Classical True Score (CTS) is an incomplete G-Theory. In CTS, there are only two sources of variance: (a) a single ability, and (b) a single error. In GTheory, there may be multiple sources of error. The universe of generalization concerns such domains as the 'uses', 'abilities', or 'both' to which any given test score is generalized. The G-universe has a number of characteristics that can be captured under two headings: (a) specific characteristics or facets, and (b) varying conditions in each of these facets. In any instance of the application of G-Theory, one should first define the universe of possible measures, and then define the population of persons. The key criterion in the definition of the population of persons is the degree of Generalizability we allow to a given testing situation. Population characteristics can be defined in terms of age, level of language ability, and characteristics of language use.

The universe score is different from CTS in that any given individual is likely to have different universe scores for different universes of measures. Furthermore, there is no such true score for all persons, times, and places. The Generalizability coefficient calculated in G-Theory is the analog to reliability index in CTS. Generalizability coefficient is the proportion of observed score variance that is universe score variance. The sources of variance in G-Theory are referred to as 'variance competence'. Perhaps one of the most interesting sources of variance in G-Theory is test-takers' heterogeneity. It is, however, noteworthy that variance components in G-Theory usually depend on the specific testing context.

According to G-Theory, there are three major sources of variance that envelop all other types of variance: (a) universe score variance, (b) systematic variance, and (c) random or residual variance. The major purpose of GTheory is, therefore, the systematic identification and the empirical examination of sources of variance simultaneously. G-Theory estimates for more than two sources of variance at the same time. It also provides comparable reliability estimates for tests of differing lengths with differing number of raters.

It is often stated that G-Theory 'blurs the distinction between reliability and validity'. Yet very little of the GTheory literature directly addresses validation issues. Kane's (1982) Sampling Model for Validity is a notable exception. It is clearly one of the major theoretical contributions to the literature on Generalizability theory in the past 25 years. Kane clearly begins to make explicit links between G-Theory and issues traditionally subsumed under validity.

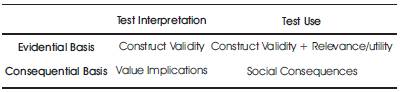
Validity is no longer viewed as a three-dimensional concept as it was explained in CTT. It is rather a unitary concept the nucleus of which is the famous notion of “construct validity” as proposed by Messick (1988). Stating that construct validity is the key concept in language testing, Messick views validity as an integration of complementary forms of convergence and discriminate evidence. Such a unified concept of validity is composed of six different aspects: (i) the content aspect, (ii) the substantive aspect, (iii) the structural aspect, (iv) the generalizability aspect, (v) the external aspect, and (vi) the consequential aspect. Table 1 illustrates these validity components.

Table1. Facets of Validity Envisaged by Samuel Messick (1988)

As indicated by Table 1, Messick's (1988) model of validity is a four-way framework based on a two-fold foundation: (i) an evidential basis, and (ii) a consequential basis. This foundation functions as the source of justification for the use of any measure. This four-way framework is appropriate for both test interpretation and test use. In other words, construct validation is at the heart of any attempt at test interpretation on an evidential basis. Relevance, utility, and construct validity should go hand in hand in the process of test use on an evidential basis. On a consequential basis, however, test interpretation draws on both construct validation and value implications. Last but not least is the consequential perspective in test use. To this end, an integrative model embracing relevance, construct validity, utility, and social consequences should be implemented. In other words, the validation process is based on both evidential and consequential bases, which in turn draw their concerns from content relevance, criterion relatedness, and construct meaningfulness. At the same time, validation entails both interpretation and use of tests.

In this perspective, validity is an integrated evaluative judgment of the degree to which “empirical evidence and theoretical rationales support the adequacy and appropriateness of inferences and attitudes based on test scores or other modes of assessment” (Messick, 1988, p. 13). Validity here, then, relates to the evidence available to support test interpretation and potential consequences of test use.

Item Response Theory (or aka IRT) is also sometimes called latent trait theory. As opposed to classical test theory, IRT is a modern test theory. It is not the only modern test theory, but it is the most popular one and is currently an area of active research. IRT is much intuitive approach to measurement once you get used to it. In IRT, the true score is defined on the latent trait of interest rather than on the test, as is the case in classical test theory. IRT is popular because it provides a theoretical justification for doing lots of things that classical test theory does not. Some applications where IRT is handy include:

IRT provides a test of item equivalence across groups. It is possible, for instance, to test whether an item is behaving differently for blacks and whites or for males and females. The same logic can be applied to translations of research tools (e.g., questionnaires) into different languages. It is possible to test whether the item on a given research instrument means the same thing in different languages—is culture-bound.

When a teacher has scores on one test and likes to know what the equivalent score would be on another test (e.g., versions or forms of the same test). IRT provides a theoretical justification for equating scores from one test to another.

IRT provides an estimate of the true score that is not based on the number of correct items. This frees the test-maker to give different people different test items but still place people on the same scale. One particularly exciting feature of tailored testing is the capability to give people test items that are matched (close) to them. A tailored testing program for proficiency, for example, will give more difficult items to brighter test takers. It also has implications for test security because, through tailored testing, different people can get different tests.

By the end of the last century onwards, the field of language testing continued to embrace the notion of performance assessment as a means of achieving a close link between the test situation and authentic language use. To this end, the relative directness of the relationship between test and criterion was (and still is) thought to enhance the validity of the inferences that we draw from our test data. However, we still need to provide additional evidence of reliability and validity for our assessment. In this connection, a lot of factors have been pinpointed to influence the chances of success for a candidate on a test. IRT models attempt to capture these factors and the impact they leave on the final outcome of tests.

A brief look at the trends in language testing presented above shows that the Generalizability Theory (or G-theory) extends the framework of CTT in order to take into account the multiple sources of variability that can have an effect on test scores. In other words, G-theory allows the investigator to decide which facets will be of relevance to the assessment context of interest. G-theory is expected to be able to all the various facets of a measurement procedure into account, and to differentiate their effects via the estimated variance components, on the dependability of decisions or interpretations made from the test scores. Furthermore, it is expected to allow us to estimate the change in our measurement procedures.

There are, however, some points that might not be simply captured by G-theory. Therefore, the Item Response Theory (IRT) models came into vogue to compensate for any shortcoming of the prevailing test theories. The use of IRT in the examination of the qualities of language tests is a comparatively recent development and one that has proved controversial. Drawing on the work of Rasch (1980), IRT has featured in a number of studies since the early 1980s. The basic Rasch model conceptualizes the expected performance of individuals on a test item or task as a function of their ability and the difficulty of the item. Many-facet Rasch measurement, however, makes it possible to include additional assessment variables, such as rater severity, whose effect is also taken into account in estimating the person's underlying ability.

Many-facet Rasch measurement also allows us to identify particular elements within a facet that are problematic, or misfitting. This may be a rater who is unsystematically inconsistent in his or her ratings, a task that is unsytematically difficult across the measurement observations, or a person whose responses appear inconsistent. Through a feature known as bias analysis, one can also identify specific combinations of facet elements (such as particular rater-task combinations) that are consistently different from the overall pattern identified in Rasch analysis, as well as combinations that are random in their deviation from that pattern.

Rasch IRT has sometimes been discussed primarily as a tool for improved investigation of the reliability of tests. Its potential for investigating aspects of validity of language tests has also been demonstrated. The application of IRT in this latter role has in some cases met with objections. These objections are based on what are claimed to be its unsatisfactory theoretical assumptions, and in particular the unidimensionality assumption—that is, (any) item/items in a test measure(s) a single or unidimensional ability or trait, and items form a unidimensioanl scale of measurement.

The assumptions upon which language testing models are based make them different. CTT, for instance, proves inadequate for predicting future performance of individuals for two reasons. On the one hand, the classical true score makes no assumptions about the interaction of an individual's ability-level and his test performance; on the other hand, item facility/difficulty (i.e., IF/D) is the only index of predicting an individual's performance on a given test. In other words, examinees' characteristics and test characteristics are so intertwined that a low IF index may equally be taken to indicate either that the test has been difficult or that the test takers were low-ability students. This implies that test results are sampledependent; it is difficult, if not impossible, to compare students who have taken different tests, or to compare items that have been tried out on different groups of students (Alderson, Claphan, and wall, 1995). IRT, on the other hand, assumes that an individual's performance on a test is based on (i) the ability level of that individual, and (ii) difficulty level of the item. In other words, IRT relates individual's test performance to their language ability levels.

Item Response Theory (IRT) draws on Item Characteristics Curves (ICCs). Since IRT is based on probability theory, a test taker has a 50/50 chance of getting an item right when that person's ability level is the same as that item's difficulty level. This indicates that, in IRT, students' scores and item totals are transformed on to one scale so that they can be related to each other. The relationship between examinees' item performance and the abilities underlying item performance is visually described in an Item Characteristics Curve (ICC). A typical ICC will look like the one displayed by Figure 1.

Figure1. The appearance of a typical ICC

An ICC (or item trace) can be analogized to an electrocardiogram (ECG), in medicine, by which a physician obtains a tracing of the electrical activity of the heart on a graph. An examination of the ECG can give the physician an idea of how the patient's heart is functioning. Here in IRT, too, an ICC can give the testing expert an idea of how a given test taker is performing on a test item. In much the same way as the functioning of the heart in an ECG is based on the patient's level of health, in an ICC, too, the performance of test-taker is controlled by his level of ability.

It is customary in IRT to talk about the latent trait as theta (q) or the logit scale ability. It is also customary to set the theta scale by considering the population mean equal to zero and the population standard deviation to one (i.e., as an analog to the normal probability curve values or traditional z-scores). Note that in the graph the center of the theta scale is zero and the numbers go up and down from there. Thus, 1 corresponds to 1 standard deviation above the mean and -1 to one standard deviation below the mean. For a vocabulary item, it stands to reason that the probability of getting the item right should increase as ability increases. The vertical axis is the probability of getting the item right.

ICCs are the cornerstones of IRT models. They express the assumed relationships between an individual's probability of passing an item and his level of ability. There are three basic parameters or characteristics in IRT:

• Item Discrimination or Discrimination Parameter, which is symbolized by a
• Item Facility/Difficulty, which is symbolized by b; and
• Topastic or guessing effect, which is symbolized by c.

In addition to these parameters, IRT also takes the ability scale (or the horizontal axis of the curve, known as theta and symbolized by θ) and the probability scale (or the vertical axis, symbolized by ρ or µ) into account. There is also a constant symbolized e for which the contant value is 02.71 mathemetically. The following equation shows the relationships between these IRT concepts:

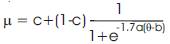
Item difficulty or the b parameter is the most important of these parameters. It sets the location of the inflection point of the curve. The b parameter sets the location of the curve on the horizontal axis; if, for example, the guessing or c parameter of a test is equal to zero, then the inflection point on the curve will be at µ = 0.50. The location of b can be found by dropping a vertical line from the inflection point to the horizontal axis. In the one-parameter IRT model (also known as the Rasch Model) only allows this parameter to vary to describe different items.

The item discrimination parameter or a-parameter has to do with the relationship between items and individuals' ability levels. The a parameter is the steepness of the curve at its steepest point. It is found by taking the slope of the line tangent to the ICC at b. Its closest relative in classical test theory is the item total correlation. The steeper the curve, the more discriminating the item is, and the greater its item total correlation. As the a parameter decreases, the curve gets flatter until there is virtually no change in probability across the ability continuum. Items with very low a values are pretty useless for distinguishing among people, just like items with very low item total correlations. The two-parameter IRT model allows both a and b parameters to vary to describe the items.

The c parameter is known as the guessing parameter. The c parameter is a lower asymptote. It is the low point of the curve as it moves to negative infinity on the horizontal axis. In essence, the c parameter is the topastic effect (also called Psudo-chance/guessing effect) that determines the probability of providing the correct answer to an item by a low-ability test-taker. One can think of c as the probability that a chicken would get the item right. The c parameter can, for example, be used to model guessing in multiple choice items.

In IRT, for each item an ICC is plotted. Depending on the exact IRT model used in plotting them, ICCs can present different pieces of information. By now, there are three famous IRT models: (i) the three-parameter model, (ii) the two-parameter model, and (iii) the one-parameter (Rasch) model. The three-parameter model takes all the three parameters of item discrimination, item facility/difficulty, and topastic effect into account. The two-parameter model only draws on item difficulty/facility, and item discrimination. By contrast, the one-parameter or Rasch model only takes the item facility parameter into account. These parameters are plotted in the form of curves on the basis of two scales: the X-axis represents the ability scale, and the Y-axis shows the probability scale. Hambleton and Swaminathan (1985) developed the notion of Ability Score on the basis of their IRT study. They collected a set of observed item responses from a large number of test-takers. They, then, fitted IRT models to the data and selected the best one. One the basis of the bestfitting IRT model, they assigned estimates to items and scores to individuals.

IRT is a leap forward towards guaranteeing the precision of measurement. There is the probability of running into the problem of imprecision of measurement in both CTT and G –theory estimations of SEM, reliability, and generalizability, simply because they are sampledependent. In other words, the same test finds different reliabilities for different groups of test-takers. Another source of imprecision in both CTT and G-theory is the fact that error variance is treated as homogeneous across individuals. In other words, estimates are groupdependent not individual-dependent.

Another important key issue in IRT is called Item Information Function (IIF). Item Information Function refers to the amount of information a given item provides for estimating an individual's level of ability. Item Information Function is based on two pedestals: ICC slope, and variation at each ability level. The sum of all Item Information Function's affords what is normally referred to as Test Information Function (TIF). Test Information Function (TIF) is an estimate of how much information a test provides at different ability levels. In other words, the SEM for each ability level is the reverse of Test Information Function (TIF) for that ability level. All these considerations guarantee that IRT measures are sample-independent; hence, measurement precision or reliability.

IRT models have been criticized on the grounds that they are not that much applicable to the estimation of validity indices. The basic problem to IRT models by now is its unidimensional assumption—that there is a single latent trait; the application of IRT in determining test validity has in some cases met with objections based on what are claimed to be its unsatisfactory theoretical assumptions. It, therefore, remains an important future endeavor for testing and measurement specialists to work on this aspect of IRT theory to enhance it to the status of a comprehensive and exhaustive theory of measurement.

A recent development of IRT is Differential Item Functioning (DIF). DIF analysis is a procedure used to determine if test questions are fair and appropriate for assessing the knowledge of various ethnic groups and females. It is based on the assumption that test takers who have similar knowledge (based on total test scores) should perform in similar ways on individual test questions regardless of their sex, race, or ethnicity (Zumbo, 1999).

DIF occurs when people from different groups (commonly gender or ethnicity) with the same latent trait (the same ability/skill) have a different probability of giving a certain response to an item. DIF analysis provides an indication of unexpected behavior by item on a test. An item doesn't display DIF if people from different groups have a different probability to give a certain response; it displays DIF if people from different groups in spite of their same underlying true ability have a different probability to give a certain response.

In essence, DIF analysis is very much similar to G-theory in the sense that it identifies sources of systematic variance other than true variance; due to their systematic nature, they may present constant measurement error which may be mistakenly seen as part of true score as was the case in CTT. DIF analysis has not fully blossomed in language testing practice yet. There is a lot of opportunity for language testing specialists to work in this field.

In this paper, it was noted that the field of language testing, there have been four major trends until now: the Classical Test Theory (CTT), with its notion of Classical True Score (CTS) and Random Error; the Generalizability Theory (G-Theory), with its notion of universe score being composed of true, systematic, and random variance sources; Item Response Theory (IRT), with its notions of Latent Trait, Parameters, and Probability; and Differential Item Functioning (DIF), with its identification of sources of systematic variance other than the latent variable of interest.

It should be noted that the material presented above is not the sole property of language testing. Any testing practice, in any field ranging from hard sciences such as mathematics and physics to soft sciences such as literature, can benefit from this paper. The testing models presented in this paper can be safely applied to all instances of educational measurement.