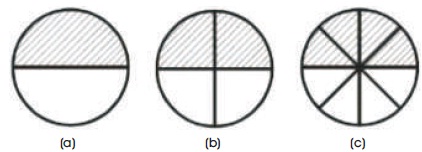
Figure 1. Fraction according to Circle Representation divided into Congruent Parts and with the Same Size
Pirie & Kieren (1994b) states that conceptual understanding in human beings is divided into eight levels. This qualitative and descriptive research study aims to identify the layers of conceptual understanding of fractions through three representations, namely of circles, rectangles, and number lines. The subjects of this research are three sixth-grade students from SD Batu Malang. The instruments of this research are an essay test consisting of 12 questions and a semistructured interview. The essay test is adopted from Tunç-Pekkan (2015) and test the fractional analysis of a circle representation, rectangle-representation, and number line representation with four questions provided for each representation. The data analysis of this research uses the resource triangulation technique. Based on the work done by the students, the results show that in terms of layers of conceptual understanding, Subject 1 demonstrated understanding layers from Primitive Knowing (Pk) through Property Noticing (Pn), Subject 2 demonstrated understanding layers from Image Making (Im) through Property Noticing (Pn); and Subject 3 demonstrated understanding layers from Image Making (Im) through Formalizing (F).
Mathematics is an abstract system consisting of various structures and correlations and includes consecutive abstractions and generalization processes (Yilmaz, Özdemir, & Yasar, 2018). The study of mathematics involves several subjects, one of which is fractions. Kurniawan et al. (2016) said that definition of fraction can be categorized into two meanings, namely 1) as quantity expressed relative amount and 2) as a number that has an emblem. The National Mathematics Advisory Panel in 2008 concluded that conceptual understanding of fractions and fluency in using procedures to solve problems related to fractions are central goals of mathematical development (Bailey, Hoard, Nugent, & Geary, 2012). Fractional of analysis is an abstract concept that students often have difficulty understanding (Yilmaz, Özdemir, & Yasar, 2018). Many efforts have been undertaken to introduce the concept of fractions to elementary school students through various representations. There are at least three representations that can be used to introduce the concept of fractions; these include the circle, rectangle, and number line. Fractions are often represented by a circle that is divided into several parts that are congruent in both shape and size, as depicted below.
The number fraction shown in Figure 1 illustrate that:
Figure 1(a) shows the fraction of 1/2; Figure 1(b) shows fraction of 2/4; and Figure 1( c) shows fraction of 4/8. The relation shown from the illustration is 1/2=2/4=4/8. In this case, the numerator is shown by the amount of shaded parts of the circle and the denominator is shown by the amount of the rest of the circle parts which is congruent and at the same size.

Figure 1. Fraction according to Circle Representation divided into Congruent Parts and with the Same Size
The fractional concept analogy can also be represented with a rectangle that is divided into several congruent parts of the same size.
The fraction shown in Figure 2(a) illustrate fraction of 1/2; Figure 2(b) illustrate fraction of 2/4; and Figure 2( c) illustrate fraction of 4/8. The relation shown from the illustration is 1/2=2/4=4/8.
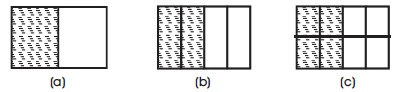
Figure 2. Fraction through Rectangle Representation that is divided into the Same Size and Congruent
In this case, the numerator is equal to the number of shaded rectangle parts and the denominator is equal to the total number of the rectangle's parts, all of which are congruent and of equal size.
Fractions can also be represented by a number line, as shown below.
Fraction shown in Figure 3 illustrate that:
Figure 3(a) illustrate fraction of 1/2; Figure 3(b) illustrate fraction of 2/4; and Figure 3( c) illustrate fraction of 4/8. The relation shown from the illustration is 1/2=2/4=4/8.
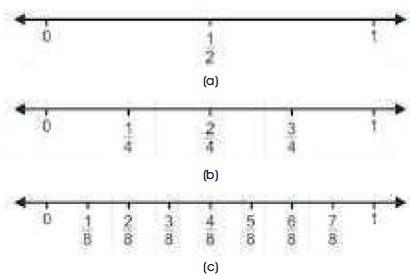
Figure 3. Fraction from Number Line Representation
The principle that is used to introduce the fraction concept through number line representation is the number located in between the two integers in sequence, which are fraction or decimal number.
The three representations (circle, rectangle, and number line) can be used to introduce the concept of fractions to elementary students. They are very helpful to the students' understanding of the concept.
Fauziyyah and Kriswandani (2017), and Pirie and Kieren (1994b) state that understanding is composed of eight levels or layers: Primitive Knowing (Pk), Image Making (Im), Image Having (Ih), Property Noticing (Pn), Formalizing (F), Observing (O), Structuring (S), and Inventing (Iv). This theory states that understanding is not always linear and continuous. People often return to previous layers of understanding before advancing to more advanced levels of understanding. These layers are depicted in Figure 4.
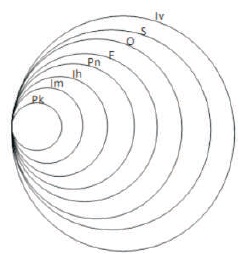
Figure 4. Pirie and Kieren's Levels of Development of Understanding Mathematics
Figure 4 illustrates the layer model of understanding. The first layer, Primitive Knowing, is the first effort made by students and involves understanding the most basic definitions before building additional layers of understanding which involve those definitions. The second layer of understanding, Image Making, is the stage where students create an understanding of previous knowledge and use it as their initial knowledge on material studied to produce new knowledge in that material. The third layer of understanding, Image Having, is the stage where students already have an idea of the material being studied and create an abstract picture of the subject without having to work on examples. The fourth layer, Property Noticing, is the stage where students are able to combine the concepts of a topic to establish specific properties of that topic. The fifth layer of understanding is Formalizing, and in this stage students create abstractions and visualize a mathematical concept based on the properties that appear, forming a definition of the concept in the process. The sixth layer of understanding is Observing. In this layer, students are able to use the concepts that have been connected to the material so that they can associate their understanding of mathematical concepts with new knowledge structures. In the seventh layer of understanding, Structuring, students are able to use the understanding they have constructed to form links between theorems and prove those theorems with logical arguments. Students are also able to prove the connections between theorems axiomatically. The eighth layer of understanding is Inventing, and in this last layer, the students have formed a complete structured understanding that they did not previously possess and are able to create new questions concerning the problems or materials they are learning (Pirie & Kieren, 1994a; Susiswo, 2014; Sagala, 2016; Syahri & Isran, 2016; Utami & Rosyidi, 2016; Fauziyyah & Kriswandani, 2017). Therefore, this research aims to identify the layers of conceptual understanding through students' analyses of circle, rectangle, and number line representations.
This research is a qualitative descriptive study. The subjects in this study were chosen using purposive sampling techniques. Three sixth-grade students were selected from an elementary school in Batu, Malang in East Java, Indonesia. The students had been studying fractions since the fourth grade. The instrument used in this research consisted of the main instruments and supporting instruments. The main instrument was the researchers, while the supporting instrument was an essay test consisting of 12 questions about fractions, as well as guidelines for the interview. The essay test was adopted from Tunç-Pekkan (2015) and included four questions about analyzing fractions based on circle representations (Figure 5(a), 5(b), 5( c), and 5(d)), four questions about analyzing fractions based on rectangle representations (Figure 6(a), 6(b), 6( c), and 6(d)), and four questions about analyzing fractions based on number line representations (Figure 7(a), 7(b), 7( c), and 7(d)).
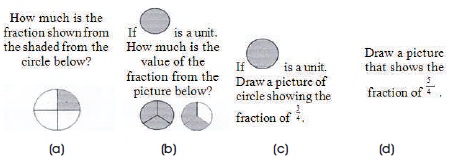
Figure 5. Fraction Question through Circle Representation

Figure 6. Fraction Question through Rectangle Representation
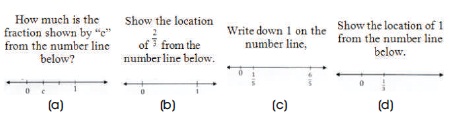
Figure 7. Fraction Question through Number Line Representation
The data collection techniques in this research consisted of observation, testing, and in-depth interviews. The data analysis techniques in this research included data reduction, data presentation, and conclusion.
The layers of conceptual understanding of the elementary students in learning fractions based on circle, rectangle, and number line representations are shown in the following subsections.
The answers of Subject 1 in analyzing fractions through circle and rectangle representations are shown in Figures 8 and 9.
According to the answers of Subject 1 in Figures 8(a), 8(b), and 9(a), it can be seen that Subject 1 used the Image Making (Im) layer through the Property Noticing (Pn) layer. This means that Subject 1 understood the concept of the fraction based on the circle and rectangle representations. The shaded parts of the circle and the rectangle represent the numerator, and the total of all the parts represents the denominator. Therefore, Subject 1 recognized that the circle was divided into four congruent parts and the rectangle into five congruent parts and was therefore able to identify the denominators. Then, Subject 1 calculated the number of shaded parts of the circle and rectangle to identify the numerators. For example, according to the answer in Figure 8(a), Subject 1 answered, explaining that there were four parts of the circle and only one part that was shaded. This shows that Subject 1 understood the concept of fractions based on the circle and rectangle representations and applied it to the questions given. For Figures 8( c) and 9(b), Subject 1 provided answers of three fourths and five sixths, respectively, for the representations of the circle and rectangle. The first thing the subject did was to make a circle and rectangle and then divide them into four and six parts of equal size. In this case, Subject 1 could not represent the fraction correctly in terms of size. After that, the subject shaded three parts of the circle and five parts of the rectangle. It shows that Subject 1 used the Image Having (Ih) layer.
According to Figure 9(c), Subject 1 put five rectangles in a parallel and separate orientation. In fact, Subject 1 should have made one big rectangle, divided it into five parts of equal size, and then shaded only one part of the rectangle. The size of the rectangle is determined by the question given. It shows that Subject 1 used the understanding layers of Primitive Knowing (Pk) followed by Image Making (Im). Next, in Figures 8(d) and 9(d), it can be seen that Subject 1 analyzed the fractions based on circle and rectangle representations using the layers of Image Making (Im) through Image Having (Ih) and Property Noticing (Pn). This means that Subject 1 used the conceptual knowledge of fractions and integers through the circle and rectangle representations in order to illustrate the fraction of one fourth. For Figures 8(d) and 9(d), Subject 1 represented the problem using two circles and two rectangles. One circle and rectangle were fully shaded, while the other circle and rectangle were divided into four parts of equal size with only one part shaded on each. The circle and rectangle had the same representation for described fraction number.
Subject 1's answers in analyzing the fraction based on a number line representation are shown in Figure 10.
Based on Figure 10, Subject 1 used the Ih and Ph layers. This means that Subject 1 used the identification of specific characteristics in the number line to identify numbers on the number line and then determined the number being asked in the questions. Regarding the specific characteristics in Figure 10(a), according to Subject 1, there were three parts, of which c was the first part, so the subject answered one third in Figure 10(b). The subject then looked at the question and directly divided the number line into three points and gave notations of those points on Figures 10( c) and 10(d). Subject 1 directly identified the first numbers in sequence. From this identification of specific characteristics, Subject 1 continued by answering the questions given and then depicted the location of the number on each number line. Subject 1 was not able to make the number line correctly because of the different distances for each number.
The answers of Subject 2 in analyzing fractions based on the circle and rectangle representations are shown in Figures 11 and 12.
Based on the answers of Subject 2 for Figures 11(a), 11b), and 12(a), it can be seen that Subject 2 used the Im layer through the Pn layer. This means that Subject 2 understood the fractions based on the circle and rectangle representations. Subject 2 was not sure on Figure 12(a), so the subject determined the fraction to be either one fifth or four fifths. Finally, the subject determined the fraction to be one fifth and supported the answer by stating that the rectangle was divided into five parts with one part shaded. Based on the answers given in Figures 11( c) and 12(b), Subject 2 represented fractions of three fourths and five sixths based on the circle and rectangle shapes. First, the subject made a circle and rectangle and divided them into four parts and six parts, respectively. The component parts of the shapes were nearly congruent and more accurate than the figures of Subject 1. Then, the subject shaded three parts of the circle and five parts of the rectangle. The subject explained that each part of the circle was divided into four parts representing fourths and each box representing one fourth. Therefore, Subject 2 made the overall representations of a circle and rectangle, divided them into four and six congruent parts, determined the size of each part, and then shaded the parts. This shows that Subject 1 used the Imagine having (Ih) layer.
Based on Figure 12( c), Subject 2 made a rectangle, which was divided into five parts that were almost equal in size. Then, the subject shaded all of the parts and explained that each small rectangle represented one fifth of the overall shape. This shows that Subject 2 analyzed fractions based on the circle and rectangle representations by using the layers of Im through Ih and Pn. Subject 2 used knowledge of mixed fractions and integers to analyze the circle and rectangle representations and identify the fraction of five fifths. For Figure 11(d), the subject represented the problem with two circles, where one complete circle was fully shaded and another circle was divided into four parts, where one part was shaded. For the representation of the rectangle, Subject 2 drew two rectangles, with each rectangle divided into four parts of equal size. The first rectangle was fully shaded and the second rectangle was partly shaded. Both the representations had different meanings. The fully shaded circle represented a whole unit and was notated as 1, while the circle that was divided into four parts and partly shaded was notated as a fraction. In order to represent the fraction of one and one fourth, two circles and two rectangles were needed, where the first circle and rectangle were divided into four parts and fully shaded to show the integer of 1, and the second circle and rectangle were divided into four parts with just one part shaded.
The answers of Subject 2 in analyzing fractions based on the number line representation are shown in Figure 13.
Based on Figure 13, the ability of Subject 2 in drawing the number line was better and more systematic than Subject 1. To analyze fractions through the representation of number line representation, Subject 2 used the Ih and Pn layers. It means that Subject 2 analyzed the number line by finding the information known from the question and then made filled out the number line. Subject 2 made the number line with a complete notation distance. The subject also understood that between two integers in a sequence, there were fractions. For example in Figure 13(b), Subject 2 wrote “1” and instead of three thirds not and also explained the position of other fractions.
The answers of Subject 3 in analyzing fractions through based on the circle and rectangle representations are shown in Figures 14 and 15.
Based on the answers of Subject 3 in Figures 14(a), 14(b) and 15(a), it can be seen that Subject 3 used the layers of Ih through Pn. In analyzing the fractions given, Subject 3 consistently represented them through circles and rectangles starting from the overall shapes and then dividing them into the fractions given in the question. In Figure 14(a), Subject 3 described the fraction of one and one fourth through the representation of a circle that was divided into four parts and fully shaded to notate the integer 1, and then made the same circle, but only shaded one part and it to depict the fraction of one fourth. Thus, Subject 3 always began the representation by representing or referring to integers. Based on the student's answers in Figures 14( c) and 15(b), Subject 3 represented the fractions as circles and rectangles and began by shading the overall parts of the circle and rectangle representations. Subject 3 always began the representation for integers first, followed by fractions. For example, in Figure 15(b), the fraction one and five sixths was represented by two rectangles divided equally into six parts. The first rectangle was divided into six parts and fully shaded, and this was notated as integer 1. Then, the second rectangle was divided into six parts with five of its six parts shaded. The subject notated the overall fraction as one and five sixths. This shows that Subject 3 used the Ih and Pn layers.
Figure 15. The Answers of Subject 3 in Analyzing Fractions through based on a Rectangle Representation
Based on Figure 15(c), Subject 3 defined that the fraction had denominator of 5. Therefore, one whole unit was composed of five smaller rectangles. The subject did not determine the representation of the numerator and therefore only arranged five rectangles in a sequence. This shows that Subject 3 used the Im layer. Then, in Figures 14(d) and 15(d), it can be seen that Subject 3 analyzed fractions through the circle and rectangle representation by using the Im, Ih, and Formalizing (F) layers. Subject 3 used knowledge of mixed fractions by adding the integers with the fractions. Subject 3 determined the fraction in Figure 15(d) to be five fourths. Subject 3 analyzed Figures 14(d) and 15(d) through the circle and rectangle representations. The circle representation was a circle divided into four parts and fully shaded, representing the integer 1, then the subject added to it one shaded part of the second circle and notated the overall number as one and one fourth. For the rectangle representation, the subject drew a rectangle divided into four parts and notated this as four fourths, then the subject combined it with one part of the second rectangle and notated the overall fraction as five fourths. To represent the rectangle, Subject 3 did not use shading.
The answers of Subject 3 in analyzing fractions based on the number line representation are shown in Figure 16.
Based on Figure 16, the ability of Subject 3 was as good as the ability of Subject 2 in making a number line. To analyze fractions through the representation of the number line, Subject 3 used the Ih and Pn layers. This means that Subject 3 analyzed the number lines by finding information known from the question and then filling out the number lines completely. After that, Subject 3 determined the position of the number presented in the question. For example, in Figure 16( c), Subject 3 drew number line, then drew a box marking the position of the integer 1 and explained that because the denominators were all equal to 5, the number 1 would be obtained on the point of five fifths.
The layers of conceptual understanding used by the three students in representing fractions based on the circle, rectangle, and number line representations are summarized in Table 1.
Table 1. The Layers of Conceptual Understanding of Fractions based on Circle, Rectangle, and Number Line Representations for Sixth-Grade Elementary Students
A person's layer of conceptual understanding is not static but dynamic and is always transitioning from one level to another. Sometimes, a person's layer of conceptual understanding move on before layer of conceptual understanding and then move on next layer of conceptual understanding. This transition is very dynamic and this process is called folding back. In this case, it can be said that fold backs, which are similar to types that students studied at a more inner layer by using their current understandings are effective in students' understanding levels (Sengul & Argat, 2015). This corresponds to the research done by Sagala (2016), Susiswo (2014), Utami and Rosyidi (2016), and Fauziyyah and Kriswandani (2017). These transitions enable students to effect changes in their understanding of concepts.
Fractions are one of the more difficult subjects for students to understand and present a significant potential for misconception. This is supported by the research done by Karaoglan Yilmaz et al. (2018), who stated that fractions are one of the most extensive and difficult subjects of mathematics teaching programs (Yilmaz et al., 2018). Particularly during primary school, when the teaching of fractions is initiated after the teaching of natural numbers, the difficulties of teachers to instruct increase rapidly, and this situation affects students' success and can negatively impact students' development. When the related literature is examined, it can be seen that many students have learning difficulties and misconceptions about fractions. One of the main reasons for learning difficulties in the teaching of fractions is the prevalence of misconceptions on the subject. The relevant misconceptions about fractions stated in the literature can be summarized as follows: 1) showing fractions on the number line; 2) sorting, summation, and multiplication operations with fractions; 3) dividing a number by zero, dividing zero by a number, and the relationship between integers and rational numbers; and 4) the part-to-whole relationship. To minimalize this misconception, we must identify student's understanding especially fraction before we design the mathematics learning.
Identification layer of conceptual understanding with Pirie-Kieren Theory guides for observing and defining the process thoroughly in which knowledge is structured through repetitive organizations and about the perceptions of students, how they think and how they structure their thoughts with a suitable way (Sengul & Argat, 2015). With this reasoning, teacher can design mathematics learning which can be understood by the student quickly and appropriately. Finally, student's layer of conceptual understanding has transition dynamicaly and develop to higher layer of conceptual understanding.
Layer of conceptual understanding based on Pirie-Kieren Theory can related with APOS (Actions, Processes, Objects, Schemas) based on Dubinsky Theory. Actions similar with primitive knowing and image making, processes similar with image having property noticing, objects similar with formalizing and observing, and schemas similar with structuring and inventing (Sagala, 2017). An action is a transformation of objects perceived by the individual. If the action is related with layer of conceptual, students can create their initial knowledge that involves understanding the basic definition and creating an understanding of previous knowledge. The second, when an action is repeated and the individual reflects upon it, he makes an internal mental construction. If process is related with layer of conceptual, students can have an idea and create an abstract picture and then they are able to combine the concepts to establish specific properties of a material. The third, an object will be formed when the individual becomes aware of the process as a totality and realizes that transformations can act on it. If an object is related with layer of conceptual, students can associate their understanding of mathematical concepts with new knowledge structures based on the properties of abstractions, visualize a mathematical concept, and forming a definition of the concept. The fourth, a schemas is combination of actions, processes, objects, and other schemas. If a schema is related with layer of conceptual understanding, students are able to use the understanding they have constructed to form links between theorems and prove those theorems with logical arguments. Futhermore, the students have formed a complete structured understanding that they did not previously possess and are able to create new questions concerning the problems or materials they are learning.
The layers of conceptual understanding of fractions based on circle, rectangle, and number line representations for the sixth-grade elementary students in Batu, Malang are summarized as follows: Subject 1 used the understanding layers of Primitive Knowing (Pk) through Property Noticing (Pn), Subject 2 used the layers of Image Making (Im) through Property Noticing (Pn), and Subject 3 used the layers of Image Making (Im) through Formalizing (F). To provide a more detailed explanation, the layers of conceptual understanding based on the circle and rectangle representations for Subject 1 were Im and Pn, for Subject 2 were Im and Pn, and for Subject 3 were Ih and Pn. The ability of Subjects 1 and 2 to represent fractions as circles and rectangles demonstrated the Ih understanding layer, while Subject 3 used the Ih and Pn understanding layers. To represent rectangles as fractions and then represent them as rectangles again, Subject 1 used the Pk and Im understanding layers, Subject 2 used the Ih understanding layer, and Subject 3 used the Im understanding layer. For the ability to form the representations of a circle and rectangle in understanding fractions, Subjects 1 and 2 used the Ih and Pn understanding layers, and Subject 3 used the Im, Ih, and F understanding layers. The understanding layers of fractions through the representation of number lines for all three subjects were Ih and Pn.
Insights that the statistics education community badly needs to have, even though it may not know it yet. I would like to thank all these wonderful people and my family. I hope my article is useful for knowledge developing, especially about layers of understanding. To develop sudent's layers of understanding, teacher must design the qualify learning so the layers of understanding increases actively.