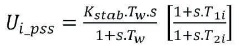
In this paper, the multi-machine Power System Stabilizer (PSS) with Genetic Algorithm (GA), PID-PSS using GA and PID-PSS using Ant Colony Optimization (ACO) have been proposed. The aim of designing a robust controller is to improve transient stability and damping of low frequency oscillations. The conventional PSS is replaced by PID-PSS and a research has been done on feedback controllers design using artificial intelligence optimization techniques that are GA-PSS, GAPID- PSS and ACO-PID to obtain the best performance of transient stability control of multi machine power system. The minimization criteria of error overshoot and settling time is done through Integral of Time-weighted Absolute Error (ITAE) method. The research found that GA-PID-PSS has better performance over GA-PSS, such that tuning of PID-PSS is again resolved through ACO based metaheuristic technique. This ACO-PID-PSS is coordinated with Static VAR Compensator (SVC) with a Proportional Integral (PI) type auxiliary controller. The proposed coordination is tested in a 4 machine 6 bus power system in MATLAB/Simulink. The robustness and impressiveness of the proposed coordination results were compared with their overshoot and settling time.
In the current scenario, the electric power system has become a large interconnected electrical network, so regular and effective power supply is very necessary to provide stabilized electricity to the distribution networks. Stability is most important term in electrical power system. Stability is influenced by the nonlinear characteristics of power system (Singh et al., 2019). Stability aims to maintain the voltage and frequency levels under all disturbances like transients, interruptions, overloads, loss of any generator, sag and swell or voltage fluctuations on any interconnected transmission line causing a fault. Weak interconnection in the power system causes low frequency oscillation (0.2-3 Hz). These oscillations require proper and early damping to enhance the system stability. The Power System Stabilizer (PSS) is equipped with each generator to provide damping to the electromechanical oscillation. The main purpose to install PSS is to provide low frequency rotor oscillation damping by excitation control of generator using auxiliary stabilizing signals i.e., acceleration power, frequency deviation and speed deviation (Kundur et al., 1994).
Recent research papers introduce the replacement of Conventional Power System Stabilizer (CPSS) through Proportional Integral Derivative (PID) controller (Jariwala & Chowdhury, 2012) or by introducing the coordination of PID+PSS (Kasilingam & Pasupuleti, 2015) to improve the small signal effectively and transient stability. Apart from PSS and PID controllers, the Flexible AC Transmission System (FACTS) devices are coordinated to enhance the transient stability (Fu et al., 2012). Especially, in multi machine systems, the CPSS provides sufficient damping for local oscillation (1-3 Hz), but not for inter-area oscillation (0.2-0.5 Hz), so the coordination of FACTS devices with PSS introduces effective damping and improvement on transient stability (Linda & Nair, 2012). The PID-PSS controller analysis with Bat algorithm on single machine infinite bus has been done by Chaib et al. (2017). This particular analysis has been done to minimize the error, overshoot and settling time on single machine system.
The damping improvement of multi machine system is not the main purpose of FACTS device; this is one of its applications. The primary function of FACTS devices is to enhance the control capacity and increase power transfer ability (Shakarian et al., 2019); basically it controls the frequency and voltage levels under their respective criteria. The FACTS devices include SVC, STATCOM, TCSC and UPFC has led their application to damp out inter-area oscillation (Hingorani et al., 2000).
The objective of this paper is to analyse the transient stability enhancement of power system and to evaluate the best solution through different controller and their coordination. CPSS is replaced by GA-PSS and then GAPID. The investigation of best solution is continued by using evolution an Evolutionary Algorithm (EP) a generic population-based meta heuristic optimization algorithm entitled as Ant Colony Optimization PID-PSS (ACO-PID-PSS). After that, to minimize undershoot, overshoot and damping; the FACTS device SVC is coordinated at the middle of transmission line. The proposed scheme is tested in 4 machines and 6 buses test system in MATLAB.
Commonly, the excitation controller is applied to maintain the equilibrium between magnetic and electric torques in the machines. The excitation systems allow controlling the speed and consequently the active power.
1.1.1 Power System Stabilizer (PSS)
The PSS is an essential part of the excitation system, whose function is to control the excitation by adding damping to the rotor oscillations of the generator. The primary application of PSS is to generate an electric torque on the rotor of the synchronous machine, which is required to maintain the steady state behavior. PSS is a feedback controller, which is employed to damp out the small frequency oscillations of the limit of 0.1-2.5 Hz. The multi-machine power system stabilizer transfer function for ith PSS is given in equation (1).
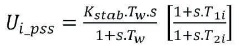
where, Kstab, Tw and Tii represents stabilizer gain, wash time constant and compensator time constants respectively. Figure 1 endows the block diagram of a tentative conventional lead-lag PSS (Singh et al., 2016b). It is acknowledged that in the PSS design, the high pass (washout) filter time constant Tw and the upper and lower limits of the PSS output signals V(stab_Max) and V(stab_Min) respectively are prespecified values and the stabilizer gain Kstab and the phase lead-lag time constant T1, T2, T3, and T4 are the parameters to be designed.
1.1.2 Proportional Integral Derivative PSS (PID-PSS) Controller
Proportional Integral Derivative (PID) is a feedback controller technique used for responsive correctness in error e(t). PID works for minimum delay and low overshoot. PID controller gives robust performance based on the selection of its three parameters, which are Proportional gain (Kp), Integral gain (Ki), and Derivative gain (Kd). Robust means the controller provides wide control on system during undesired and unexpected conditions like high loading, external disturbances, faults, size and locations of machine etc. (Mahdavian et al., 2016). PID calculation involves the selection of three parameters: Kp, Ki, and Kd, because PID does not guaranty the optimal control if selection of parameters are not proper, in such cases traditional methods or intelligent optimization techniques are used to tune the PID factors.
SVC is a basic FACTS device, primarily used for shunt compensation to maintain bus voltage and frequency under the specific range. SVC regulates the bus voltages by automatic and frequent control of reactive power loading. SVC uses the thyristors for switching purpose, the firing angle (α) of these thyristors are regulated through a Proportional-Integral (PI) controller (Keskes et al., 2017). The SVC susceptance (Bsvc) is the function of firing angle α.
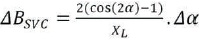
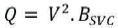
where, Q is reactive power and V is bus voltage. The block diagram of a PI type SVC is shown in Figure 2. The reason behind using SVC is analyzing the effect and performance of a very basic FACTS device on stability of the test system.
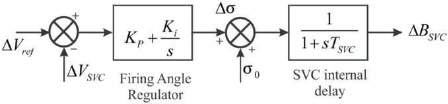
Figure 2. Block Diagram of PI Type SVC Controller
GA is a search algorithm depends on the mathematics of intrinsic selection and natural genetics. The theory of GA was first presented by Holland in the function of advancement and adaptation in intrinsic and artificial systems (Singh et al., 2016a). It is based on the “survival of the fittest” concept (Darwinian Theory). Only the fittest will survive and reproduce and recreate, successive generation will become better and better. Evolution is optimizing process; each generation of breed is like iteration in numerical methods (Meena & Kumar, 2015). GA is a popular global optimization algorithm, which is an efficient optimization technique and requires a minimum parametrization.
To obtain the optimal controller, gains and factors of control system parameters are regulated to improvise the accuracy and minimize the error in each generation. To generate the optimal parameters of control system, the GA technique and ACO optimization is applied. To get better performance index and minimum delay, the function Integral of Time-weighted Absolute Error (ITAE) method is used. The objective function of the system is given in equation (4).
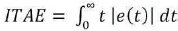
where, t represents the time and e(t) represents differences between desired value and measured value of controlled parameter. This criterion is based on error calculation in different process models (Xue et al., 2007). The primary application of ITAE method is to obtain the good performance index in designing the controllers like PSS and PID-PSS.
ACO is one of the best algorithms; it can be used widely in any field. The principle of ACO was presented by Marco Dorigo in 1992. It was real ant based algorithm, so it was first known as Ant system. The motivation of the ACO comes from stigmergy. By stigmergy, we mean that the mechanism of attraction and coordination between natural organisms or agents by modifying the next generation on environment. Stigmergy is a form of selforganization. It is metaheuristic based algorithm, which is inspired from foraging behavior of the species of the ants that leaves chemicals during food searching called pheromones (Dorigo & Stützle, 2019). The concentration of this pheromone is a pointer of the utility of that particular route to build better probability of the path between their nest and food. Ant colony algorithm is iterative. At every iteration, quantities of arrangements are consisted gradually based on stochastic choices that are biased by pheromone and heuristic data. The flow chart of the Ant Colony Optimization is shown in Figure 3. The ants starts to find the random or local solutions by initializing the ACO parameter. All ants visit through all cities and based on the maximum intensity of pheromone (i.e. maximum probability) ant follows the least distance path i.e., optimum length. The stopping criterion of ACO is depends on the number of iterations. The formula for getting the probability of choosing a random path by ants to move from the nest (one point-i) to food (another point-j) is given in equation (5).
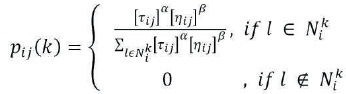
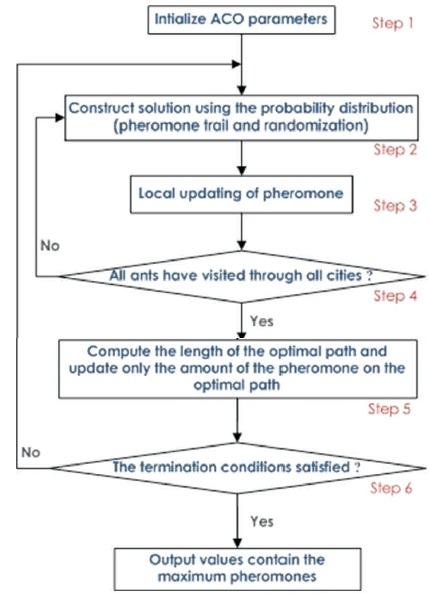
Figure 3. Flow Chart Diagram of ACO
where, and N is the neighbourhood of Ant k when it ith is at the ith point. The neighbourhood of i point implies all the nodes that are directly linked to it, excluding the pre-existing point. This ascertains the unidirectional transaction of the ants. The pheromone level is updated on every generation, which is given by an equation (6).
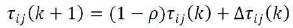
Here 0≤ρ<1 and ρ presents the evaporation rates of pheromone, and ∇τij is subjected to the performances of every ants and ∇τij(k) is given by,
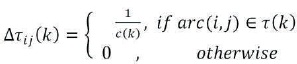
Here, c(k) is the length of the path found by kth ant. From all the feasible solutions, the algorithm selects the best ant cost to provide the least error based on ITAE objective function (4). The values of parameters used at the time of optimization are given in Table 1.

Table 1. Parameters of Ant Colony Optimization
In Table 1,α and β are the parameters which can increase or decrease pheromone level (τ) and ρ represents evaporation level in atmosphere.
The performance of the proposed PID-PSS controller tuned through Ant Colony Optimization (ACO-PID-PSS) and SVC controller is tested on simulated multi machine network. Single line diagram of test system having 4 machine and 6 buses is shown in Figure 4. All the 4 generators are equipped through a selector switch by which we can choose CPSS, PID-PSS or No PSS any one of them. The loads 1-5 are constant impedances; the values of loads are given in Table 2.
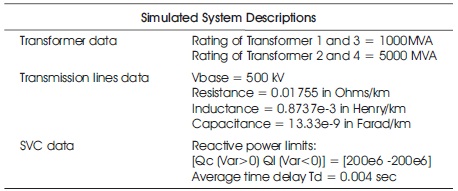
Table 2. Simulated System Descriptions
The feedback controller CPSS and PID-PSS are designed through Genetic Algorithm (GA) by connecting with objective function. GA is available in optimtool in MATLAB software. Then ACO technique is applied on PID-PSS and the coding is written to extricate the objective function.
4.1.1 PSS Design through GA
The conventional lead-lag PSS parameters are optimized value to provide the best performance of the system. GA is used for optimization. The optimized parameters are Kstab_i, T1i and T2i where i = 1, 2, 3 and 4. The best optimized values of CPSS are given in Table 3 and the fitness graph through GA is shown in Figure 5.
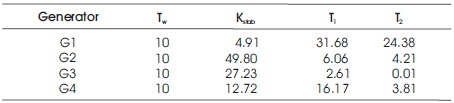
Table 3. Parameters of GA-PSS (Conventional PSS Parameters Optimized Through Genetic Algorithm)
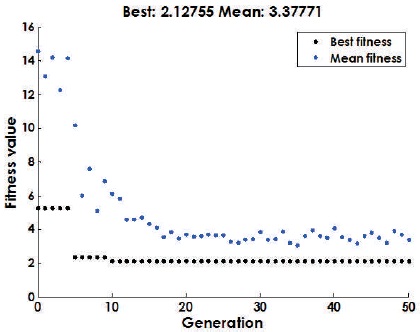
Figure 5. Genetic Algorithm Fitness Graph for PSS
4.1.2 PID-PSS Design through GA
The feedback controller PID-PSS parameters are Kp_i, Ki_i, Kd_i, where i (present in each parameter) =1 to 4. The GA based final optimized value of PID-PSS parameters are given in Table 4 and the fitness graph through GA is shown in Figure 6.
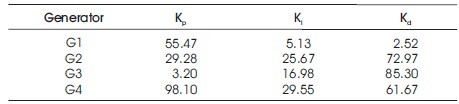
Table 4. Optimized Parameters of Ant Colony Optimization
4.1.3 ACO-PID-PSS Design
To demonstrate the robustness of PID-PSS parameters are optimized through Ant Colony Optimization. The objective function and optimized parameters are identical as GAPID- PSS. By comparing the performances obtained through both optimization, it is found that the best mean and effectiveness are better obtained by ACO-PID-PSS parameters. And it is also analyzed that ACO provides faster generations compare to GA. The supreme optimized values are given in Table 5 and the convergence graph of ACO is shown in Figure 7.
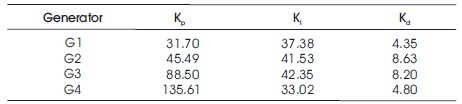
Table 5. Optimized Parameters of Ant Colony Optimization PID-PSS for Test System
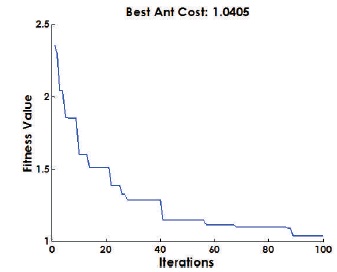
Figure 7. Ant Colony Optimization Convergence Graph for PID-PSS
To demonstrate the effectiveness and robustness of the proposed multifarious controllers are analyzed in following considerations:
4.2.1 Single Phase Fault-Impact with Different Controllers
A short-term single phase to ground fault is introduced at t = 0.1s and eliminated at t = 0.2 s using fault breaker. The test system equipped and turns with different feedback controllers, at this moment the SVC is operated in fixed susceptance mode (BSVC = 0), which represents SVC is out of service. After obtaining performance with proposed ACO-PID-PSS the SVC is operated in voltage regulation mode (BSVC = variable) to activate the SVC and analyze the performance coordinating controllers. The trace of rotor angle is shown combined for various controllers in Figure 8. And the comparison of peak time, peak value, overshoot and settling time is given in Table 6.
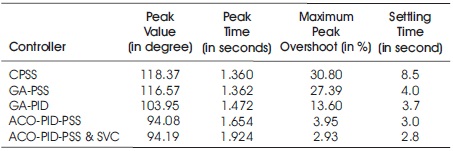
Table 6. Single Phase Fault Analysis. GA: Genetic Algorithm, PSS: Power System Stabilizer, ACO: Ant Colony Optimization
4.2.2 Three Phase Fault-Impact with Different Controllers
In another consideration the fault breaker is set to three phase fault, it is applied at t = 0.1 s and cleared at t = 0.2 s. The analyzing procedure has been continued same as single phase fault analysis, the simulated system is tested with multifarious controllers and SVC is attached as complimentary controller and operated through fixed susceptance and voltage regulation mode to inactivate and activate the SVC, respectively. The output trace of rotor angle for each controller is shown in Figure 9. The comparison analysis for three phase fault i.e. peak time, peak value, overshoot and settling time is given in Table 7 and the best mean from different optimization techniques are provided in Table 8.
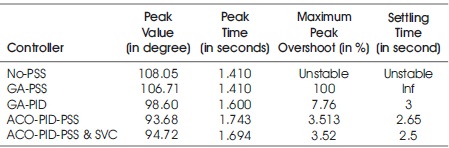
Table 7. Three Phase Fault Analysis. GA: Genetic Algorithm, PSS: Power System Stabilizer, ACO: Ant Colony Optimization, inf: infinite

Table 8. Best Mean from Different Controllers and Techniques
The paper shows the modern ACO based PID-PSS feedback controller for power system transient stability improvement and optimized robust PID-PSS is coordinated with basic FACTS device SVC to provide stable performance of the system. The parameters of CPSS and PID-PSS are optimized through GA and their performances were compared. Comparison of both shows that the GA-PID-PSS provides better outcome compared to GA-PSS. Thus, PID-PSS parameters are selected for ACO optimization. It is found from research that ACO iterations are faster than GA iterations and ACO provides better optimum values than GA.