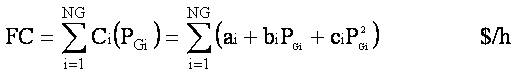
The modern power system analysis, operation and control use pneumatic solution methodologies to solve more realistic power system problems to enhance the operational aspects of power systems. The conventional load flow methods work independent of economic and environmental aspects and allocates total power losses to slack bus which increases the burden on this generator. In this paper, a novel methodology to remove extra generation by the slack and to optimize the system operation in economic and environmental aspects is presented. Further, a new hybrid optimization algorithm namely Improved Kinetic Gas Molecules Optimization (IKGMO) is presented to solve Optimal Power Flow (OPF) problem while satisfying system equality and inequality constraints. The effectiveness of optimization over the conventional load flow in loss allocation is tested on standard IEEE-14 bus and IEEE-30 bus test systems with supporting numerical and graphical results.
In a load flow study, real and reactive power cannot be fixed prior at all the buses as the net complex power flow into the network is not known in advance, the system power loss being unknown till the load flow study is complete. It is therefore necessary to have slack bus so that it supplies the difference in the total system load plus losses and the sum of the complex powers specified at the remaining buses. Hence slack bus must be a generator bus with maximum active power generation. In a power system, power flow equations are nonlinear and must be solved by iterative techniques. From this, it is motivated that, it is necessary to remove extra burden on slack bus. The literature [16, 17] presents a methodology to distribution of generation based on the frequency deviation. This method works based on automatic generation control using frequency characteristics. In [20], another technique based on NR load flow method was presented. In this method, loss term was introduced. In [1, 9, 11], the slack burden is removed in consideration with losses in economic aspect is presented. However, these methods suffer from the highest computational calculations and increased mathematical complexity.
Modern power system effective planning and reliable operation needs optimal power flow problem solution. The main objective of optimal power flow problem is to optimize the considered objectives related to the power system under certain system constraints. From the past few decades, most of the researchers have developed several classical techniques which have certain drawbacks regarding convergence rate and it is difficult to get local optima. Recently, some heuristic and metaheuristic Optimal Power Flow (OPF) algorithms have been developed and are efficiently applied to power system to solve power flow problems. Serhat Duman, et al., proposed gravitational search algorithm to solve OPF problem to find the optimal settings of control variables [6]. Wael T. Elsayed and Ehab, proposed a decentralized approach for the economic dispatch problems with non convex formulation [8]. Leandro dos Santos Coelho et al, described DE with truncated levy flight random walk with mutation operation and cross over operators to avoid premature convergence [5]. Yongsheng Zhu, et al., solved economic emission dispatch problem with Multiobjective case considering wind power using evolutionary algorithm based on decomposition principle [23]. M. Basu proposed modified PSO technique with guassian variables in updating the velocity of the partical and has proven that which improves search efficiency [3]. Sumit Banerjee, et al., presented a novel approach teaching learning based optimization to determine the optimal power generation while meeting the load and economic cost criteria [2].
After careful review of the literature, it is identified that, most of the literature is concentrated to minimize generation cost and very few concentrated to minimize emission. As the generator has both economic and emission characteristics, approximated using quadratic curve. Hence it is motivated that, the burden on slack bus can be released not only in economic aspect, but also in emission aspect. In this paper, an Optimal Power Flow (OPF) methodology is presented to minimize generation fuel cost and emission objectives while satisfying system equality and inequality constraints. After minimizing these objectives, the obtained power losses are further distributed to generators based on their cost and emission characteristics using slack distribution algorithm. As the conventional optimization algorithms are suffering from premature convergence and increased computational time, in this paper a new optimization algorithm, namely Improved Kinetic Gas Molecules Optimization (IKGMO) is presented to solve OPF problem. The complete methodology is tested on IEEE-14 bus and IEEE-30 bus test systems with supporting numerical and graphical results.
In modern power systems, the transmission losses were beared by the slack bus, so by using distributed slack bus we can remove the concentrated burden on the slack bus by distributing losses to each generator bus in the power system. This results in the system adjusting their outputs appropriately subject to their operational limits in order to achieve economic generation.
To distribute the burden on the slack bus among other voltage bus, a constraint named 'participation factor' is introduced into the existing ELD method [10]. A participation factor is a simple algebraic ratio. It is the factor attached to each generator bus such that the total uncounted or loss power shall be distributed to the bus multiplied by that factor. The sum of the participation factors is unity. The detailed derivation for the participation factor in economic and emission aspects is as follows:
The objective function is to minimize the overall cost of production of power generation. Let us consider 'NG' is the total number of units in the system and 'Ci(PGi)' is assumed to be the cost of power generation of unit-i, which is given for each plant. The total generation fuel cost (FC) objective function is defined as,
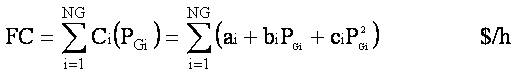
where, ai, bi, ci are the fuel cost coefficients of ith unit.
The economic power system operation needs to satisfy the following equality constraints.
Without losses: 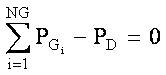
With losses: 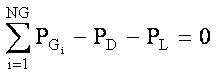
By considering the above constrained optimization problem along with the equality constraint can be solved by using the Lagrangian multiplier (λ). Then, the augmented fuel cost function becomes,
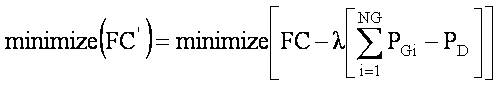
The condition for optimality of this augmented function is
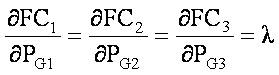
After solving equation (3) using equation (2), we get the necessary conditions for optimal dispatch when losses are neglected is as follows:
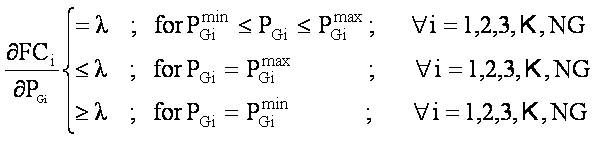
After solving equation (4) using equation (1), we get,
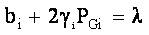
From this condition,
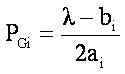
By applying summation on both sides for considering all generators and upon solving,
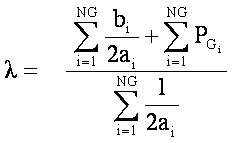
To remove extra burden on slack bus, the PGi including power losses can be calculated using equations (6) and (7).
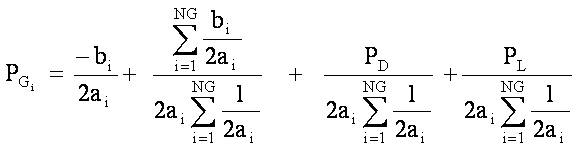
In equation (8), the first three terms refers to scheduled generation, hence, the new generation becomes,
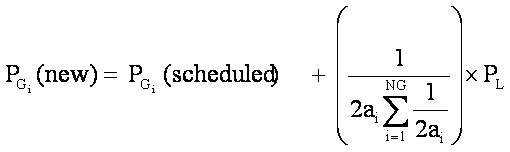
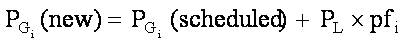
where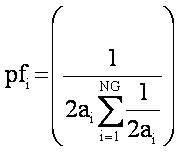 is called as loss contribution factor (participation factor) for cost minimization criteria.
is called as loss contribution factor (participation factor) for cost minimization criteria.
The objective function is to minimize the overall emission because of production of power generation. Let us consider 'Ei(PGi )' is assumed to be the emission of power generation of unit-i, which is given for each plant. The total emission (EC) objective function is defined as,
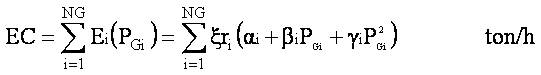
where, αi , βi , γi , ξi , ri are the emission coefficients of ith unit. The environmental concern of power system operation needs to satisfy the following equality constraints.
Without losses: 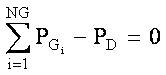
With losses: 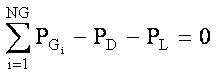
By considering the above constraints, optimization problem along with the equality constraint can be solved by using the Lagrangian multiplier (λ). Then, the augmented emission function becomes,

The condition for optimality of this augmented function is
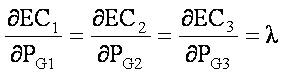
After solving equation (12) using equation (11), we get the necessary conditions for optimal dispatch when losses are neglected is as follows:
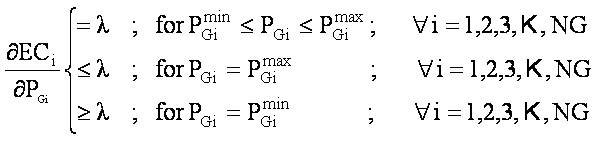
After solving equation (13) using equation (10), we get,
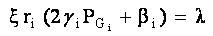
From this condition,
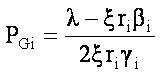
By applying summation on both sides for considering all generators and upon solving,
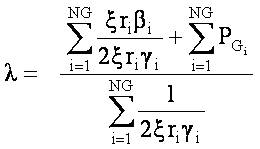
To remove extra burden on slack bus, the PGi including power losses can be calculated using equations (15) and (16).
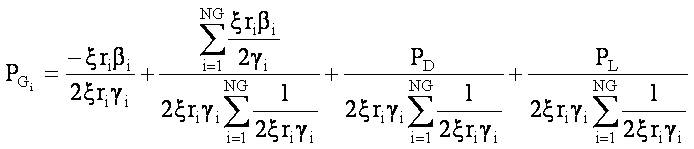
In equation (17), the first three terms refer to scheduled generation, hence, the new generation becomes,
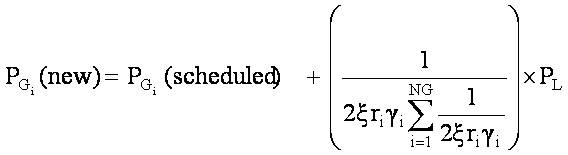
where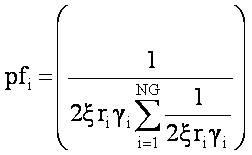 is called as loss contribution factor (participation factor) for emission minimization criteria.
is called as loss contribution factor (participation factor) for emission minimization criteria.
The flowchart for the modified load dispatch problem in economic and environmental aspects is shown in Figure 1.
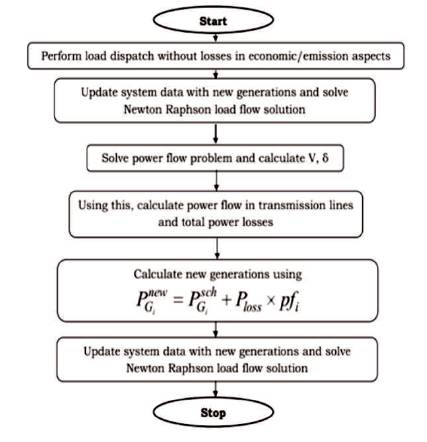
Figure 1. Flowchart for the Modified Load Dispatch Problem in Economic and Emission Aspects
The conventional optimization problem is formulated to identify an optimal set of control parameters to minimize any power system objective. In this process, the optimization procedure must satisfy the system equality and inequality constraints. The mathematical representation of the OPF problem can be formulated as,
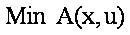
Subjected to,
g ( x,u ) =0 ; equality constraints and h (x,u ) ≤ 0; inequality constraints.
where, 'x' is a set of dependent parameters such as active power generation at slack bus (Pg, slack ) reactive power generation at generator buses (Qg ), power flow in the transmission lines (Sline ) voltage magnitude at load buses line (V). Similarly, 'u' is a set of independent parameters such as active power generation and voltage magnitude at generator buses (Pg , Vg ), transformer and shunt compensators settings (T, Qsh ).
The vectors of dependent and independent parameters can be mathematically expressed as,
Dependent parameters :
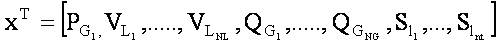
Independent parameters:
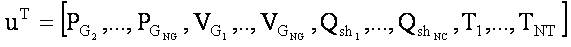
where, NL, NG, nl, NC, and NT are the total number of load buses, generators, transmission lines, shunt compensators, and tap changing transformers, respectively.
This OPF problem is solved using heuristic optimization technique (Improved Kinetic Gas Molecules Optimization) developed in section 3, while satisfying the following constraints.
The general power balance equations that are satisfied in conventional load flow solution can be represented for
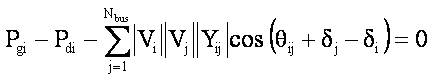
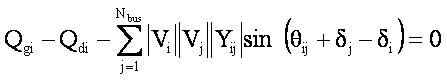
where, Pgi , Qgi and Pdi , Qdi are the active and reactive power generations and loads at ith bus, Vi , Vj and δi, δj are the voltage magnitudes and angles at ith and jth buses. Yij , θij are the magnitude and angles of the admittance of a transmission line connected between buses i and j, respectively. Here, Nbus is the total number of buses.
The following inequality constraints related to generators, security, OUPFC and other settings are considered in this work.
Active power generation limits:
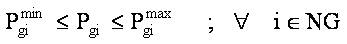
Reactive power generation limits:
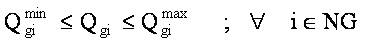
Generator voltage magnitude limits:
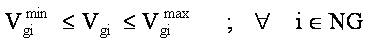
Transmission line MVA limit:
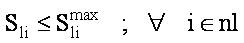
Load bus voltage magnitude limits:

Tap setting limits of the transformer:
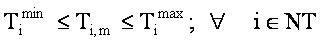
Shunt compensator MVAr limits:
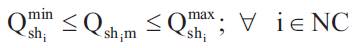
While solving OPF problem, independent parameters are not forced to violate their operating limits, whereas, dependent parameters are non-self restricted. These dependent parameters are handled using penalty approach. For this, the penalty functions related to slack bus active power generation, generators reactive power generations, load bus voltage magnitudes and transmission line MVA limits are added to the objective function [19]. The modified augmented objective function can be formulated as,
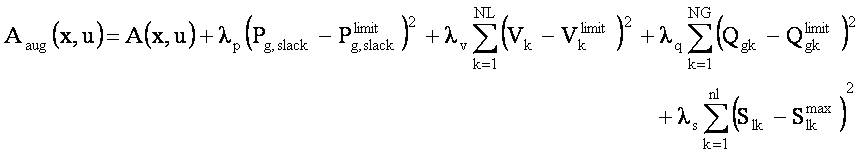
where, λp , λv , λq and λs are the penalty coefficients having large positive value and limit value can be defined as,

Here, 'n' is the value of Pg, slack , V, and Qg .
Sara Moein, and Rajasvaran Logeswaran [13] introduced Kinetic Gas Molecules Optimization (KGMO) based on the properties of gas molecules. In this algorithm, gas molecules considered as agents are tried to move in a container until they reaches the position where the temperature and kinetic energy are minimum. Gas molecules move in a container based on volume of the container, mass, velocity, Kinetic energy acquired by the gas molecules. In KGMO, each gas molecule updates their position in a multi dimensional search space. Each gas molecule moves towards the optimum point based on the updated velocity.
In general, for a given optimization problem and for a given number of population (K), the control variables and their velocities are generated between their minimum and maximum limits using the following expression.
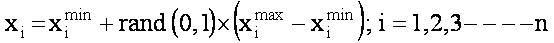
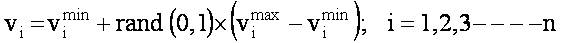
where, 'n' is the total number of control variables, Ximax, Ximin and Vimax , Vimin are the minimum and maximum limits of the control variables and velocities, respectively. For an electrical problem, the control vector generated for a given population can be represented as,
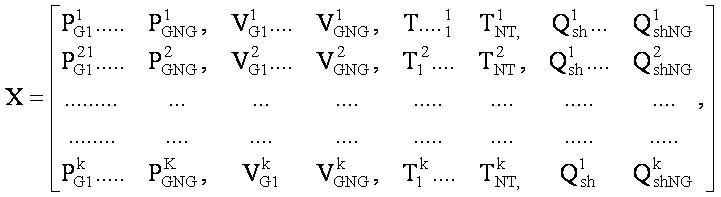
For each of the population, the fitness function is calculated using,
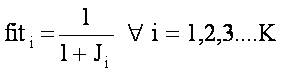
After evaluating fitness and objective function values (Pbest ), identify the global best function value (gbest ). Using these local and global best values, the updated velocity in (t+1)th iteration for ith control parameters in kth population can be calculated as,
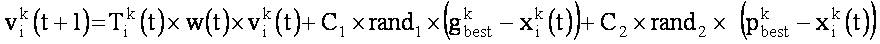
Here,
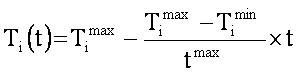 is the temperature, and this value linearly varies from 0.95 to 0.1.
is the temperature, and this value linearly varies from 0.95 to 0.1.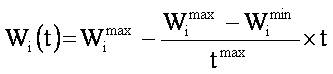 is the inertia weight, and this value linearly varies from 0.9 to 0.4.
is the inertia weight, and this value linearly varies from 0.9 to 0.4.vi (t) xi (t) are the velocity and positions of the ith control parameter in kth iteration, respectively.
C1 ,C2 and rand1 , rand2 are the acceleration coefficients and random numbers generated between 0 and 1, respectively.
The new position of the control variables can be calculated as,
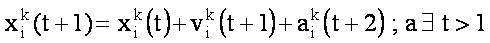
where 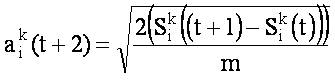
here 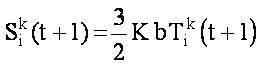
where, 'b' is the Boltzmann constant, 'm' is the random number between 0 and 1 and this value is fixed throughout the iterative process.
The performance of existing KGMO algorithm is improved by calculating acceleration coefficients and inertia weight dynamically rather than a constant value. Due to this, the searching capability of the particles in each of the iterations is improved.
These coefficients improve the search efficiency of the particles with increased velocity in searching the global best solution and with decreased velocity in searching the local best solution [14]. The dynamical acceleration coefficients can be calculated as,
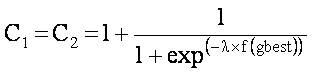
Here,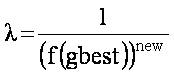
The weight factor is introduced to regulate the impact of previous velocity on the present velocity [7]. In each of the iterations, this factor is calculated as,
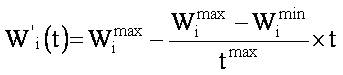
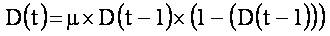
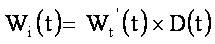
Here, 'μ' is a control parameter taken between 0 and 4. 'D' is a chaotic parameter changes as per the iteration number.
After evaluating the dynamic acceleration coefficients and inertia weight, a new modification is implemented to update the position of the gas molecules. In early iterations, the gas molecules are far away from the optimum solution in a search space with large radius. Due to this, the particles require more number of iterations to reach global best solution since then also the particles may not be able to reach global solution. Hence, the particles need the solution search space with small radius. For this, the dynamically varying search radius can be calculated as,
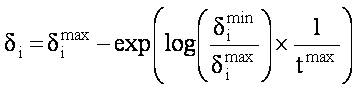
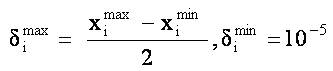
The new position of the gas molecules is calculated as,
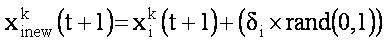
This new position improves the effectiveness of the particles in searching the global best rather than local best.
The flowchart of the developed IKGMO algorithm is shown in Figure 2.
At first, the total power losses are calculated using load flow formulation and these losses are then distributed to the generators based on their participation factors (Slack distribution algorithm explained in sections 1.1 for economic aspect and 1.2 for emission aspect). In this formulation, the constraints on dependent variables are not considered. In this paper, the generation fuel cost and emission objectives are optimized using developed IKGMO algorithm while satisfying system equality and inequality constraints. Finally, after minimizing these objectives, obtained losses are then distributed to the generators based on their participation factors respectively.
Step 1 : Solve OPF problem with generation fuel cost/emission as objective.
Step 2 : Evaluate total power losses.
Step 3 : Calculate participation factors (equation (9) in economic aspect and equation (18) in emission aspect).
Step 4 : Calculate new generations by distributing power losses to the scheduled generations as in section 1.
To show the effectiveness of economic and environmental aspects for slack distribution algorithm, in this paper, two test systems, namely IEEE-14 bus [18] and IEEE-30 bus [4] test systems are considered. The entire analysis is performed for the following two cases.
Case-1: Comparison of load dispatch results for economic and emission aspects.
Case-2: Comparison of loss distribution results obtained using OPF without and with slack distribution methodology for economic and emission aspects with NRLF.
For IEEE-14 bus system, the generator fuel cost and emission coefficients are given in Table 1. From these tables it is identified that, the generators connected at buses 1 and 3 has same fuel cost and emission characteristics. In general, bus-1 is the slack bus which supplies the total power losses plus the additional load which the existing generators have not supplied; this can be treated as extra burden on slack bus. In this paper, due to similar cost and emission characteristics, the generators connected at buses 1 and 3 must generate same amount to reduce extra burden on slack bus. For this, the procedure explained in section 3.2 is followed to remove burden on slack bus in economic aspect and in section 3.3 is followed to remove burden on slack bus in emission aspect.
At first, the load dispatch problem without losses is solved and scheduled generations (PGsch) are obtained in economic aspect, and then load flow problem is solved to get the total power losses. After that, these losses are distributed to all generators and new generations (PGnew) are calculated based on the procedure explained in section 1.1 in economic aspect and section 1.2 in emission aspects. The obtained numerical results are tabulated in Table 2. From this table, it is observed that, because of distribution of losses, the generation of the existing generators has been increased when compared to without distribution of losses, which in turn increases total generation. It is also observed that, because of distribution of losses, the total power losses are decreased when compared to conventional NR load flow.
From this table, it is also identified that, the generations are rescheduled to minimize the respective objectives. It is also observed that, while minimizing one of the objectives, the value of the other objective is increased. For example, while minimizing the generation fuel cost, the value of the emission is increased, this in turn increases the total generation and thereby the total power losses and vice-versa. The variation of generations in economic and emission aspects for without and with slack distribution is shown in Figure 3. From this figure, it is observed that, with slack distribution, the generation value of generators is increased when compared to without slack distribution. Similarly, the variation of generations without and with slack distribution in economic and emission aspects is shown in Figure 4. From this figure, it is observed that, while minimizing emission, thermal generators have decreased its generation due to highest emission coefficients, and Gas generators have increased its generation due to least emission coefficients when compared to cost minimization.
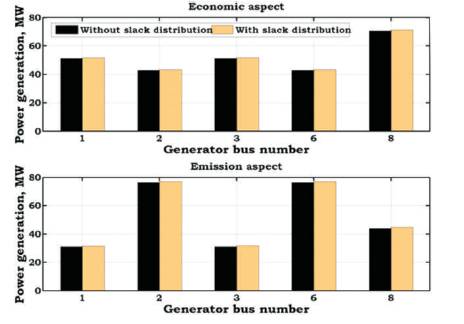
Figure 3. Variation of Generations in Economic and Emission Aspects with Slack Distribution for IEEE-14 Bus System
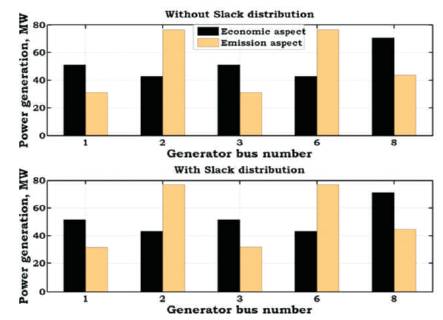
Figure 4. Variation of Generations without and with Slack Distribution in Economic and Emission Aspects for IEEE-14 Bus System
For Case-2, the OPF results with generation fuel cost and emission as objectives using KGMO and IKGMO are tabulated in Table 3. From this table, it is observed that, the proposed method yields better results when compared to existing method. The convergence characteristics are shown in Figures 5 and 6. From these figures, it is noticed that, IKGMO starts the iterative process with good initial value and reaches final best value in less number of iterations when compared to existing KGMO. This in turn decreases the computational time to get best value.
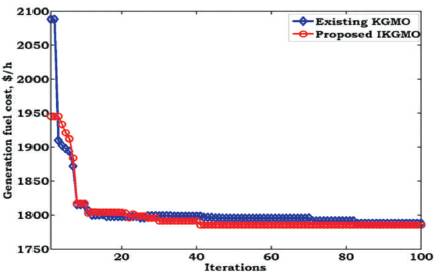
Figure 5. Convergence Characteristics of Cost Minimization for IEEE-14 Bus System
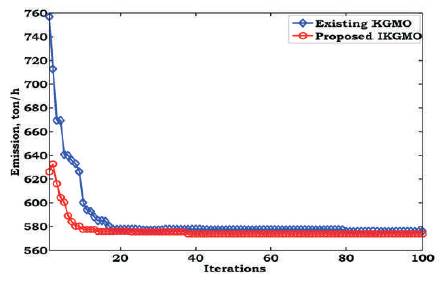
Figure 6. Convergence Characteristics of Emission Minimization for IEEE-14 Bus System
Further, the generation cost obtained with the proposed IKGMO is compared with the existing literature methods in Table 4. From this table, it is identified that, the proposed method yields less cost when compared to existing methods. Further in this work, the OPF problem is solved using IKGMO algorithm only.
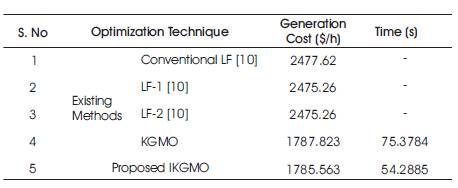
Table 4. Comparison of Literature Methods of Cost Minimization for IEEE-14 Bus System
After minimizing cost, obtained total power losses are distributed losses to all generators in economic aspect by following the procedure given in section 1.1. Using this, obtained results are tabulated in Table 5. From this table, it is observed that, in OPF, due to imposition of inequality constraints on dependent control parameters, the values of the total generation, generation fuel cost, emission and total power losses are increased when compared to NRLF. Because of rescheduling of generations in OPF and distribution of losses, the generation fuel cost is increased by 125.007 $/h when compared to load flow. It is also observed that, in OPF, the generator connected at bus-8 decreases it's generation drastically when compared to load flow, because of highest fuel cost coefficients.
Similarly, after minimizing emission, obtained total power losses are distributed losses to all generators in emission aspect by following the procedure given in section 1.2. Using this, obtained results are tabulated in Table 6. From this table, it is observed that, in OPF, due to imposition of inequality constraints on dependent control parameters, the values of the total generation, generation fuel cost, emission and total power losses are increased when compared to NRLF. Because of rescheduling of generations in OPF and distribution of losses, the emission is increased by 53.4975 ton/h when compared to load flow. It is also observed that, in OPF, the generators connected at buses-6 and 8 have decreased its generation drastically when compared to load flow, because of highest emission coefficients.
To show the effect of OPF over the load flow, the variations of generations using NRLF and OPF in economic and emission aspects are shown in Figures 7 and 8. From these figures, it is identified that, depending on the fuel cost and emission coefficients of the generators, the generations are rescheduled. It is also observed that, while minimizing generation cost, the generators with highest fuel coefficients decreased its generation and lowest fuel cost coefficients increased its generation. These type of generations variations are observed while minimizing emission also.
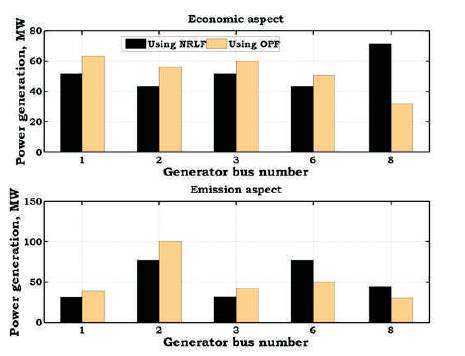
Figure 7. Variation of Generations using OPF in Economic and Emission Aspects for IEEE-14 Bus System

Figure 8. Variation of Generations in Economic and Emission Aspects using NRLF and OPF for IEEE-14 Bus System
For IEEE-30 bus system, the generator fuel cost and emission coefficients are given in Table 7. From these tables it is identified that, the generators connected at buses 1, 5 and 2, 8 have same fuel cost and emission characteristics, respectively. Hence, the generators connected at buses 1 and 5 must generate same amount to reduce extra burden on slack bus. For this, the procedure explained in section 1.1 is followed to remove burden on slack bus in economic aspect and in section 1.2 is followed to remove burden on slack bus in emission aspect.
Similar procedure as explained in example-1 is followed to distribute total power losses to generators based on their cost and emission coefficients, respectively to remove extra burden on slack bus. The obtained results are tabulated in Table 8.
From this table, it is also identified that, the generations are rescheduled to minimize the respective objectives. It is also observed that, while minimizing one of the objectives, the value of the other objective is increased. For example, while minimizing the generation fuel cost, the value of the emission is increased, this in turn increases the total generation and thereby the total power losses and vice-versa.
For Case-2, the OPF results with generation fuel cost and emission as objectives using KGMO and IKGMO are tabulated in Table 9. From this table, it is observed that, the proposed method yields better results when compared to the existing method.
Further, the generation cost and emission obtained with the proposed IKGMO is compared with the existing literature methods in Tables 10 and 11 respectively. From these tables, it is identified that, the proposed method yields less cost when compared to existing methods. Further, in this work, the OPF problem is solved using IKGMO algorithm only.

Table 10. Comparison of Literature Methods of Cost Minimization for IEEE-30 Bus System

Table 11. Comparison of Literature Methods of Emission Minimization for IEEE-30 Bus System
After minimizing cost, obtained total power losses are distributed losses to all generators in economic and emission aspects by following the procedure given in section 1. Using this, the obtained results are tabulated in Table 12. From this table, it is observed that, in OPF, due to imposition of inequality constraints on dependent control parameters, the values of the total generation, generation fuel cost, emission and total power losses are increased when compared to NRLF. Because of rescheduling of generations in OPF and distribution of losses, the generation fuel cost is increased by 24.798 $/h when compared to load flow. It is also observed that, in OPF, the generator connected at buses 2 and 8 decreases it's generation drastically when compared to load flow, because of highest fuel cost coefficients.
Similarly, after minimizing emission, the obtained total power losses are distributed losses to all generators and obtained results are tabulated in Table 13. From this table, it is observed that, in OPF, due to imposition of inequality constraints on dependent control parameters, the values of the total generation, generation fuel cost, emission and total power losses are increased when compared to NRLF. Because of rescheduling of generations in OPF and distribution of losses, the emission is increased by 162.1066 ton/h when compared to load flow. It is also observed that, in OPF, the generators connected at buses 5, 11 and 13 have decreased its generation drastically when compared to load flow, because of highest emission coefficients.
In this paper, a new methodology has been presented to remove extra burden on slack bus in both economic and emission aspects. Using this methodology, the effect of nature of power plant (Thermal/Gas) has been analyzed on the system objectives. From the analysis, it has been identified, in economic aspect, the thermal generators have increased its generation whereas Gas generators have decreased and in emission aspect, it is vice-versa. Using slack distribution algorithm, the losses are distributed to generators based on the cost and emission coefficients. And also in this paper, a new algorithm IKGMO has been developed to solve optimization problem with generation fuel cost and emission as objectives. After minimizing, the obtained power losses have been distributed to all generators based on their characteristics using slack distribution algorithm. As this methodology works independent of the size and nature of the system and can be applicable for any type of system. The complete methodology has been tested on IEEE-14 bus and IEEE-30 bus test systems with supporting numerical and graphical results.