(1)
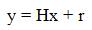
This paper presents a simple algorithm for the Static State Estimation of a Power System. The proposed algorithm makes use of the Weighted Least Square Estimation techniques to estimate the Static State of Power System and hence to analyse the observability of the power system network. Concept of Chi- square test is used to detect the presence of bad measurements in the available data. Developed algorithm is demonstrated for sample 2 bus system.
Selective monitoring of the generation and transmission system has been providing the data needed for economic dispatch and load frequency control. More recently, however, interconnected power networks have become more complex and the task of securely operating the system has become more difficult. To avoid major system failures and regional power blackouts, electric utilities have installed more extensive Supervisory Control and Data Acquisition (SCADA) throughout the network to support computer-based systems at the energy control center. The inputs to the conventional power-flow program are confined to the P, Q injections at load buses and P,|V| values at voltage-controlled buses. If even one of these inputs is unavailable, the conventional power-flow solution cannot be obtained. Moreover, gross errors in one or more of the input quantities can cause the power-flow results to become useless. In practice, other conveniently measured quantities such as P, Q line flows are available, but they cannot be used in conventional power-flow calculations. These limitations can be removed by state estimation.
State estimation plays a very important role in the monitoring and control of modern power systems. The aim of state estimation is to obtain the best possible values of the bus voltage magnitudes and angles by processing the available network data. This paper [1] discusses the state of the art in Electric Power System State Estimation. A real-time model which is a quasi-static mathematical representation of the current conditions in an interconnected power network, is extracted at intervals from snapshots of real-time measurements (both analog and status). This paper [2] describes a generalized, fully developed, estimation approach that fundamentally improves the information extraction process. Its main contribution is the successful inclusion of topology and parameters in the estimation and bad data analysis processes.
There are many techniques to estimate the state of system which are detailed below.
The method of least squares is often used to " best fit" measured data relating two or more quantities. Here the authors apply the method to a simple set of dc measurements which contain errors, and extend the estimation procedures to the ac power system. The best estimates are chosen as those which minimize the weighted sum of the squares of the measurement errors.
The standard technique for solving state estimation problems is to apply the Newton or Gauss- Newton method. While Newton's method has superior convergence properties when the starting point is near the solution, its disadvantage is possible convergence failure on problems that are very nonlinear.
The backtracking idea can be stated as: initially try the Gauss- Newton step; if a step is not acceptable, shorten it as necessary until an acceptable step is found. While sometimes successful, the backtracking strategy has the disadvantage that it makes no further use of the ndimensional quadratic model. Many step-length reductions may be required, entailing unproductive effort.
The roots of the trust region algorithm methods lie in the pioneering work of Levenberg (1944) and Marquardt (1963) for nonlinear least squares problems. They first noticed that when the Hessian is not Symmetric Positive Definite (SPD) in Newton's method, the method may not converge. Adding positive elements (the Levenberg- Marquardt parameter) to the diagonal was suggested.
Various techniques for Dynamic State Estimation[DSE] are also available in the literature. The research [3] presents a bird's eye view on different methodologies and developments in DSE, based on our comprehensive survey of the available literature.
The problem of power system state estimation is a special case of the more general problem of estimation of a random vector x from the numerical values of another related random vector y with relatively little statistical information being available for both x and y. In such cases, the method of least squared error estimation[6] may be utilized with good results and has accordingly been widely employed.
Assume that x is a vector of n random variables X1 ,X2 ……….Xn , y is another vector of 'm' (>n) random variables Y1 ,Y2 ………..Ym and both are related as
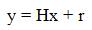
Where 'H' is a known matrix of dimension m X n and r is a zero mean random variable of the same dimension as y. The vector 'x' represents the variable to be estimated, while the vector 'y' represents the variables whose numerical values are available. Equation (1) suggests that the measurement vector 'y' is linearly related to the unknown vector 'x ' and in addition is corrupted by the vector 'r' (error vector).
The problem is basically to obtain the best possible value of the vector 'x' from the given values of the vector 'y'. Since the variable 'r' is assumed to be zero mean, one may take the expectation of equation (1) and get the relation,
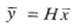
This shows that the load flow methods could be used to estimate the mean values of the bus voltages. However, one would like to estimate the actual values of bus voltages rather than their averages.
One possible way of obtaining of least possible estimate of the vector 'x' from 'y' lies in the use of the method of least square estimation (LSE). To develop this method, assume that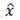 
represents the desired estimate of x so that desired estimate of y is given by the equation.
The error of estimation of y is then given by
The estimate is defined to be the LSE if it is computed by minimizing the estimation index J given by
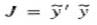
From equation (4) and (5) one gets the following expression for the index:
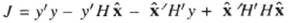
For minimizing J , we must satisfy the following condition
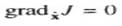
It is easy to check that equation (7) leads to the following result.
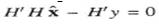
This equation is called the 'normal equation' and may be solved explicitly for the LSE of the vector
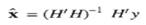
The estimate given in equation (9) is often referred to as the 'ordinary' least squares estimate and is obtained by minimizing the index function that puts equal weightage to the errors of estimation of all components of the vector 'y'. It is often desirable to put different weightages on the different components of 'y' since some of the measurements may be more reliable and accurate than the others and these should be given more importance. To achieve this, we define the estimation index as
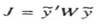
Where W is a real symmetric weightage matrix of dimension mXm. This is often chosen as a diagonal matrix for simplicity.
It is relatively straight forward to extend the method of LSE to the weighted form of J and to derive the following form of the normal equation.
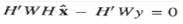
This leads to desired weighted least squares estimate (WLSE):
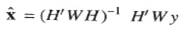
The observability is related to the problem of determining the system state by measuring the output for finite length of time. Hence observability can be defined as,
‘A system is said to be completely observable, if every state X(t0) can be completely identified by measurements of the outputs Y(t) over a finite time interval’. If the system is not completely observable, it means that few of its state variables are not practically measurable and are shielded from the observation. [4] provides a numerical approach to observability analysis. The approach enables observability analysis and restoration (pseudomeasurement selection) in a simple way with iteration, via triangular factorization of the jacobian matrix of the weight least square state estimator.
Consider the static WLSE which serves as the starting point for all the algorithms.
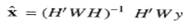
Inverse of information matrix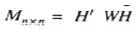 
should exist otherwise there is no state estimate.
This will happen if rank of H equals to n (no. of state variables). Since one can always choose a nonsingular W, if H has a rank n, the power network is said to be observable.
The ability to detect and identify bad measurements is extremely valuable to a load dispatch centre. One or more of the data may be affected by malfunctioning of either the measuring instruments or the data transmission system or both. Transducers may have been wired incorrectly or transducer itself may be malfunctioning so that it simply no longer gives accurate readings.
If such faulty data are included in the estimation algorithm, it will yield unreliable estimates of the state. It is therefore important to develop techniques for detecting the presence of faulty data in the measurement, which are called as bad data detection techniques. In [5], the effect of bad data present in the measurements is studied by using weighted least square estimation.
Let z1, z2 ….. z4 be the measurements of n state variables, and x1, x2…..xn be the estimated values, and if we know the variances of the measurements then the presence of bad data is detected by using the concept of chi-square distribution.
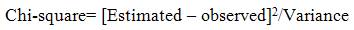
If this value is greater than the standard value of chisquare for given degree of freedom and level of significance, then it indicates that there is presence of bad data.
The main objective of this research is to study the existing methodologies available for estimating the state of the system and to provide an algorithm for estimating the state of system by making use of Least squared estimation technique and weighted least square estimation which is implemented in MATLAB. Observability of the system is also checked by using the same algorithm. The concept of Chi-square test is used to detect the bad data in the measurements.
P1 = -V1 V2 Y(1,2) sin (delta2 );
P2 = V1 V2 Y(1,2) sin (delta2 );
Q1 = Y(1,1) V12 - Y(1,2) V1 V2 cos(delta2 );
Q2 = Y(2,2)V22 - Y(1,2)V1 V2 cos(delta2 );
A simple two bus system is considered with phase angle of bus 1 assumed to be 0° and voltages at the two buses and phase angle at bus 2 are considered as state variables.
System data:
Y=[2 1; 1 2]; delta1=0
Initial Values:
V1 =1; V2=1; delta2 =0;
The MATLAB code is developed for above proposed algorithm and is tested for sample two bus system as shown in Figure 1. The outputs for different cases are listed below.
Output:(LSE Method)Enter number of state variables 3
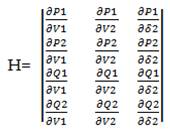
The jacobian matrix is
The coefficient matrix for y is
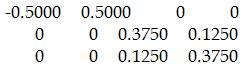
Therefore the estimate for delta and voltages are obtained as
Enter number of state variables 3
The jacobian matrix is
Weighting matrix[1 0 0 0;0 1 0 0;0 0 1 0;0 0 0 1]
The coefficient matrix for Y is
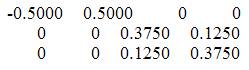
Therefore the estimate for delta and voltages are obtained as
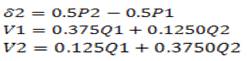
Enter number of state variables 3
Enter the covariance of error[1 0 0 0 0 0;0 1 0 0 0 0;0 0 1 0 0
0;0 0 0 1 0 0;0 0 0 0 1 0;0 0 0 0 0 1]
Enter the measured value of V1 1.2
Enter the measured value of V2 1.1
Enter the measured value of P1 2.3
Enter the measured value of P2 3.5
Enter the measured value of Q1 2.7
Enter the measured value of Q2 4.8
number of iterations 3
The jacobian matrix is
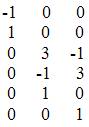
The estimated values of state variables are
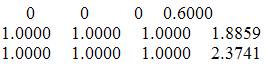
The value of chi square is 2.
The Chi square value is obtained in the above case study. If it is greater than standard value of chi-square for 5% level of significance and degree of freedom=2, it indicates the presence of bad data in the measurements.
Figure 1. Two Bus System
State estimation is an important aspect of secured operation of power system which is very important in today's highly interconnected system. In this paper, an attempt is done to estimate the state of simple system using WLSE technique and hence to check the network observability. The algorithm can be extended for any bus system with initial data available which can be obtained by load flow analysis. Detection of bad measurements is also performed by using chi-square test which is helpful in operating the system securely by removing the bad data detected in the measurements.