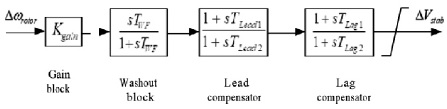
Figure 1. Block Diagram of Classical PSS
A novel Opposition-based Whale Optimization Algorithm (OWOA) is utilized to build a power stabilizer and increase multimachine stability. A Conventional Power System Stabilizer (CPSS) with a lead-lag compensator is employed, and OWOA fine-tunes its settings using an objective function that minimizes the integral absolute error of speed deviations of generator rotors. Various time-domain simulations were performed to validate the superior performance of the proposed Power System Stabilizers (PSS). Furthermore, the performance of the proposed PSS is compared to a Whale Optimization Algorithm (WOA)-based PSS and a conventional PSS. The obtained results demonstrate the effective performance of the proposed OWOA-based PSS for power oscillation damping.
The rise in demand for electricity has resulted in the extension and connectivity of previously established networks. The electricity system is influenced in a variety of ways by these interconnections. The rotor-angle instability is one of the more noticeable phenomena that can occur inside these coupled systems (Padiyar, 2007). Conventional Power System Stabilizers (CPSSs) are employed to mitigate oscillations that can arise between different areas of an interconnected power system. These oscillations are a common occurrence in such systems and can be effectively damped using CPSSs. However, in order to achieve such accurate performance from CPSSs, a CPSS that has been designed correctly is required (Pourbeik & Gibbard, 1998).
There are a number of papers available that point to the use of optimization methods in the design of PSS with reference to power oscillation damping. It is discussed how the robust control theory can be applied to the process of designing a CPSS (Denai & Mohamed, 2005). An enhanced fuzzy logic power stability scheme designed to increase the stability of multimachine power systems is provided in Toliyat et al. (1996). In Hassan et al. (2010), CPSSs are designed in such a way as to suppress electromechanical oscillations.
Jalilzadeh et al. (2011) suggest creating a CPSS and a Static VAR Compensator (SVC) based on Shuffled Frog Leaping (SFL) and Chaos Particle Swarm Optimization (PSO) algorithms to boost the stability of the power system. A coordinated design approach for CPSSs and Automatic Voltage Regulators (AVRs) in an intensely linked system is presented in Dysko et al. (2009).
Ahmadzadeh et al. (2010) proposed a new optimization technique based on the Multi-Objective Genetic Approach (MOGA) with the aim of achieving the best coordinated selection of Power System Stabilizers (PSS) and Flexible AC Transmission Systems (FACTS). The components of FACTS devices include a standard leadlag damping controller built on a Thyristor-based Controlled Phase Shifter (TCPS), Static Variable Compensators (SVC), and a Thyristor-Controlled Series Compensator (TCSC). Bossa et al. (2010) discussed a new field test developed to appropriately assess the PSSs' performance in reducing oscillations in a power station with multiple generators.
Using coordinated gain tuning and coordinated phase and gain tuning as examples, Jabr et al. (2010) demonstrate that conic programming is a highly effective method for resolving issues related to the creation of reliable Power System Stabilizers (PSS). According to Abdel-Magid and Abido (2003), evolutionary algorithms can be utilized to create resilient multimachine power system stabilizers with the best multiobjective design. The power system in France now includes a robust, coordinated Power System Stabilizer+Automatic Voltage Regulator (PSS+AVR) called the "desensitized Four Loop regulator," which was built for the system and is currently being installed (Quinot et al., 1999). In Xin et al. (2008), a multi-objective optimization model is provided for the purpose of determining the feasible stability zone and the highest enduring disturbance rejection for a dynamic model of a smallsignal power system with saturation nonlinearities and disturbance rejection.
In Abido (2002), an innovative method for the optimal design of multimachine CPSSs based on an evolutionary algorithm is presented. Bhattacharya et al. (1997) present an examination of the efficiency of CPSSs considering various system circumstances and operating loads. Abido (1999) proposes a CPSS based on Tabu Search (TS). Sumanbabu et al. (2007) describe a method for simultaneously tuning modern CPSSs in multimachine power systems based on an algorithm called the Bacterial Foraging Algorithm (BFA). Well-known bioinspired algorithms, including the Bacterial Foraging Algorithm (BFA) and Small-Population-based PSO (SPPSO), are used in Das et al. (2008) to construct multiple optimum PSSs in two power systems simultaneously. The proposed approach is based on system identification using a Kalman filter, as presented in Sumina et al. (2011). In Das and Venayagamoorthy (2006), the PSO algorithm has been modified to have a tiny population to create superior CPSSs. Dong-Jie et al. (2002) describe the scheme of an adaptive power system stabilizer using an Artificial Neural Network (ANN). A pole placement method for Power System Stabilizers (PSS) and stabilizers based on Thyristor-Controlled Series Capacitors (TCSC) has also been published in Abido (2000) using the Simulated Annealing (SA) algorithm.
Several studies have proposed various metaheuristic methods for designing Power System Stabilizers (PSSs) in a multimachine setting. Sebaa and Boudour (2009) used a Genetic Algorithm (GA) to determine the optimal locations and designs of PSSs. Ali (2014) proposed the bat search algorithm for the same purpose. Abd-Elazim and Ali (2013) proposed a PSS based on the BFOA algorithm to reduce oscillations in power systems. Abd-Elazim and Ali (2016) presented the Cuckoo Search (CS) algorithm for designing CPSSs in multimachine power systems. Sambariya and Prasad (2015) used the Harmony Search Algorithm (HSA) to create a fuzzy logic power system stabilizer that achieved the best balance between the input and output scaling factors of the fuzzy logic controller (FPSS). Wang et al. (2009) showed that the damping factor and damping ratio are typically used as constraints in the mathematical representation of the fine-tuning process for PSS parameters in multimachine power systems.
The study proposes the creation of a Power System Stabilizer (PSS) for reducing power oscillations in multimachine systems using the Opposition-based Whale Optimization Algorithm (OWOA). The Whale Optimization Algorithm (WOA) is considered a successful optimization algorithm (Mirjalili & Lewis, 2016). The fitness function for setting PSS parameters is based on the minimization of integral time absolute errors of speed deviations of generator rotors. The performance of the system with the proposed PSS is validated by comparing it with systems with WOA-based PSS, CPSS, and without PSSs. The effective performance of the proposed OWOA-based Power System Stabilizers (PSS) is investigated under various operating situations, and it is found to outperform other PSSs.
The conventionally adopted approach for the design of CPSS is the phase compensation approach, which is also used in this work. Figure 1 depicts the transfer function block of CPSS, which includes basic blocks such as the gain block, washout block, lead - lag phase compensation block, and limiter. The rotor speed deviation serves as the input to CPSS, which enters the gain block with gain Kgai.

Figure 1. Block Diagram of Classical PSS
The signal from the gain block enters the washout block with a washout constant of TWF = 10 s. From the washout block, the signal passes through phase compensation blocks with time constants TLead1, TLead2, TLag1, and TLag2.
A stabilizing signal ΔVstab is obtained after phase compensation block. This stabilizing signal is used by exciter of generator to damp out power oscillations. During transient operation, CPSS should stabilize the system.
This work investigates a two-area four-machine testing system that is widely used, as developed and studied by (Kundur et al., 2022). A MATLAB model of the system has been created, as shown in Figure 2, to focus on studying low-frequency fluctuations in interconnected power systems (Kundur et al., 2022; Klein et al., 1992). The testing system comprises two identical areas that are fully symmetrical and connected to each other by two 230 kV lines that are each 220 km long. Each location has two round rotor generators with a rating of 20 kV/900 MVA, and the synchronous machine parameters are identical except for the inertias, which are H = 6.5s in region 1 and H = 6.175s in region 2 (Klein et al., 1992; Kundur et al., 2022). It is assumed that the speed regulators in all thermal plants are identical, and fast static exciters have a gain of 200 (Klein et al., 1992; Kundur et al., 2022). The load is divided among the areas as constant impedances, with area 1 providing 413 MW of power exported to area 2. The differences in generation and transmission losses may vary depending on the level of detail presented in the line and generator representation.

Figure 2. Single Line Diagram of Kundur System
To obtain the optimal parameters of CPSS, the minimization of Integral Time Absolute Error (ITAE) of the speed deviations of generator rotors is considered as the fitness function. The fitness function J is expressed as follows in Equation 1.
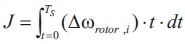
where, ∆ωrotor,i is the speed deflection in ith generator and i= 1,2,3 and 4. Ts is the total simulation time. The fitness function J expressed in Equation 1 is minimized considering the following parameter constraints. The constraints are expressed as in Equations 2 to 6.
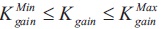
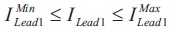
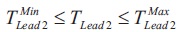
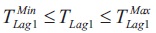
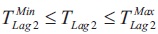
where, Kgain is the gain of PSS and TLead1, TLead2, TLag1, and TLag2 are the coefficients of phase compensation block of PSS. ‘max’ and 'min' superscripts represent maximum and minimum values of the parameters.
As a result, the primary objective in tuning the parameters of PSS is to achieve the lowest possible value of the fitness function J defined in Equation 1, subject to the system constraints expressed in Equations 2 to 6. OWOA is proposed as an answer to the challenges of tuning the parameters of PSS within the scope of this work.
Opposition-based Whale Optimization Algorithm (OWOA) is a type of optimization algorithm used to solve complex optimization problems.
The WOA method is a population-based meta-heuristic optimization technique that was inspired by the bubblenet feeding habit of humpback whales. It is a relatively novel algorithm proposed by Mirjalili and Lewis (2016) and is used to solve a variety of optimization problems (Aljarah et al., 2018; Kaveh & Ghazaan, 2017; Kumar & Rao, 2016; Prakash & Lakshminarayana, 2017; Touma, 2016). This procedure consists of three basic stages such as, encircling the prey, spiral bubble-net feeding behavior, and hunting for prey.
The first stage of the WOA method is called encircling the prey, and it is believed that whales have the ability to locate their prey before encircling it. Whales try to modify their positions in order to approach the prey, which is considered the best candidate solution. Mathematically, this behavior can be described by the Equations 7 and 8.
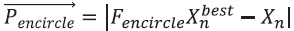
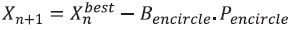
where, Xbest is the best position vector in nth iteration. Bencircle and Fencircle are coefficient vectors. X and Xn+1 are the position vectors in nth and (n + 1)th iterations, respectively. The vectors Bencircle and Fencircle are computed as shown in Equations 9 and 10.
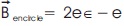
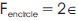
The shrinking encircling mechanism is responsible for achieving the feeding behavior by decreasing the value of e as defined in Equation (9). Since Bencircle depends on e, Bencircle will also decrease as e decreases. Thus, B→ encircle encircle can be regarded as a value randomly chosen from the interval [−e, e]. The position of the new candidate solution can be determined as being somewhere between the position of the current best solution and the position it originally held if the random values for Bencircle are set in the interval [-1,1].
In the spiral updating position phase, the algorithm models the helix-shaped movements made by whales using a mathematical spiral equation, which can be represented as in Equations 11 and 12.
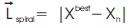
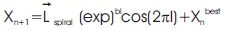
where, Lspiral is the distance between the whale and its prey. A constant called b is used to specify the spiral's shape, and l is any random number in the interval [-1,1].
In addition, during the optimization process, it is assumed that the probability of a spiral updating position phase and a shrinking encircling mechanism is equal. If ρ is a random number between 0 and 1, then the whale's current position vector can be defined in Equation 13.

The solutions that are deemed to be superior will move on to the next phase.
During this phase, whales look for prey in a random manner while taking into account the positions of one another. To carry out this phase of the process, the value of B→encircle is changed so that it is either less than -1 or greater than 1, which compels the agents to advance further inside the search space, allowing for a search on a global scale. The following Equations 14 and 15 illustrates how it is represented.

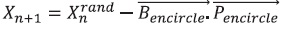
where, Xrandn is a position vector taken at random from the group that is currently being used. The solutions that are judged to be superior are chosen and brought forward to the subsequent iteration. As a result, the procedure in its entirety is carried out again and again until the termination criteria are fulfilled.
Opposition based learning, introduced in Tizhoosh (2005), involves evaluating fitness functions on both randomly generated solutions and their opposite solutions, and selecting the one that produces the minimum value for a minimization problem. This can be represented mathematically as in Equations 16 and 17.
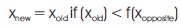
where, xold and xopposite are the old solution and opposite solution.
The opposite number or solution xopposite can be obtained by
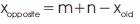
where, xold lies in the range [m,n].
The problem of tuning the parameters of PSSs is addressed by applying OWOA as a solution. The following is an enumeration of the various steps involved in its implementation.
Step 1: Read data from the system and adjust the algorithm control parameters, such as the maximum number of iterations, population size, and boundary conditions.
Step 2: Generate the initial population of solutions by selecting individuals at random from the search space.
Step 3: Generate an opposite number solution from the initially randomly generated solution.
Step 4: Determine the optimal solution by analyzing the objective function.
Step 5: Update the solution according to the updating equation.
Step 6: Choose the more effective solutions to participate in the next iteration.
Step 7: Repeat steps 3 to 6 until one of the criteria for terminating the process has been met.
The simulation results and their discussion are presented in this section, where both the large-signal and small-signal stability test cases are considered for a four-machine system with two areas. The OWOA algorithm is applied to tune the parameters of power system stabilizers. A population size of twenty and a total of one hundred iterations are used for each test case. The system modeling and algorithm implementation are carried out on the MATLAB platform. OWOA has the advantage of requiring fewer algorithm-specific parameters. Table 1 shows the boundary conditions of the PSS parameters.

Table 1. Boundary Conditions of Parameters of PSS
The proposed study considers two test cases for finetuning the parameters of PSSs. The first test case evaluates the robustness of the proposed PSS under small-signal stability, while the second test case evaluates its performance under large-signal stability. Figure 3 shows the simulations in the time domain are presented to demonstrate how the proposed PSSs enhance the overall system functionality.
Figures 4 to 8 show the various parameter for generator, excitation system, steam turbine, transmission line and three-phase fault respectively.
Figure 4. Parameters of Generators

Figure 5. Parameters of Excitation System

Figure 6. Parameters of Steam Turbine

Figure 7. Parameters of Transmission Line
Figure 8. Parameters of Three-Phase Fault
The small-signal stability assessment of the system has been carried out to demonstrate the performance of the proposed PSS. In this scenario, it is assumed that there will be a 10% increase in the voltage reference of generator G1 at 1 s, which will be maintained for 0.2 s. The PSS parameters are fine-tuned using OWOA and WOA, and the results are tabulated in Table 2. The table shows that the minimum value of the objective function J is 0.0015, which is obtained from OWOA. This indicates that the performance of the PSS based on OWOA is superior to that of the PSS based on WOA.

Table 2. Optimal Parameters for Case of Small-Signal Stability
In Figures 9a to 9c, the rotor-angle discrepancies are displayed to demonstrate the performance of the system with the proposed PSS in comparison to the system without PSSs and the system with conventional PSSs. The figure clearly shows that the deviations reach steady-state when the OWOA-based PSS is used in the system. Moreover, the proposed PSS is found to be better than the WOA-based PSS and CPSS. On the other hand, the system without PSS becomes unstable in the event of a small disturbance in the reference voltage at the terminal of generator G1. Figures 10a to 10d illustrate the rotor speed variations after the disturbance, and the same inference can be drawn from the figure's results.
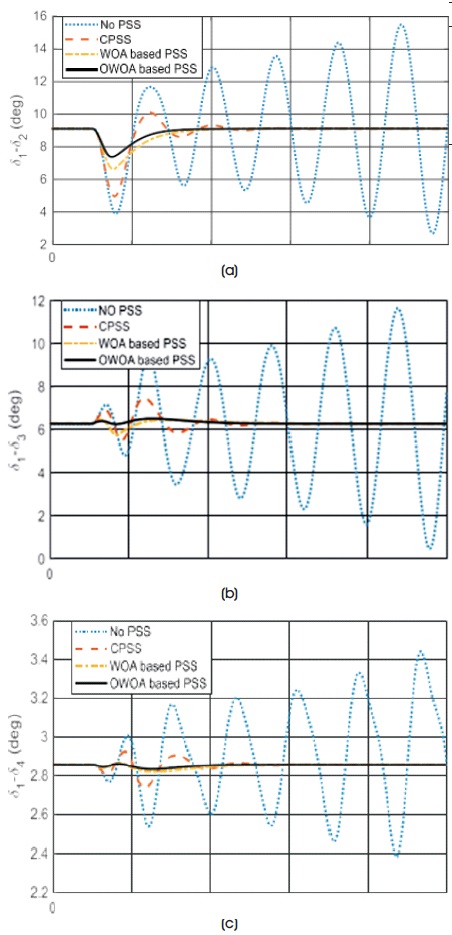
Figure 9. Rotor-Angle Deviations for Case of Small-Signal Stability (a) d1 − d2, (b) d1 − d3, (c) d1 − d4
In this scenario, the performance of the proposed PSS is evaluated to determine if the system can stabilize after significant disturbances. A three-phase fault to the ground is introduced in the middle of the line 7 - 8 at 1 second and is cleared after 0.1 second for the purpose of simulation. In this particular case, the PSS parameters are fine-tuned with the assistance of OWOA and WOA. Table 3 presents the tabulated results of the study. It can be observed from the table that the minimum value of the objective function J is 0.0032, which is obtained from OWOA. Therefore, it can be concluded that the performance of a PSS based on OWOA is better than that of a PSS based on WOA.
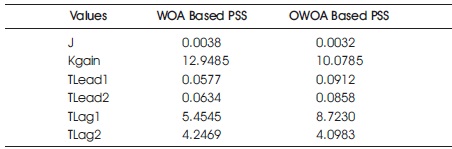
Table 3. Optimal Parameters for Case of Large-Signal Stability
The performance of the system with the proposed PSS is demonstrated through time-domain simulations, in comparison to the performance of the system without PSSs and the system with conventional PSSs. Figures 11a to 11c display rotor-angle discrepancies, and it is evident from the figure that the deviations reach steady-state if the OWOA-based PSS is used in the system. Furthermore, the proposed PSS is found to be better than the WOAbased PSS and the CPSS. The system without PSS becomes unstable in case of a small disturbance in the reference voltage at the terminal of generator G1. Figures 12a to 12d depict the rotor speed variations after the disturbance, and the same aforementioned inference can be derived from the figure results. Therefore, it can be concluded that the OWOA-based PSS performs efficiently than others in the context of power oscillation damping in the case of large signal stability.
In this study, Opposition-based Whale Optimization Algorithm (OWOA) is utilized to fine-tune the parameters of Conventional Power System Stabilizers (CPSS) for power oscillation damping in a widely used two-area four machine test system. The proposed OWOA-based Power System Stabilizers (PSS) aims to minimize the integral errors due to rotor speed variations. Two test cases, namely small-signal and large-signal stability assessments, are conducted to evaluate the proposed PSS's performance, which is compared to that of a Whale Optimization Algorithm (WOA)-based PSS. The findings validate that the proposed PSS exhibits superior performance. Additionally, when compared to the systems utilizing only CPSS and those without PSS, the proposed PSS outperforms both. Future research directions include applying hybrid optimization algorithms, formulating multi-objective optimization problems, designing PSS for renewable integrated energy systems, and testing the proposed PSS's performance on large power systems.