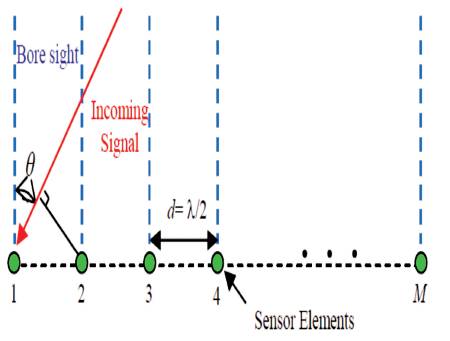
Figure 1. ULA Antenna Configuration [2]
Smart antennas used in new generations of mobile technologies provide a great improvement in detection of the direction of user mobile device. The use of Direction Of Arrival (DOA) algorithms to locate mobile devices is highly applicable due to the improvement of mobile systems to 5G LTE. To select the most appropriate method to work with LTE system, a comparison between the available algorithms in DOA is made. Among the algorithms used were Capon, MUSIC, Root-MUSIC, and ESPRIT. The comparison is made in number of snapshots, SNR, accuracy, and estimation time.
Determining the direction of mobile devices, known as User Equipment (UE) is highly applicable in new technology for many reasons. Services in mobile network depend on the location of UE. Location finding (Direction finding) techniques in a Long Term Evolution (LTE) network has taken advantage due to this [1].
Direction Of Arrival (DOA) estimation with array of antennas signal processing has become very popular in locating mobile devices. As the improvement of mobile communication systems and the increasing number of users, the problem of selecting the appropriate direction finding algorithm becomes even harder. In literature, several studies have been made on algorithms used in direction finding with linear arrays [2].
The purpose of Direction Of Arrival (DOA) algorithms is to use the data received by array of smart antennas on the base station to estimate the angle of arrival of mobile users and the direction of interference signal.
Two important classes of signal processing techniques are the model based approach and the Eigen-analysis method. The model based method assumes that the received data is modeled as the output of a linear shift invariant system. The DOA information can be obtained indirectly from the estimated model parameters such as Capon (Minimum Variance Distortionless Response).
Several Eigen-analysis methods, such as Multiple Signal Classification (MUSIC), root MUSIC, Estimation Signal Parameter via a Rotational Invariant Technique (ESPRIT) have been investigated by many authors [2].
To select of most appropriate method to work with LTE system, a comparison between the available algorithms in DOA is made. Among the algorithms used were Capon, MUSIC, Root-MUSIC, and ESPRIT. The comparison is made with accuracy, and estimation time.
A Uniform Linear Array (ULA) with M elements has been modeled as shown in Figure 1. The elements are separated by d = λ/2, where λ is the incoming signal wavelength.

Figure 1. ULA Antenna Configuration [2]
The signal generated by the source i is the Si(t). If all the signals generated by all the P sources, Si(t), 1 < I < P, then total signal received with added noise by mth array element is [3].
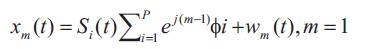
The received signal can also be rewritten in the following form,
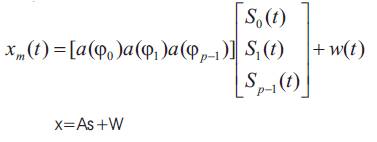
where W represents the noise vector and A represents the steering Matrix,
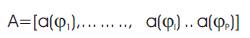
The array steering column vector a(φi ) is defined as,
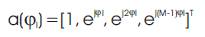
Below is a description of the methods used in this paper [4]:
The Capon's minimum variance method is also known as the Minimum Variance Distortionless Response (MVDR). The goal is to maximize the Signal-to-Interference Ratio (SIR) of received signal. The source correlation matrix Rxx is assumed to be diagonal.
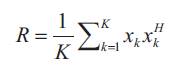
Solving this constraint optimization problem for the weight vector we obtain,

where the received spatial spectrum is an estimated value which represents the direction of incoming signal.
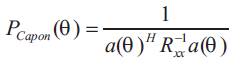
The spatial characteristics of the data for all directions are compactly represented by Rxx , and they are needed to be computed only once [5], [6].
MUSIC stands for MUiltiple SIgnal Classification, one of the high resolution subspace DOA algorithms, which gives the estimation of number of signals arrived, hence their direction of arrival. MUSIC algorithm has been developed to solve the basic problem in the assortment of multiple signals with the terms of Eigenvector, that can distinguish the multiple signals that arrive at the antenna array in the same time. We can consider the direction of the arriving signal, from the maximum point of spatial spectrum of MUSIC method as follows [5].
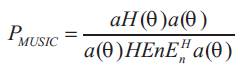
The Root-MUSIC method depends on dividing of the array correlation matrix eigenvectors into two orthogonal subspaces, these are the signal plus noise subspace and the noise only subspace; the steering vectors corresponding to the directional sources are orthogonal to the noise subspace. As the steering vector A is
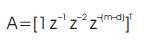
and

Then the roots of Z contain the directional information of the incoming signals. The L closest roots to the unit circle are the roots that correspond to the L incoming signals. These selected roots, by themselves, do not directly represent the incoming angle. For each root, the incoming angle is found by solving,

ESPRIT (Estimation of Signal Parameter via Rotational Invariance Techniques) algorithm is more robust with respect to array imperfections than MUSIC. Computation complexity and storage requirements are lower than MUSIC as it does not involve extensive search throughout all possible steering vectors. The algorithm investigates the division of original array into two sub-arrays [7] .
The steps of ESPRIT are,
1. Calculate the correlation matrix Rxx .
2. Partition the original array into Js1 (matrix of signal eigenvectors), corresponds to the first M largest eigenvalues, and Js2 corresponding to the last M values of the eigenvalues.
3. Using Total Least Squares algorithm to solve,
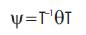
to obtain an estimate of the M ×M matrix.
4. Perform Eigen decomposition of ψ. The diagonal elements are the estimates of Zm that we are looking for.

5. Obtain the DOA using equation.
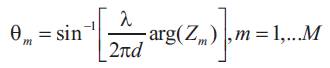
The estimation of different DOA algorithms has been done with MATLAB-2016a. Uniform Linear Array (ULA) with ten antennas has been used to form the antennas in base station. With the spacing between each element is half the wavelength. The simulation has been run for nine signals (representing location of nine users) coming from different angles (-40o , -30o , -25o , -10o , 6o , 10o , 25o , 40o , 45o ). All the sources are considered as of same frequency and uncorrelated. Figure 2 represents the pseudo power spectrum of the all compared algorithms.
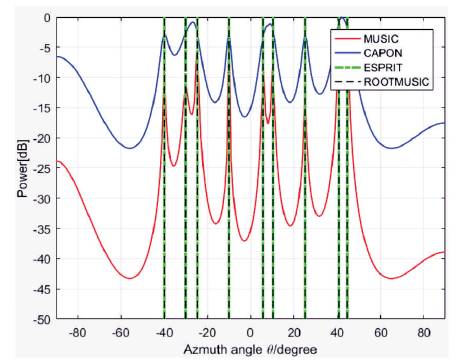
Figure 2. DOA Spatial Spectrum of Capon, MUSIC, Root MUSIC, ESPRIT
Comparison of four algorithms was performed for DOA estimation for varying number of snapshots (N=5, 10, 15, 20, and 50) for nine angles (-40o , -30o , - 25o , -10o , 6o , 10o , 25o , 40o , 45o ) with SNR=-10 dB, array size=10 shown in Tables 1 to 6.
Tables 1 to 4 indicate that for 50 snapshots MUSIC gives an accurate estimation for nine signals. ESPRIT and ROOT MUSIC identifies the nine signals, but the MSE is close, but not exactly zero. For snapshot value less than 50, all methods fail to detect closely spaced signals or replace them with an angle between them, such as replacing 60 and 100 with 80.
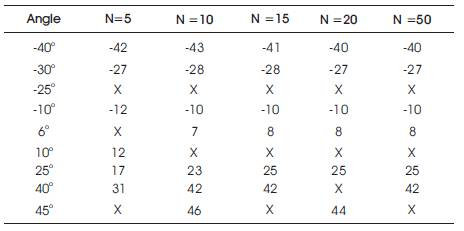
Table 1. DOA Estimation using Capon, SNR=-10 dB, varying No. of Snapshots
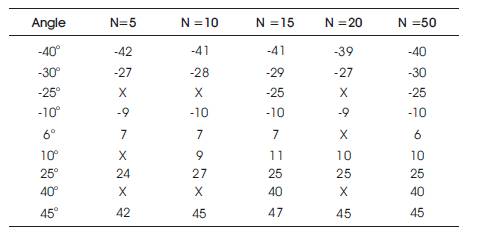
Table 2. DOA Estimation using MUSIC, SNR=-10 dB, varying No. of Snapshots
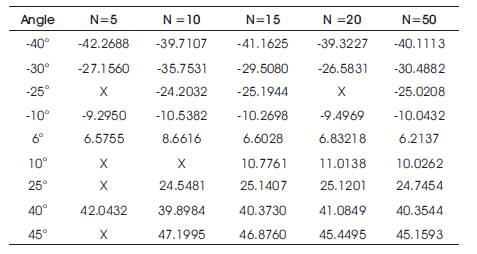
Table 3. DOA Estimation using Root MUSIC,SNR=-10 dB, varying No. of Snapshots
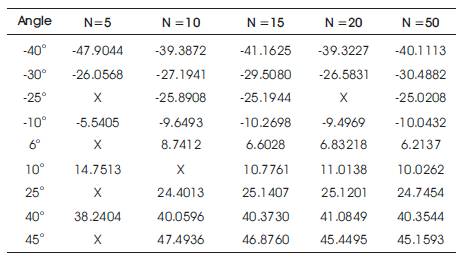
Table 4. DOA Estimation using ESPRIT, SNR=-10dB, varying No. of snapshots
As the number of snapshots increases to 100, peaks in the spectrum become sharper and deeper, and thus means improvement of the resolution capability of MUSIC as shown in Figure 3. The same improvement is shown when increasing the SNR as in Figure 4.
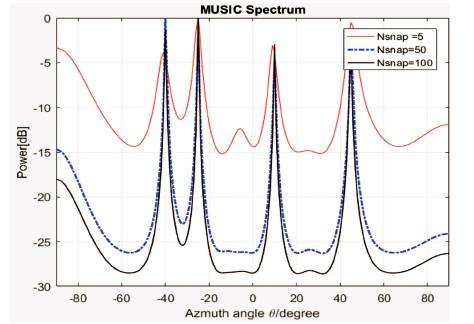
Figure 3. Pseudo spectra of MUSIC with varying number of Snapshots
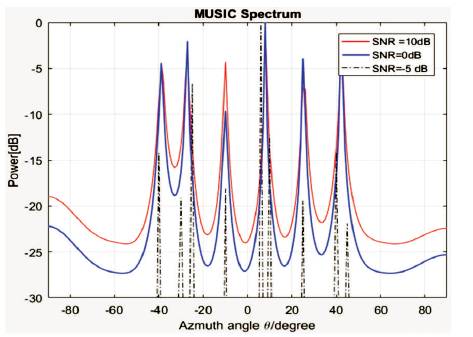
Figure 4. Pseudo spectra of MUSIC with varying SNR
Furthermore, study of DOA estimation has been performed for various SNR values with 50 snapshots, and DOA=-400 (Table 5). Results indicate that as SNR decreases, the both: ESPRIT and ROOT MUSIC are unable to detect the angle correctly as compared to MUSIC.
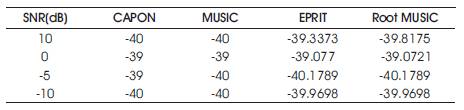
Table 5. DOA Estimation in CAPON, MUSIC, ESPRIT, ROOT_MUSIC, No. Snapshots =50
Last compression between DOA methods was in estimation time with varying number of snapshots (5, 10, 15, 20, and 50). The results show that ESPRIT produces the best results in computing the direction of targets in less time (Table 6).
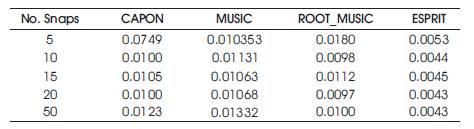
Table 6. DOA Estimation Time (in seconds) for CAPON, MUSIC, Root MUSIC, ESPRIT
This paper shows that, the direction of arrival algorithms that are based of Eigen decomposition performed better than conventional algorithms. It also shows the precedence of MUSIC algorithm to other Eigen-analysis algorithms (ESPRIT, Root-MUSIC).
MUSIC algorithm has shown better results when varying the number of snapshots taken from arrived signal. Even with targets that are close to each other by less than 50 MUSIC, ESPRIT and Root-MUSIC still can identify them correctly.
Different values of SNR,results in giving the highest rank to MUSIC algorithm as the most accurate algorithm, which provides high resolution even with low SNR values.
As the DOA estimation time plays a great factor in the new mobile technology, the algorithm that provides the least estimation time represents the most desired algorithm. ESPRIT produced the least amount of time in estimating the direction of multi-users. That's why it represents an appropriate candidate for 5G technologies.