
Figure 1. A Unit Cell Structure View of C10H13NO3S
2,2-Dimenthyl-N-(phenylsulfonyl)acetamide, C10H13NO3S is one of the derivative of sulfonamide drugs, which uses to treat tuberculosis, urinary tract infection and act as anti-microbial agent. In this study, we focus on the computational and theoretical study of C10H13NO3S by using a Density Functional Theory (DFT) method as our main quantum mechanics computational technique to investigate and analyze the geometry and electronic structures of C10H13NO3S. All DFT simulations were carried out using Quantum Espresso and Gaussian 09 program packages. From the computed results, the lattice parameters (a, b, c, and β), geometrical parameters (bond distances, bond angles, and dihedral angles), electronic structures (total energies, dipole moments, HOMO-LUMO energy gaps, and others ) of C10H13NO3S molecular system also included and discussed in this study.
2,2-Dimenthyl-N-(phenylsulfonyl)acetamide, C10H13NO3S is one of the derivatives of sulfonamide drugs (Gowda et al., 2009; Tačić et al., 2017 and Sulfa drug, n.d). Sulfonamide drugs are the first successfully synthesized drugs discovered by a German bacteriologist in the year 1932 that are used in anti-microbial activities (Sulfa drug, n.d). Sulfonamide has the ability to interfere in the PABA (p-aminobenzoic acid) (Tačić et al., 2017). So, it can prevent the growth and multiplication of bacteria and micro-organisms by inhibiting the synthesis of folic acid in the human body. The sulfonamide drugs can be used to fight over the Gram-positive bacteria and Gram-negative bacteria, i.e. Klebsiella, Salmonella, and Escherichia coli (Tačić et al., 2017). In addition, the sulfonamide drugs may also be effective in the treatment of urinary tract infection, tuberculosis, and some forms of malaria (Demircioğlu et al., 2018). In recent years, it may also act as an anti-infection agent of burn. With the good performance as bacteria and micro-organism inhibitor, sulfonamide drugs still maintain its popularity and position as one of the good choices of anti-microbial agent in the medical industry although it is already being explored about more than 70 years (Tačić et al., 2017). Nowadays, more and more attentions are given in the computational and experimental studies on the derivative of sulfonamide drugs, i.e. its geometry and electronic structures (Demircioğlu et al., 2018). For example, Zeynep Demircioglu and his friends investigated the geometry and electronic structure of (Z)-N-(2-((3-nitrobenzylidene) amino)phenyl) benzenesulfonamide, and (Z)-N-(2-((4- nitrobenzylidene) amino)phenyl) benzene sulfonamide in 2018 (Demircioğlu et al., 2018). They studied that compounds were not only measured using Fourier Transform Infrared Spectroscopy (FTIR), Nuclear Magnetic Resonance (NMR) and X-ray Diffraction techniques, it may also be conducted using Density Functional Theory (DFT) method by employing B3LYP/6-311++G**. However, there are no any computational and theoretical studies on C10H13NO3S molecular system. In this study, only a Crystallographic Information Framework (CIF) file is obtained from Cambridge Crystallographic Data Centre (CCDC) as input data for these calculations (Gowda et al., 2009). So that, the main aim of this study is to carry out the computational and theoretical investigations on C10H13NO3S molecular system. To achieve this purpose, one of the quantum mechanical computational methods, which is known as DFT was used to study the geometry and electronic properties of C10H13NO3S. In this computational study, the geometry structures, such as lattice parameters, bond lengths, bond angles, and dihedral angles were calculated. Besides, the electronic properties, i.e. total energy, Highest Occupied Molecular Orbitals (HOMO), Lowest Unoccupied Molecular Orbitals (LUMO), and band gap energy were also included in this study.
All the DFT calculations were performed on personal computer using Quantum Espresso and Gaussian 09 program packages (Giannozzi et al., 2009; Frisch et al., 2009). A CIF file was obtained from CCDC (Gowda et al., 2009) as the input source for computatonal calculations. The full geometry optimization calculation was performed using a unit cell of C10H13NO3S with DFT method together with PBE and BLYP functionals through Quantum Espresso program package. The optimized lattice parameters, i.e. a, b, c, and β were determined in this work. Figure 1 shows the unit cell structure view of C10H13NO3S. Moreover, a single molecule of C10H13NO3S was used as the host enviroment for geometry optimization calculations in Gaussian 09 software to find the equilibirum structure and lattice parameters using Becke's Three Lee-Yang-Parr (B3LYP) functional with four difference basis sets, which includes 6- 31G, 6-31G**, 6-31++G, and 6-31++G**. Figure 2 shows a single molecule of C10H13NO3S molecule structure view. The optimized single molecular structure obtained was used to calculate the total energy, Highest Occupied Molecular Orbitals (HOMO), and Lowest Unoccupied Molecular Orbitals (LUMO). Besides, the HOMO, LUMO surface plots and the Molecular Electrostatic Potential (MEP) mapped plots were also illustrated using GaussView 5.0 software package (Frisch et al., 2009).

Figure 1. A Unit Cell Structure View of C10H13NO3S
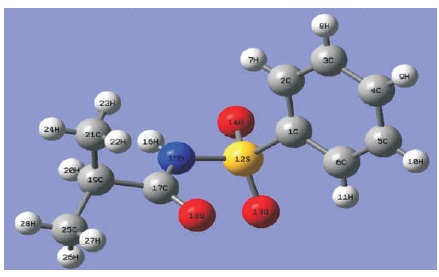
Figure 2. A Single Molecule Structure View of C10H13NO3S
Table 1 shows the optimized lattice parameters (a, b, c, and β) of C10H13NO3S using PBE and BLYP functionals in Quantum Espresso software package. All optimized lattice parameters are compared with the experimental results (Gowda et al., 2009). Both of the computational results show good agreement with the measurement data. In Table 1, it is observed that both of the optimized lattice parameters obtained from PBE and BLYP functionals are slightly smaller than the experimental values. These mean that the optimization process is shrinking the total size of unit cell with the PBE and BLYP functionals as compared with experimental results. In Table 1, the computed data noted that the computational lattices a, b, and c obtained from PBE functional are 3.60%, 3.47%, and 3.51% smaller than the experimental results, while the percentage differences between the experimental data and BLYP functional obtained are 3.15%, 3.21%, and 2.99%. PBE functional has decreased the lattices a, b, and c by 0.213 Å, 0.744 Å, and 0.3022 Å. In the case of BLYP functional, the lattices a, b, and c, are 0.187 Å, 0.69 Å, and 0.2592 Å, shorter than the experimental results. From the comparison data in Table 1, it is concluded that the size of unit cell in BLYP functional is slightly larger than that of PBE functional. Besides, the computed data clearly noticed that the lattice β obatined from PBE functional is 106.282o, and it has a difference of 0.58% as compared to experimental value. In BLYP functional, the computed angle of β is 106.199o, which is of 0.66% difference with that of experimental result. Table 2 summarizes the computed geometry parameter results of PBE and BLYP functionals using Quantum Espresso software package. As can be seen in Table 2, the findings noticed that the bond distances obtained from PBE and BLYP fucntionals are slightly longer than experimental values. The percentage differences for PBE functional fall in the range of 0.12%-4.21% as compared with those of experimental results, while for BLYP functional, the percentage differences fall in the range of 0.99%-4.93%. In C10H13NO3S, both PBE and BLYP calculations undergo least percentage difference at the bond distance of N15 -C17 , and undergo greatest percentage difference at C19 -C21 bond distance.The bond distance differences between PBE functional and experimental results are only 0.00167 Å for bond length of N15 -C17, and 0.06447 Å for the bond length of C19 -C21. For BLYP functional, the bond distances of N15 -C17 and C19 -C21 are about 0.01381 Å and 0.07615 Å, respectively, which are slightly longer than the experimental results. The bond angles and dihedral angles obtained from PBE and BLYP functionals are also included in Table 2. The dihedral angle of C6 -C1 -S12 -N15 obtained from both PBE and BLYP functionals are 118.92o and 118.80o, which possess 1.04% and 1.13% difference with the experimental results. Table 3 summarizes all the optimized geometrical parameters (i.e. bond distances, bond angles, and dihedral angles) for a single molcule of C10H13NO3S using B3LYP functional and difference basis sets used with employing Gaussian 09 software package. In Table 3, it can be noticed that the computational results obtained from B3LYP/6-31G** and B3LYP/6-31++G** methods are more in good agreement with the experimental results. For B3LYP/6-31G** and B3LYP/6-31++G** levels of calculations, the largest bond distance percentage difference are contributed by the bond distance of C19 -C21 with the amount of 4.73% and 4.84%. The bond distances of C19 -C21 are increased by 0.07289 Å and 0.07454 Å. The smallest bond distance percentage difference falls on the C17 -O8 bond distance, with the corresponding percentage of 1.05% and 1.20% for B3LYP/6-31G** and B3LYP/6-31++G** methods if compared with the measurement data. For B3LYP/6-31G and B3LYP/6-31++G, the largest bond distance percentage difference is S12 -O13 bond length, with the percentage of 12.63% and 12.62% larger than the experimental value, while the bond of N15 -C17 is the smallest bond distance percentage difference, with the percentage of 0.58% and 0.53% as compared with experimental data. For the bond and dihedral angles, again it is clearly observed that B3LYP/6-31G** and B3LYP/6-31++G** methods are more close to experimental results if compared with B3LYP/6-31G and B3LYP/6-31++G levels of calculations. In Table 3, it is also noticed that the highest bond angle percentage difference obtained from B3LYP/6-31G** and B3LYP/6- 31++G** fall in the angle of C1 -C2 -C3 in the molecular system. The corresponding bond angle percentage difference are 1.39% and 1.34% as compared with the experimentally observed data. Both of 6-31G** (B3LYP/6- 31G** method) and 6-31++G** (B3LYP/6-31++G** method) have the same dihedral angle (C6 -C1 -S12 -N15), which is 120.13o in this study. For basis set 6-31G and 6- 31++G, both of them also obtained the same dihedral o angle in C6 -C1 -S12 -N15 with the value of 120.07. In Table 3, it is concluded that the methods of B3LYP/6-31G** and B3LYP/6-31++G** are selected to determine the optimized geometry structures of C10H13NO3S in this study since the percentage difference in bond distances and bond angles do not exceed 5%. Although the percentage differences in computed bond angles for B3LYP/6-31G and B3LYP/6-31++G levels of calculations also not exceed 3%, both B3LYP/6-31G and B3LYP/6-31++G methods are not recommended to use in C10H13NO3S molecular system. The difference between experimental and computational values are obtained in this study due to the fact that computational calculations are performed in gaseous phase system, while bulk system is used in the experiment (Ramya et al., 2013; Novena et al., 2017).
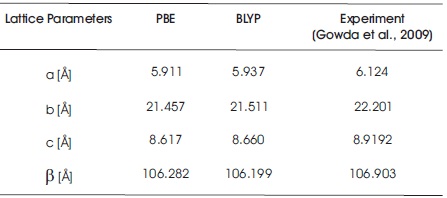
Table 1. Lattice Parameters obtained from PBE and BLYP Functionals
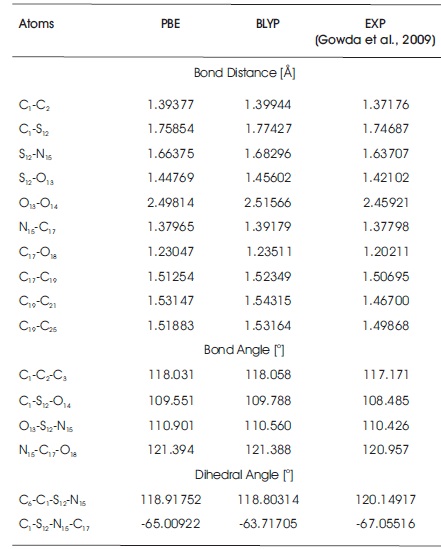
Table 2. Optimized Geometry Structures of C10H13NO3S using Quantum Espresso Package
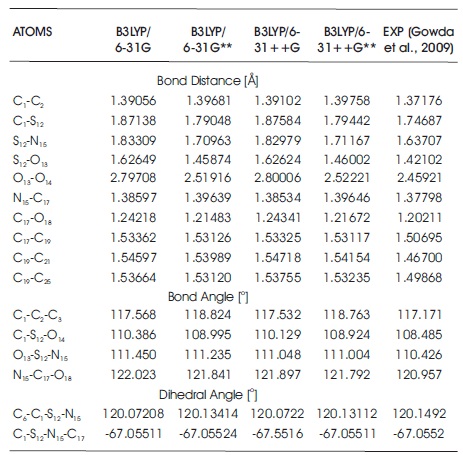
Table 3. Optimized Geometry Structures of C10H13NO3S using Gaussian 09 Program
Table 4 summarizes all electronic structures, such as total energies, HOMO, LUMO, HOMO-LUMO energy gaps, ionization potentials, electron affinitys, and dipole moments of C10H13NO3S. In Table 4, it is noted that the total energies obtained from B3LYP/6-31G, B3LYP/6-31G**, B3LYP/6-31++G, and B3LYP/6-31++G** methods are - 29037.48 eV, -29047.3828 eV, -29038.39 eV, and - 29048.13 eV, respectively. The total energies obtained from B3LYP/6-31G and B3LYP/6-31++G levels of calculations are more close to each other, whereas B3LYP/6-31G** and B3LYP/6-31++G** methods have the similar total energies. The calculated dipole moment for B3LYP functional with employing 6-31G, 6-31G**, 6-31++G, and 6-31++G** basis sets are 6.38 debye, 5.08 debye, 6.49 debye, and 5.23 debye. To predict the chemical reactivity, strength, and stability of C10H13NO3S molecule, Frontier Molecular Orbital (FMO) energies are also presented in Table 4. In this work, the energy of HOMO uses to determine the ability of donating the electrons in C10H13NO3S molecular system, whereas LUMO energy predicts the ability of accepting the electrons (Bouchoucha et al. 2018). In DFT calculations, higher the energy value of HOMO/LUMO, better the ability to donate/accept the electrons. The computed HOMO energy for B3LYP functional with employing 6-31G, 6- 31G**, 6-31++G, and 6-31++G** basis sets are -7.8913 eV, -8.3593 eV, -8.2519 eV, and -8.7169 eV, while the computed LUMO energy are -1.7845 eV, -1.1529 eV, -2.1707 eV, and -1.5644 eV. As can be found from the table, the HOMO-LUMO energy gap for B3LYP/6-31G** and B3LYP/6- 31++G** methods are 7.2064 eV and 7.1525 eV, respectively, which are slightly larger than those of B3LYP/6- 31G and B3LYP/6-31++G. The HOMO-LUMO energy gap obatined from B3LYP/6-31G level of theory is 6.1068 eV, while for B3LYP/6-31++G method, the computed energy gap is 6.0812 eV. These calculated HOMO-LUMO energies obtained are slightly higher with those of sulfonamide derivatives (Al-Sehemi 2011; Mahmood et al., 2016; Dhas & Daniel, 2017). These energy gaps are not only used to study reactivity and stability of C10H13NO3S, it can also be employed in calculating the conductivity of title compound. In this study, the results of ionization potentials and electron affinities of C10H13NO3S molecule are determined since the negative signs of both HOMO and LUMO energies are obtained from the DFT calculations (Ramya et al., 2013). With these computed HOMO-LUMO energies of title molecular system, the chemical reactivity, such as electrophilicity index, hardness, chemical potential, and softness of C10H13NO3S molecule can be studied. The HOMO and LUMO mapped plots for B3LYP functional with employing 6-31G, 6-31G**, 6-31++G, and 6-31++G** basis sets are presented in Figures 3 and 4, respectively. As can be seen from the diagrams, the electron density distributions of HOMO and LUMO show reasonable agreement in this study. These are the nature of charge transfers within the molecular system. The electron density distributions of HOMO are localized on whole C10H13NO3S molecule, while for LUMO, the electron density distribution is strongly focused on the region near phenyl ring and sulfonamide group. The findings obtained are close to several substituted sulfonamides, which are studied by Al-Sehemi (2011), Mahmood et al. (2016), and Dhas & Daniel (2017). To understand how molecular interactions are within C10H13NO3S molecule, Molecular Electrostatic Potential (MEP) mapped plots of title molecular system are illustrated in Figure 5. This MEP mapped plot is very useful in indicating and differentiating the net electrostatic effect of C10H13NO3S molecular system according to its total charge distribution of the title molecule, which is correlated with the electronegativity and dipole moment (Bendjeddou et al., 2016). MEP visualised the polarity of C10H13NO3S molecule according to the colour appeared around the molecules. Red region presents the most negative electrostatic potential, while blue colour shows the least negative or in order words most positive electrostatic potential (Demircioğlu et al., 2018). Four MEP mapped plots obtained from B3LYP/6-31G, B3LYP/6-31G**, B3LYP/6-31++G, and B3LYP/6-31++G** methods provide the similar results. For example, the regions around three oxygen atoms (i.e. O13 , O14 , and O18 ) present the red colour MEP mapped plots, while the region around the hydrogen atom (i.e. H16) shows the deep blue colour MEP mapped plot. The rest of atoms appear in white or light blue colour region in MEP mapped plot. The computed results obtained concluded that the regions around three oxygen atoms (i.e.O13, O14, and O18) will undergo the electrophilic reactivity, which can accept the electrons, whereas the region around the hydrogen atom (i.e. H16) will undergo the nucleophilic reactivity, which can donate electron (Demircioğlu et al., 2018).
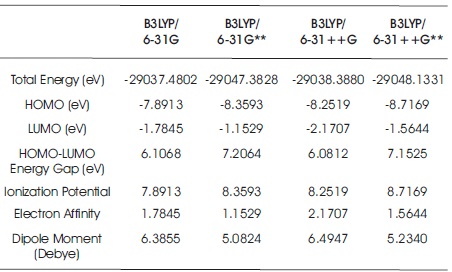
Table 4. Electron Affinity, Ionization Potential, Dipole Moment, Total Energy, and FMOs of C10H13NO3S Molecule
Figure 3. Calculated HOMO Mapped Plots using DFT/B3LYP Method with Employing (a) 6-31G, (b) 6-31G**, (c) 6-31++G, (d) 6-31++G** Basis Sets
Figure 4. Results of LUMO Mapped Plots using DFT/B3LYP method with Employing (a) 6-31G, (b) 6-31G**, (c) 6-31++G, (d) 6-31++G** Basis Sets
Figure 5. MEP Mapped Plots obtained from DFT/B3LYP Method with Employing (a) 6-31G, (b) 6-31G**, (c) 6-31++G, (d) 6-31++G** Basis Sets (Note: R - Red, B - Blue)
In this presented work, DFT quantum mechanical computational method has been used to investigate the geometry and electronic properties of C10H13NO3S molecular system. For a single C10H13NO3S, the geometrical parameters obtained from B3LYP/6-31G** and B3LYP/6- 31++G** levels of calculation show a good agreement with the experimental results. All the calculation results including geometry parameters (bond distance, bond, and dihedral angles), total energies, dipole moments, and FMO energies are quite similar using B3LYP/6-31G** and B3LYP/6-31++G** methods. The HOMO-LUMO energy gap among the B3LYP/6-31G, B3LYP/6-31G**, B3LYP/6-31++G, and B3LYP/6-31++G** levels of calculations fall in the range of 0.224 eV - 0.265 eV, while the dipole moments obtained are between 5.08 debye and 6.39 debye. From the MEP surface plot, all the four basis sets show that the most negative electrostatic potential were localized on the region around O , O , and O atoms, while the less 13 14 18 negative electrostatic potential region was focused on H 16 atom. Besides, the optimized geometry parameters results (bond angles, bond, and dihedral angles) obtained from both Quantum Espresso and Gaussian 09 program packages were compared and found to be in good agreement.