A quantum wave packet can be defined as a superposition of a set of energy levels. The energy levels for this can be , electronic states in atoms , vibrational and rotational states in molecules and phonon-number states in quantum optics. When the dynamics of this wave packet is observed, it is initially well localized in space and remains in this form till few classical time periods of its motion. Afterwards the distortion creeps in due to the underlying quantum phenomenon of dephasing of constituent subsidiary waves. In simple one dimensional harmonic oscillator quantum well, a localized wave packet will show the motion of classical particle and is never distorted due to equidistant energy levels of its energy spectra. But in other quantum systems where the separation of the energy levels increases as a function of the principal quantum number 'n', the wave packet spreads after few classical time periods, collapses after few more classical time periods and revives later on. The wave packet revivals occur periodically after a time known as the revival time. In between two revival times, initially localized wave packet spreads significantly and enters so called collapsed phase. This behavior demonstrates, quantum behavior of wave packets.

The phenomenon of collapses and revivals of the wave packets was first discussed in [1]. After that, many authors had discussed this phenomenon focusing on the infinite square well potential [2-4], harmonic oscillator potential [5- -6] and the Rydberg Atoms[7—8]. Certain variants of the infinite square well have also been discussed as the infinte square well with δ potential at the centre [1], asymmetric infinite square well [9] and the finite square well [10]. The united approach of all these authors relevant to the demonstration of the phenomenon of the collapses and revivals of the wave packets is to localize the initial Gaussian wave packet inside the well and then visualize the dynamics of the wave packet with the passage of time. The autocorrelation function has also been plotted by some authors to give the evidence of the collapses and revivals of the wave packet [11]. The effects of collapse and revival of wave packets in monolayer and bilayer graphene in the presence of an external perpendicular magnetic field are investigated in [12]. A complementary approach to existing theoretical models and experimental systems has been presented in [13]. It relies on laser-cooled neutral atoms which orbit around an optical nanofiber in an optical potential produced by a red-detuned guided light field.

This paper deals with the construction of a quantum wave packet by superimposing the vibrational states of CO molecule and its time evolution. Vibrational motion of molecules can be treated using Morse potential model. The properties of these vibrations are critical in interpreting infrared and raman spectra , for the understanding of chemical dynamics and understanding of chemical dynamics ,for the understanding of heat capacities of gas phase and liquid phase systems. The paper is organized as sections describing the purpose, the proposed system including quantum mechanical model taken for the diatomic vibrations and review of the time evolution of the quantum wave packets, the mathematical tool for observing the revivals and collapses of wave packets, the probability density function and the autocorrelation function.

The molecular vibrations give rise to vibrational energy levels which are designated by the vibrational quantum number n. The purpose of this paper is to superimpose some specific energy levels to construct a wave packet and study its time evolution, and to obtain a wave packet having a Gaussian distribution of probability density which is centered about a specific vibrational quantum number v=15, for which the weighted summation of wave functions from v=1 to v=25 is to be carried out. The weighted summation implies that the wave functions are multiplied with weight factors having a Gaussian distribution i.e. the contribution of the wave functions of the levels lying close to mean vibrational quantum number is maximum and decreases with increase in the difference lv-15l. After the construction of wave packet, its time evolution is studied. Since the vibrational motion is simple to and fro motion, the time evolution of Gaussian wave packet should follow the same pattern. The time period of one complete to and fro motion is termed as classical time period. After each classical time period, the wave packet shows spreading. The amount of spreading is indicated by the auto correlation function. The spreading of wave packet is substantial after many classical time periods. At a time scale called as revival time, the wave packet regains its original shape. The time evolution is to be studied up to few revival time periods.

The theoretical model chosen to describe the vibrational motion of non-rigid molecule is elaborated in the following sections.

2.1 A Model for Molecular Vibrations

Molecular spectra is primarily divided into three categories; electronic spectra, rotational spectra and vibrational spectra. This paper presents time evolution of GWP (Global Warming Potential) constructed from vibrational levels of a CO molecule.

Vibrational motion of molecules can be treated using the harmonic oscillator model. The harmonic oscillator model is the simplest approximate model for the vibrational motion of the diatomic molecule. For the harmonic oscillator, potential curve is parabolic. Since a diatomic molecule is an example of two particles linked by a central force, this two body problem can be reduced to a single body problem using the concept of reduced mass, which is represented by µ and is given as,

(1)

 

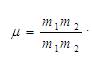
The Schrödinger equation for harmonic oscillator is [15]

(2)

 

Here, ψ represent the wave function , E is the energy of the system ,h is the Plank's constant and k is the force constant.

It is convenient to simplify Eq. (2) by introducing the dimensionless quantities. Let us introduce a dimensionless variable:

(3)

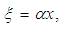
where α is constant having dimensions of inverse of length. Thus Eq.(2), takes the form,

(4)

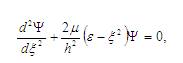
Where,

Here 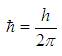is the reduced Plank's constant and ω₀ is the frequency of the harmonic oscillator which is determined by the force constant and is given by,

(5)

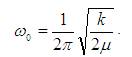
The energy Eigen values (symbolized by ) 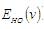and the normalized wave function (symbolized by ) for the harmonic oscillator are given as,

(6)

(7)

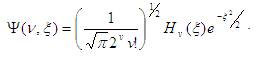
Where 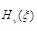are Hermite polynomials of order v, and v represents the vibrational quantum number.

The harmonic oscillator model for the vibrational motion shows discrepancies for the real diatomic molecules because the real potential of diatomic molecule deviate more and more from the parabolic potential with the larger deviation of intermolecular distance 'r', from equilibrium intermolecular distance 'r_e'. So a more e practical model for vibrating molecule is Morse potential. The Morse potential is defined below

(8)

Where E_D is dissociation energy of the rigid molecule and β is the Morse parameter controlling the width of the potential well.

The energy levels in this case (symbolized by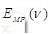 are given by,

(9)

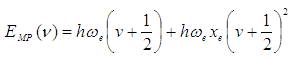
With : c=2.99792458X108

h=6.6260755X10-34

Here,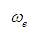 is the harmonic wave number of vibration and 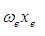is the anharmonic constant. These can be determined from the observation of two or more vibrational energy transitions.

(10)

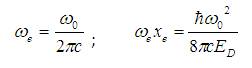
The wave functions in this case (symbolized by ψ(v,x) are given by,

(11)

Where

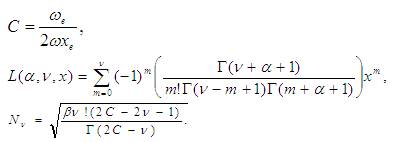
Here

C is a constant

L(α,ʋ,x) are the associated Laguerre polynomials and N_U is a vector of normalization constants.

The eigen functions of the Morse potential are given in terms of the variable 'x' defined below

(12)

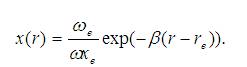
2.2 Time Evolution of the Quantum Wave Packet

The time-dependent wave function for the quantum wave packet formed as a superposition of vibrational states is given as [1],

(13)

 

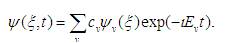
Here the coefficients 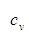are the weighting factors in the superposition, which are given in terms of the initial wave function as

(14)

 

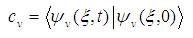
The weighting probabilities are modeled as a Gaussian distribution,

(15)

 

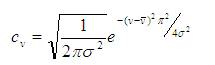
This model is preferred as it provides a symmetrical distribution in v with mean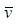

With the assumption that the weighting probabilities are peaked around a mean value, it is reasonable to suppose that the states with energy near the mean value, contribute for the formation of wave packet. This allows expanding the energy in a Taylor series in v around the central value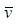

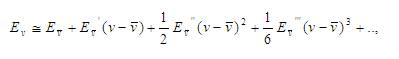
(16)

 

where each prime denotes a derivative.

The derivative terms in Eq.(16), define the time scales as given below [5]:

(17)

 

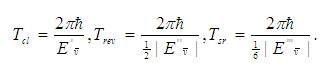
The first time scale is the classical time period for the shortest closed orbit. It controls the initial behavior of the wave packet. The second time scale is called the revival time. It governs the appearance of the fractional revivals and the full revivals. The third time scale is the super revival time. It is a larger time scale as compared to classical and revival time. In terms of these time scales, the Eq. (16) can be expressed as,

(18)

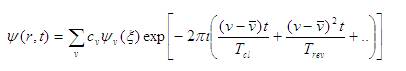
The expansion (18) shows that the time evolution of wave function is governed by these three time scales, which in turn are controlled by quantum number v. For small values of t, the first term in Eq. (19) dominates. Thus during this interval motion of wave packet is approximately periodic in time with period . As t increases, the second term in phase modulates this behavior, causing the wave packet to spread and collapse. However, at time equal to revival time ,the second term in phase equals 2πi and once again the motion is governed by the first term. As a result, the wave packet regains its initial shape. This is called a full revival. Similarly at the super revival time, again the contribution of the third term is 2πi , the wave form reforms into a single wave packet that resembles the initial one better than the full revival at revival time. This new structure is called a super revival.

3. The Probability Density Function and the Autocorrelation Function

The probability density function is used to plot the shapes of the wave packet at various times. This function is defined as follows

(19)

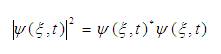
Similarly, the absolute square of autocorrelation function is defined as [11],

(20)

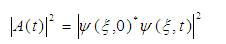
It gives a measure of the overlap between the wave packet at time t=0 and at later time t.

Substituting equation (13) in equation (20) ,|A(t)|2 yields,

(21)

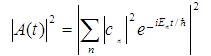
Using equation (15) for C_n coefficients, plots of |A(t)|2 are  obtained to observe the revivals and collapses of GWP constructed from the vibrational energy levels of CO.

4. Results and Discussions

A weighting factor with central value of 15 and CO as an example of diatomic molecule has been taken. Now for the molecule CO, the vibrational constants, the classical time period and the revival time period are,

 

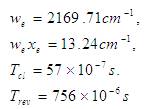
The figures 1 through 4 are the plots of the probability density function at various instants of time. Figure 1 is the plot of the probability density function at time t=0. The wave packet is at the r.h.s. of the equilibrium inter-atomic distance 'r_e'. Figure 2 is the plot of the probability density function at time 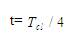. Clearly the wave packet is moving towards the l.h.s. of the potential. Figure 3 is the plot of the probability density function at time 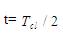. Here the oscillatory behavior of the wave packet is seen. This is due to momentum gain by the wave packet as a consequence of contact with high potential wall at the left most end of the Morse potential. Figure 4 is the plot of the probability density function at time,

(22)

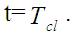
Figure (5) shows the plot of absolute square of the autocorrelation function versus reduced classical time (the ratio of the classical time period and the classical time for the primitive path). It is clear that the wave packet spreads more and more after every classical time period as the peaks of autocorrelation functions are decreasing. Ultimately the wave packet will collapse. But at the revival time period, the wave packet revives to its original state. This fact is made lucid from the plot of absolute square of the autocorrelation function versus reduced revival time (the ratio of the revival time period and the revival time for the primitive path), Figure (6). It is seen that full revivals occur at times t=k*T_rev /2, when all vibrational Eigen States have accumulated a phase of 2*π*k with k = 1, 2, 3,. This result is supported by the findings of [14]. The smaller peaks show the existence of fractional revivals.

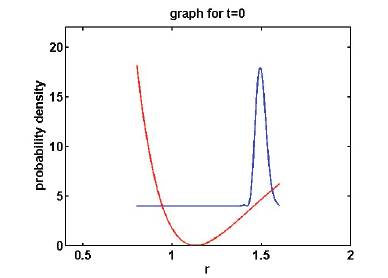
Figure 1. Probability Density plot at time t=0

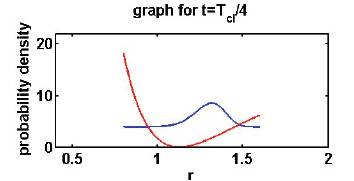
Figure 2. Probability Density plot at time t= T_cl/ 4

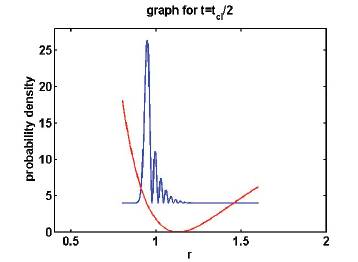
Figure 3. Probability Density plot at time t= T_cl/ 2

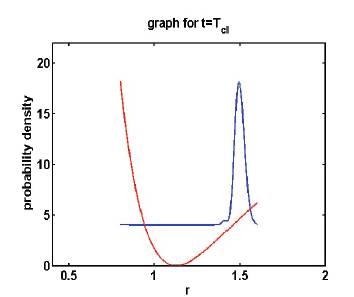
Figure 4. Probability Density plot at time t= T_cl

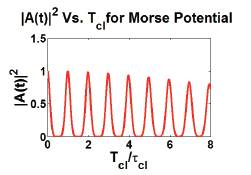
Figure 5. Autocorrelation function vs. reduced classical time

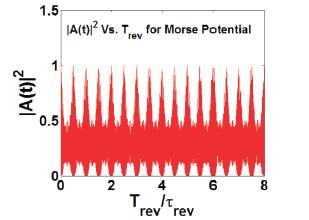
Figure 6. Autocorrelation function vs. reduced revival time

Conclusion

The revival structure of quantum wave packet constructed by superimposing the vibrational states of the CO molecule has been analyzed. From the energy spectrum, it is possible to predict the motion and type of revivals that the wave packet undergoes. It is shown that motion is simple to and fro motion and the quantum wave packet constructed by superimposing the vibrational states of the CO molecule shows the exact revival pattern along with the fractional revivals.

Acknowledgement

The work is accomplished with the help of resources of department of Physics, DAV college, Amristar.

References

[1]. C. U. Segre, and J. D. Sullivan, (1976). “Bound-state wave packets, '' Am. J. Phys, Vol. 44, pp.729-732.

[2]. D. L. Aronstein, and C. R. Stroud, (1997). 'Fractional wave-function revivals in the infinite square well, '' Phys. Rev. A, Vol. 55, pp. 4526—4537.

[3]. R. W. Robinett, (2000). “Visualizing the collapse and revival of wave packets in the infnite square well using expectation values, '' Am. J. Phys, Vol. 68, pp.410-420.

[4]. D. F. Styer, (2001). “Quantum revivals verses classical periodicity in the infinite square well, ” Am, J. Phy., Vol. 69, pp. 56-62.

[5]. R. W. Robinett, (2004). “Quantum wave packet revivals,” Physics Reports, Vol. 392, pp.1-119.

[6]. Robert Bluhm, V. Alan Kostelecky, and James A. Porter, (1996). “The evolution and revival structure of localized quantum wave packet, ” Am. J. Phys, Vol. 64, pp.944-953.

[7]. L. S. Brown, (1973). “Classical limit of hydrogen atom, '' Am. J. Phy. Vol. 41, pp. 525-530.

[8]. Z. D. Gaeta, and C. R. Stroud, (1990). “Classical and quantum mechanical dynamics of a quasiclassical state of the hydrogen atom,' 'Physical review A, Vol. 42, pp. 6308 - 6313,

[9]. Todd K. Timberlake, and Seth Camp, (2011). “ Decay of wave packet revivals in the asymmetric infinite square well,” Am. J. Phys, Vol. 79, pp.607-614.

[10]. Anu Venugopalan, and G. S. Agarwal, (1999). “Superrevivals in the Quantum dynamics of a particle trapped in a finite square well potential,'' Phys. Rev. A Vol. 59 (2),, pp.1413 - 1422.

[11]. Michael Nauenberg, (1990). “Autocorrelation function and quantum recurrence of wave packets,'' Journal of Physics B, Vol. 23, pp. L385-L390.

[12]. Demikhovskii, V. Ya.; Telezhnikov, A. V.; Frolova, E. V.; Kravets, N. A., (2013). “Mesoscopic states in graphene in a magnetic field: Collapse and revival of wave packets”, Low Temperature Physics, Vol 39, Issue 1, pp. 18-25.

[13]. Fam Le Kien, K. Hakuta, D. Reitz, P. Schneeweiss, and A. Rauschenbeutel, (2013). “Quantum dynamics of an atom orbiting around an optical nanofiber”, Phys. Rev. A 87, 063607.

[14]. B. Gruner, M. Schlesinger et al, (2011). “Vibrational relaxation and dephasing of Rb2 attached to helium nanodroplets,” Phys. Chem. Chem. Phys., Vol 13, pp. 6816–6826.

[15]. Popat S. Tambade, (2011). “Harmonic oscillator wave function and probability density plots using spreadsheets,” Lat. Am. J. Phy. Educ. Vol. 5, pp. 43 - 48.