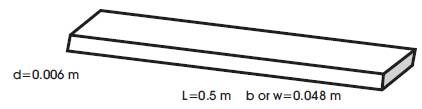
Figure 1. Rectangular Cross Section of the Beam Indicating the Dimensions not to Scale
This paper deals with evaluation of the natural frequencies of a cantilever beam with fixed dimensions and material. The necessary boundary conditions are applied and the natural frequencies are evaluated by 3 methods viz a) analytically, by using relevant formulae, b) by using the concepts of FEM and MATLAB software, and c) by experimental analysis.
There will be a discrepancy in the above values of the natural frequencies. The experimental value is taken as a benchmark and the deviation of the value by analytical and FEM methods are minimized or the dynamic characteristics of the beam structure are improved by employing the principles of Structural Dynamic Modification (SDM). Model updating is one of the techniques of SDM used to converge the values of the natural frequencies closer to the experimental value.
SDM can be defined as a method by which the dynamic behavior of a structure is improved by predicting the modified behavior brought about by adding modifications like masses, links, dampers, flats, etc., or by variations in the configuration parameters of the structure itself [1]. Analytical and experimental analysis techniques have been extensively used for the dynamic analysis of the mechanical structures [1]. The required data for the structural modification is got either from analytical model or from the experimental model. On the other hand, to establish a predetermined dynamic behavior of structure is not an easy task, even after the modal parameters or FRFs are known. Extra efforts are needed for the measurements of FRFs to construct the full FRF matrix of the structure [3]. The dynamic characteristics for any system can be improved based on the results of SDM methods. This avoids the repetition of analytical solution or experimental time consumption [4]. Thus the computational effort is reduced and also the expenditure involved in a structure operating at resonance can be avoided. Because at the resonance, i.e. when the operating frequency matches the natural frequency, maximum disturbance and distraction occurs to the system or structure.
FEM tools Model Updating includes utilities and methods to update finite element models to better match the reference targets like test data. Model updating works by modifying the mass, stiffness, and damping parameters of the FE model until an improved agreement between FEA data and test data is achieved.
The process begins with the formulation of an initial FE model using initial values for the update parameters. The FEA results that will be used to check correlation with the test are computed using the FE model with the current update parameter values. The model updating method uses the discrepancy between FEA results and test, and sensitivities to determine a change in the update parameters that will reduce the discrepancy. The FE model is then reformed using the new values of the update parameters, and the process repeats until some convergence criteria, analyzed by means of correlation functions, is met.
A beam specimen is taken for analysis and comparison. The dimensions of the beam are length=0.5m, width=0.048 m and depth= 0.006 m. The material of the beam is Mild Steel with Young's Modulas of Elasticity, E= 2.1x1011 N/m2 and Material density =7850 kg/m3 . The cross section of the beam is rectangular, so Moment of Inertia, I= bd3 /12. Figure 1 represents the beam specimen.

Figure 1. Rectangular Cross Section of the Beam Indicating the Dimensions not to Scale
As already discussed, natural frequency is a criterion for all the structural elements and it is necessary to calculate it. The basic characteristic equation according to FEM to calculate the natural frequency is |K-λM|=0, where K is the stiffness matrix, which is symmetric matrix reflecting the property of the material, λ is the Eigen value=ω2 and ω = 2πf and M is the mass matrix [5].
The steps involved in SDM are as follows:
i) Calculate the eigen values of the beam by the above formulae.
ii) For confirmation, the eigen values are calculated analytically also.
iii) Compare these values with that of the experimental values .
iv) Parameters for modification to be selected.
As defined earlier, model updating is a process of correcting the numerical values of individual parameters in an analytical FE model using data obtained from an associated experimental model such that, the updated model correctly describes the dynamic properties of the specimen. In the present work, single parameter optimization is chosen and this is achieved by two methods.
Central difference formula for first order differentiation is given by:

In this method, the individual components of the matrix are differentiated as shown below:
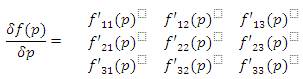
Where f' (p) are the first order derivatives of each element of f(p) with respect to design parameter p.
The primary objective of this work is to compare the natural frequencies of the specimen, with respect to experimental results, analytical methods and Finite Element Methods. There will definitely be a discrepancy in these results which is termed as the deviation [6].
The secondary aim of this work deals with the concept of Model Updating. Owing to the fact that, experimental results are always accurate; an attempt is made to get the FEM results closer to the experimental value of the natural frequency [7]. The goal of Model updating is to reduce the deviations due to inaccuracies in the finite element model and in predicting results from the inaccurate model. Model testing or experimental model analysis is the process of determining the modal parameters (frequencies, damping factors, modal sealing) of a linear, time invariant system by way of an experimental approach. The nodal parameters may be determined by finite element analysis or by formulas and one of the common reasons for the experimental modal analysis is the verification correction of the results obtained by FEM.
In practice, natural frequencies and mode shapes (i.e., Eigen values and Eigen vectors) of an analytical model do not match very well with experimental measured frequencies [6]. Thus updating the existing dynamic model on the basis of modal test data is very important for predicting actual behavior of the structure. The use of Model Updating procedures allows the designers to tune the analytical model so as to get minimum deviation between the experimental value and analytical characteristics. This helps to gain more confidence in the further use of predicted model [8].
l=0.5 m, b or w=0.048 m, d=0.006 m, Material=Mild Steel, E=2.1x1011 N/m2 , ρ=7850 kg/m3 .
The first natural fundamental [9] is given by,
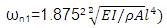
where, I=bd3 /12
A=bxd
Substituting all the above in equation (3),
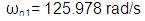
where, ω=2πf
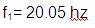
Similarly the second natural frequency [9],
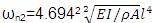
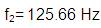
A program is designed to calculate the natural frequencies of the cantilever beam in MATLAB and the results are obtained as follows:
f1 = 20.131 hz and f2 = 198.593 hz
The test specimen is taken for vibration analysis and fixing one end rigidly, the test piece acts a Cantilever beam. Test sensors are fixed and the frequency is directly read on the analyzer. The experimental setup is shown in Figure 2 and Figure 3. The values of f1 and f2 by experimental analysis are 18.50Hz and 116.50 Hz respectively. This is read from the graph which is shown in Figure 4 [14].
The values of the first and second natural frequencies obtained by the three methods are tabulated in Table 1. The first natural frequency also called as the fundamental frequency is of primary importance.

Figure 2. Clamping of the Test Specimen as Cantilever Beam

Figure 3. Specimen Fixed with Sensors

Figure 4. The Natural Frequencies of the Cantilever Specimen obtained experimentally
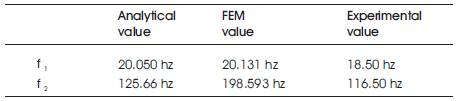
Table 1. Comparison of the First and Second Natural Frequencies using 3 Methods
It is seen that, the values obtained by analytical and FEM calculations are comparatively higher than the experimental values. This is due to the under estimation of the global mass matrix and over estimation of the global stiffness matrix as substantiated in reference [8] .
Now to get the FEM value nearer to the experimental value, Model Updating is to be done, wherein the dimensions of the specimen will be changed so as to get the FEM value closer to the experimental value. This is achieved by using Taylors series given by,
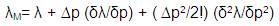
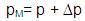
where, λM = Modified natural frequency,
pM = Modified design parameter.
The first order Eigen value derivative (δλ/δp) and the second order derivative (δ2λ/δp2 ) are obtained by |K-λM|Φ1 =0.
In the present paper, only the first order derivative is considered, which is given by,

The derivatives of the element stiffness (δK/δp) and element mass (δM/δp) matrices are calculated using two methods as explained before:
a) Central Difference Method,
b) Direct Differentiation Method.
Considering the first natural frequency, an effort is done to get the FEM value closer to the experimental value by updating the dimensions of the specimen or model [5] .
The geometric parameters and the material properties of the structures have a significant effect on Dynamic characteristics like Eigen values, Eigen vectors, etc., [10]. The procedure of Model Updating includes the change of the geometrical parameters of the structure so as to get the dynamic characteristics closer to the experimental results. Model Updating is done for the 3 parameters viz, length, width and depth, keeping 2 of the parameters as constants and varying the other.
Figures 5(a), (b) and (c) show the graph drawn by considering the dimensions of the cantilever beam just to ascertain the effect on the natural frequency when two parameters are kept constant and one of them is varied [14].
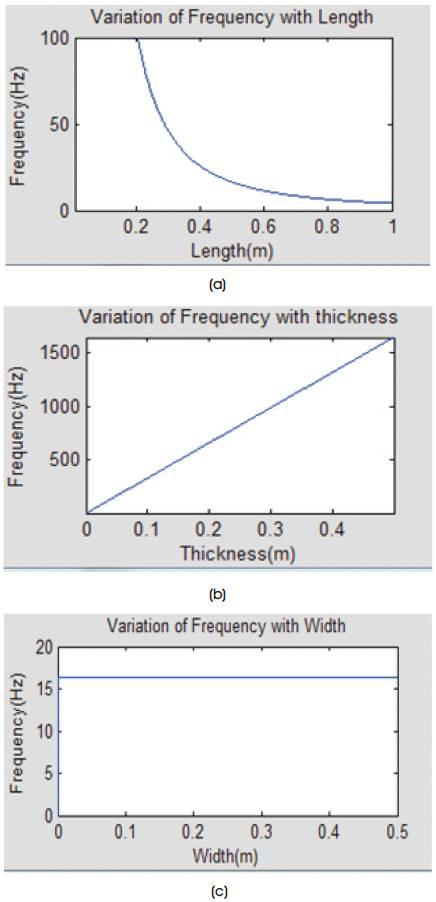
Figure 5. Variation of Natural Frequency with (a) Length, (b) Thickness/Depth and (c) Width
The graphs indicate that the thickness or depth and the length of the specimen are the affecting parameters for the natural frequencies. Hence criteria to decide the parameters depend on the analytical results. So length and depth of the specimen are to be varied as they affect the natural frequency to a greater extent. On the contrary, the variation in the width of the beam will negligibly affect the natural frequency as seen from the graph (Figure 5(c)) and so is not considered for variation.
The impact load is the criterion which primarily depends on the depth than on the length of the beam.
Hence length is kept as a constant in the present problem and depth is considered for model updating.
The value of the depth by both the above methods is 0.00552 m to get the natural frequency f1 =18.5604 Hz, which is very close to the experimental value of 18.5 Hz.
There is an error in the natural frequency of the cantilever beam calculated analytically, by FEM method and by experimental methods. This difference of values is minimized by the concept of Model Updating.
The thickness or depth parameter is considered for model updating, as any variation in this, change the natural frequency to a considerable extent. The model updating is done by two methods viz, DDM and CDM.
The length of the beam is kept as a constant parameter due to the reason that almost in all the practical applications, length is not varied.
It is found that, there is a negligible effect on the natural frequency by varying the width to a greater extent.
Thus, the concept of Model Updating has its feature to avoid the manufacturing cost and the computing time that may have incurred due to faulty dimensions or due to the usage of conventional manufacturing procedures.
The concept of SDM and model updating is widely used in various mechanical components such as design of drilling machines, slotting machines, cutting machines, etc, [11]. As a case study, design of tennis racket is based on this study by S. Lammens et al., [8]. Predominantly these principles are used for the analysis of beam structures. Many researchers have investigated the analysis for various boundary conditions, cross sections and different material compositions also. The same is quoted in references [12], [13].
It is highly recommended, as the techniques that followed in this paper are very much useful for the optimum design of any mechanical or civil structural components. With the help of these techniques, ie, CDM and DDM, an accurate design is possible without the danger of resonance effect.
SDM - Structural Dynamic Modification
FEM - Finite Element Method
FRF - Frequency Response Function
DDM - Direct Differentiation Method
CDM - Central Difference Method