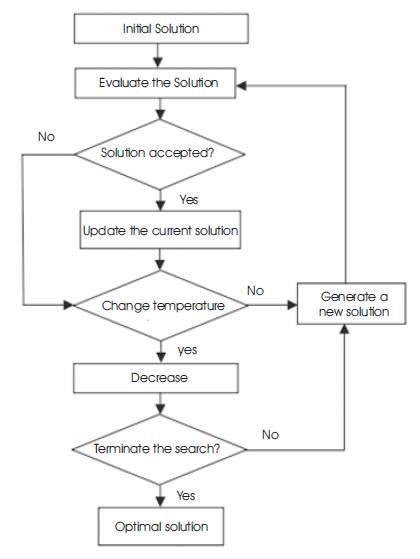
Figure 1. The Structure of the Simulated Annealing Algorithm
Titanium and its alloys are classified into difficult to cut materials. To machine such materials economically, the optimized process parameters play significant role. Therefore the experiments have been planned and conducted using Design of Experiments. The experiments are conducted under different machining environments such as dry, flooded and Minimum Quantity Lubrication (MQL) machining with different tool materials such as uncoated, Chemical Vapour Deposition (CVD) and Physical Vapour Deposition (PVD) coated tools. In this study, Taguchi's L orthogonal array is 27 used to perform the experiments. The results obtained from these experiments are used to develop multiple regression model in terms of input process parameter. The same model is used as a fitness function for Simulated Annealing (SA) to optimize the process parameters for minimum surface roughness. The optimum results from SA is compared with Taguchi methodology and validated with Regression Analysis. The optimum parameters obtained both in Taguchi's methodology and Simulated Annealing are flooded machining, high cutting speed, low feed rate, low depth of cut and CVD coated tool.
The Ti-6Al-4V is an Alpha-Beta grade - 5 Titanium Alloy. Titanium alloys are classified as difficult to machine material due to their mechanical properties especially the hardness, tensile stress at high temperatures, differences of structure with a variable quantity of the alpha phase, morphology of the transformed beta phase, low thermal conductivity, low modulus of elasticity and high chemical reactivity. Ti-6Al-4V is most widely used in variety of weight reduction applications such as aerospace and jet engine components; automotive; medical applications such as implants, bone joint replacements, and surgical instruments; marine applications; chemical industry; turbine blades, etc [1, 14]. The advantages of Ti-6Al-4V alloys are relatively less in weight, high strength to weight ratio, bio-compatibility, low thermal and electrical conductivity, corrosion resistance, ability to maintain high strength at high temperatures, etc.
Cutting fluids are commonly applied in the machining zone to improve the tribological characteristics of machining processes to dissipate the heat, improve the tool life, reduce work piece thermal deformation, improve the surface roughness and flush away the chips from the cutting zone. The advantages of flooded/conventional use of the cutting fluids are questioned lately due to their negative effects such as deteriorated employee health, environmental pollution and cost. In recent years, lot of research has been carried out to avoid the use of cutting fluids in machining. Because of them, some alternatives have been sought, one of the alternatives is Minimum Quantity Lubrication (MQL) machining in place of Flooded machining. E.O. Ezugwu et al. [1] have reviewed the main problems associated with the machining of titanium alloys, tool wear, and the mechanisms responsible for tool failure. It was found that the straight tungsten carbide (WC/Co) cutting tools continue to maintain their superiority in machining titanium alloys. This paper also reviewed special machining methods, such as rotary cutting, the use of ledge tools, Minimum Quantity Lubrication (MQL), etc.
Azlan et al. [2] applied Genetic Algorithm (GA) to optimize cutting conditions for minimizing surface roughness in end milling machining process. In their study, experiments are conducted using Design of Experiments (DOE), these results are used to optimize the process parameter for minimizing surface roughness using regression model and GA. These results indicated that, the GA approach successfully applied to minimize the surface roughness. The effects of process parameters on tool wear and optimal parameters have been found using Taguchi's design approach. The results indicate that the selected process parameters affect significantly on the TiC coated carbide tool [3]. M. Venkata Ramana et al. [4] have worked on performance evaluation and optimization of process parameter in turning of Ti-6Al-4V alloy with different coolant conditions on surface roughness using uncoated carbide tool. From the experimental investigations, the cutting performance on Ti-6Al-4V alloy with synthetic oil is found to be better as compared to dry and soluble servo cut in reduction of surface roughness. The results from ANOVA indicated that, the synthetic oil is more effective under high cutting speed, high depth of cut and low feed rate as compared to dry and soluble servo cut oil.
Shiba Narayan Sahu et al. [5] optimized process parameters for Electro Chemical Machining to get better result of Material Removal Rate (MRR), and Surface Roughness (SR) for hard materials. In this paper, MRR and SR values are optimized by Simulated Annealing (SA) and the effect of input parameters are determined by Taguchi Design while machining EN-19 tool steel. SA was successfully integrated with regression model equation for two contradicting objectives of ECM process. Farhad Kolahan et al. [6] used Multi Objective Optimization for machining processes to achieve simultaneously several objectives such as increased product quality, reduced production time and improved production efficiency. In this, an approach that combines grey relational analysis, and regression modelling to transfer the values of multi responses obtained from Taguchi method design of experiments into a multi objective model has been used. This approach is implemented on turning process of St 50.2 Steel. After model development, Analysis of Variance (ANOVA) is carried out to determine the adequacy of the proposed model. Turning process modelling based on grey relational analysis, and multiple regression models is successfully implemented and developed models is optimized with simulated annealing algorithm. Material Removal Rate and Surface Roughness are combined in a regression model using grey relational grades.
Azlan et al. [7], proposed two integrated Simulated Annealing and Genetic Algorithm (SA – GA – type 1 and SA – GA – type 2) soft computing techniques to find out optimum process parameters to minimize the surface roughness. Results of these two methods arrived at optimum process parameters leading to minimum surface roughness as compared to experimental data. Hsien Ching Chen et al. [8] analyzed the variation of cutting velocity and work piece surface finish on Wire Electrical Discharge Machining (WEDM) process parameters during manufacture of tungsten profiles. A method of integrating Back Propagation Neural Network (BPNN) and Simulated Annealing Algorithm (SAA) was used to determine an optimum parameter for WEDM process to minimize the surface roughness. The results among Taguchi's method, BPNN and SAA were compared and validated with confirmation experiments. Seung et al. [9] proposed an optimization methodology for the arrival of optimum parameters in Electro Discharge Machining (EDM) in die sinking applications. In this, Counter Propagation Neural Network is used to create model for simultaneously maximizing the material removal rate and minimize the surface roughness. These models are validated with Simulated Annealing Approach and confirmation tests.
The demands of modern engineering products require more precise details and the control of surface roughness has become more important. It has been investigated that surface roughness greatly influences the functioning of the parts. Manufacturing involves various processes to turn raw materials to finished products to be used for a variety of purposes. Whatever may be the manufacturing process used, it is not possible to produce perfectly smooth surface. Among all the manufacturing processes, machining is most widely used to obtain best dimensional accuracy and surface finish. Hence, the improved qualities of product and the economics of the manufacturing operation are very important considerations to produce product having functional and visual appeal.
In real world machining applications, it is required to maximize the production with minimum cost and high quality. The quality refers to the surface roughness of the machined component. The conventional optimization methods such as Taguchi's Robust Design Methodology, Factorial Technique, and Response Surface Methodology (RSM) technique are used to optimize the process parameters. Now a day's soft computing techniques also called as non conventional techniques are mostly used to optimize the process parameters. These methods are more precise, with less time and cost. The recognized soft computing techniques to optimize the process parameters are Neural Networks (NN), Genetic Algorithm (GA), Fuzzy Logics (FL), Simulated Annealing (SA), Tabu Search (TS), Ant Colony Optimization (ACO), Particle Swarm Optimization (PSO), etc. The SA is mostly used for solving complex problems to obtain optimal parameters.
Dr. Taguchi build on the work of Plackett and Burman by combining statistics and engineering to achieve rapid improvements in product designs and manufacturing processes. His efforts led to a subset of selecting experiments commonly referred to the Taguchi Method. Major Premises of Taguchi Techniques are focused on the robustness of the product; make the product correctly in spite of variation in materials and processes. The Quality Loss Function (L(y)), provides both a conceptual and a quantifiable means to demonstrate the impact of deviation from target [10].
Taguchi calls common cause variation the “noise”. Taguchi's approach is not to eliminate or ignore the noise factors; Taguchi techniques aim to reduce the effect of the noise on the product quality. The Loss Function can help put the cost of deviation from target into perspective. The signal-to-noise ratio provides a measure of the impact of noise factors on performance. The larger the S/N, the more robust the product is against noise. Calculation of the S/N ratio depends on the experimental objective: Bigger-the- Better, Smaller-the- Bigger, Nominal-the-Better.
Taguchi designs have been developed to study factors at two-levels, three-levels, four-levels and even with mixed levels. Types of Taguchi Designs include two-level designs the L4, L8, and L16 matrices. Taguchi screening designs for three levels exist. The L9 looks at 4 factors at 3 levels. An L27 can be used to study up to 13 factors at 3 levels, and an L81 can evaluate up to 40 factors at 3 levels. The linear graph is a graphical tool that facilitates the assignment of factors, and their interactions to the experimental matrix. Some experimenters find the interaction tables developed from the linear graphs to be easier to use.
The regression analysis is used for modeling and analyzing several variables, when the focus is on the relationship between a dependent variable and one or more independent variables. More specifically, regression analysis helps to understand how the typical value of the dependent variable changes when any one of the independent variables is varied, while the other independent variables are held fixed. Regression analysis is widely used for prediction process performance characteristics. The regression analysis is of two types. These are simple linear regression analysis, multiple regression analysis [11]. In this work, a prediction model is developed for surface roughness using multiple regression analysis from experimental results.
Once the regression model is ready, the optimum process parameters can be determined using non-conventional optimization methods. Unlike other non-conventional optimization methods, simulated annealing process uses single point search method. Simulated annealing method looks like the process of molten metal through annealing. At high temperatures, the atoms in the molten metal can move freely with respect to each other, but as the temperature is reduced, the movement of the atoms gets limited. The atoms start to obtain order, and finally form crystals having the minimum possible energy. However the formation of the crystal mostly depends on the cooling rate. If the temperature is reduced at a very fast rate, the crystalline state may not be achieved; instead the system may end up in a polycrystalline state, which may have a higher energy state than the crystalline state. Therefore, in order to achieve the absolute minimum energy state, the temperature is to be reduced at a slow rate. The process of slow cooling is known as annealing in metallurgical practice. The simulated annealing procedure simulates this process of slow cooling of molten metal to achieve the minimum function value in minimization problem. The cooling phenomenon is simulated by controlling a temperature-like parameter using the concept of the Boltzmann probability distribution [12].
Simulated annealing algorithm begins with an initial point and a high temperature (T). A second point is created at random in the vicinity of the initial point and the difference in the function values ΔE at these two points is calculated. If the second point has a smaller function value, the point is accepted; otherwise the point is accepted with a probability exp(-ΔE/T). This completes one cycle of the simulated annealing procedure. In the next cycle, again another point is created at random in the neighbourhood of the updated current point and the Metropolis algorithm is used to accept or reject the point. In order to simulate the thermal equilibrium at every temperature, a number of points (n) are usually tested at a particular temperature, before reducing the temperature. The algorithm is terminated when a sufficiently small temperature is obtained. The initial temperature T and number of iterations N performed at every temperature are two important parameters, which govern the successful working of the simulated annealing procedure [9]. The structure of the simulated annealing algorithm is shown in Figure 1.
In this work Taguchi's methodology, Regression analysis and Simulated Annealing (SA) are used for the optimization of process parameters and prediction of output performance characteristic.

Figure 1. The Structure of the Simulated Annealing Algorithm
To obtain the optimum conditions for minimum surface roughness in turning of Ti-6Al-4V alloy under different machining conditions, the Taguchi's methodology is used. Statistical software Minitab is used to perform Analysis of Mean (AOM) and Analysis of Variance (ANOVA) [13]. The different cutting conditions used in this work are given in Table 1. The surface roughness (Ra) is measured using a Mahr marsurf GD 25 PC based surface roughness tester. It is equipped with a diamond stylus having a tip radius of 2 μm.
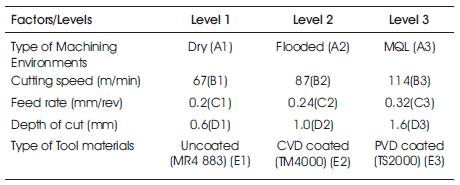
Table 1. Experimental conditions
The experiments are conducted under different machining environments such as Dry, Flooded and MQL on HMT NH 22 lathe. In dry machining, no cutting fluid is used. In flooded and MQL machining, smoothkut SO 7100 soluble oil made by molygraph is used. It is a water soluble metal working fluid having high oil content, fully soluble in water with milky white emulsion, and offers excellent rust and corrosion protection on tools, components and machines and is eco-friendly as it does not contain ozone depleting substances. Typical application of this cutting fluid is diluted with water from 1:16 to 1:20 ratio for general machining. Cutting fluid is flushed in the cutting zone at rate of 5 liters/min and 50 ml/hr in flooded machining and MQL machining respectively. The tool holder used in this work is PSSNR 2525 M12 with SNMG120408 cutting insert (ISO specification).
A total of five process parameters with three levels for each are chosen as the control factors. The five control factors selected are type of machining environment(A), cutting speed (B), feed rate (C), depth of cut (D) and type of carbide tool material (E). The control factors and their levels are shown in Table 1. Selection of particular Orthogonal Array (O.A) from the standard Orthogonal Arrays depend on the number of factors, levels of each factor, interactions and the total degrees of freedom. The five parameters each at three levels have ten degrees of freedom and four two parameter interactions have 16 degrees of freedom. Hence, the total degrees of freedom are 27 which includes overall mean. The required minimum number of experiments to be conducted is 27. Based on this, the 13 nearest O.A. fulfilling this condition is L27 (313) and the factors 13 assigned to L27 (313) O.A. is shown in Table 2.
Titanium specimens are prepared for conduct of the experiments. The specimens are machined on lathe according to experimental design shown in Table 2. The surface roughness is measured on machined specimens using surface roughness tester for each experiment. The summary of mean surface roughness and its Signal to Noise(S/N) ratio are given in Table 2. Optimization of process parameters is carried out with Taguchi's method using Minitab software [10, 13].
In the present work, the performance characteristics namely the surface roughness is to be minimized and hence “smaller the better” quality characteristic has been selected for each of the response [10]. The Signal to Noise (S/N ratio) associated with this response is given in equation (1)
Smaller the better:
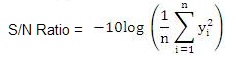
Where, y is the observed data.
Taguchi's robust design methodology has been successfully implemented to identify the optimum process parameters in order to reduce the surface roughness. The mean effect plot for surface roughness is shown in Figure 2. The level of parameter with the highest S/N ratio is the optimal level. It is observed that, the flooded machining environment is found to be optimum as compared to dry and MQL machining conditions and CVD coated tool is found to be optimum as compared to uncoated and PVD coated tools. Thus, the optimal process parameters found are flooded machining (A2), Cutting speed at 114 m/min (B3), Feed rate at 0.2 mm/rev(C1), Depth of cut at 0.6 mm (D1) and CVD coated tool (E2).
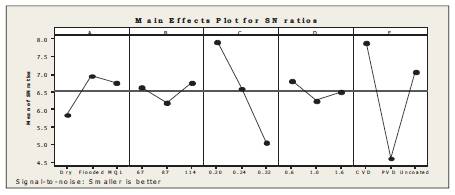
Figure 2. Main effect plots for surface roughness
The S/N ratios of optimum conditions are used to develop predictive or additive model to predict the S/N ratio with optimum condition using equation (2).
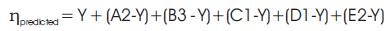
Where Y is average S/N ratio; A2, B3, C1, D1 and E2 are optimum parameters in machining. The predicted S/N ratio is 9.10718 dB, its corresponding surface roughness is 0.35046 μm. The predicted results must be confirmed to the verification test. Hence, the verification experiment is conducted with the optimum conditions, its surface roughness is 0.32839 μm and S/N ratio is (ηexpt) 9.672 dB. It is found that the S/N ratio of the verification test is within the limits of the predicted value at 95% confidence level and significance level of 5%, hence the objective is fulfilled. These suggested optimum conditions can be adopted [10]. It is observed from Analysis of variance (ANOVA) that, individual and interaction between type of machining environment with cutting speed, feed rate, depth of cut and type of tool material are found to be significant. To minimize the surface roughness, CVD coated tool material has major contribution (32.48%) in optimizing the performance characteristics followed by feed rate, type of machining environment, depth of cut and cutting speed.
The prediction of surface roughness (Ra) using regression modelling is developed from data available in Table 2 as given in equation (3).

Where X1 and X2 are qualitative dummy variables for type of machining environment, V is the cutting speed in m/min, F is feed rate in mm/rev, D is Depth of cut in mm, Y1 and Y2 are qualitative dummy variables for type of carbide tool materials. In general, a Qualitative variable with 'n' levels is represented by 'n-1' indicator variables, each taking on the values 0 and 1. Table 3 shows levels of the Qualitative variables for type of machining environment, and tool material by the set of indicator variables [11]. The predicted results for surface roughness are given in Table 4.
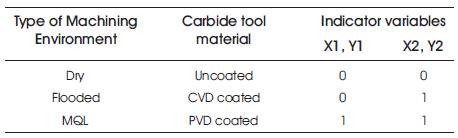
Table 3. Specification of Qualitative variables
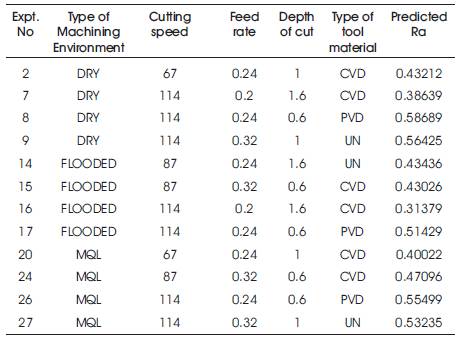
Table 4. Predicted surface roughness values of regression model
An important part of the SA process is the inputs are randomized. The randomization process takes the previous input values and the current temperature as inputs. The input values are then randomized according to the temperature. A higher temperature will result in more randomization; a lower temperature will result in less randomization. There is no specific method defined by the SA algorithm on how to randomize the inputs. The exact nature by which this is done often depends upon the nature of the problem being solved. The Equation (3) has been proposed as the objective function for SA in Matlab. The equations (4a)–(4e) are selected to define the optimization limitations constraints for SA.
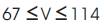
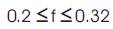
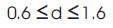

The process parameters that lead to the minimum surface roughness of the regression model would define the optimization initial constraints of SA and are given in equations 5(a) to 5(e):

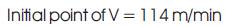


Basically, to obtain the optimal solutions, some criteria must be considered by the SA optimization as listed in Table 5 [7]. The results of the Matlab Optimization Toolbox are given in Figures 3 and 4. The best surface finish obtained under these conditions is 0.382907μm as shown in Figure 3. As seen from Figure 4, it is found that flooded machining, cutting speed at 104.396 m/min., feed rate at 0.2mm/rev., depth of cut at 0.634 mm and CVD coated tool are found to be optimum [10].
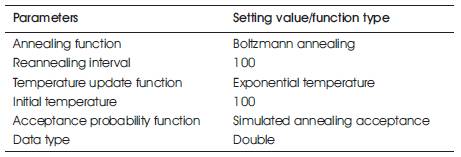
Table 5. Combination of SA parameter rates leading to the optimal solution
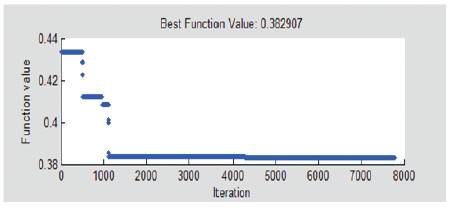
Figure 3. Fitness function plot of SA
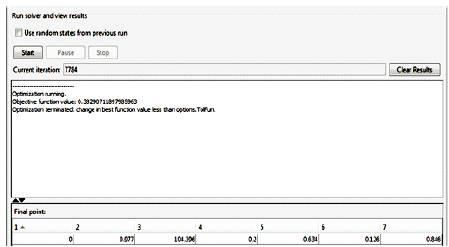
Figure 4. Optimal solution of SA
At the first evaluation, the minimum predicted surface roughness value using predictive model is 0.35046 and the minimum surface roughness value using regression analysis among all the predicted surface roughness is 0.313 μm. Figure 3 shows that the best surface roughness using SA tool is 0.382907 μm. Therefore, the surface roughness obtained from SA is comparable with experimental and regression model. At the second evaluation, the range of cutting parameters selected for experimentation, the optimal cutting conditions obtained from SA are within the range of cutting parameters selected for experimentation. To validate the results obtained from SA, these optimum parameters are substituted in the regression model eq.(4), and the predicted surface roughness value is 0.2716 μm. By referring Table 6, the minimum surface roughness value could be obtained with optimum value from SA if used in the actual machining experiments. Hence, the best surface roughness value is 0.2716 μm using SA optimal parameters with regression equation (3) as shown in Table 6. The Percentage ratio of SA to decrease the surface roughness is calculated. As a result of this analysis, the flooded machining and the CVD coated tool is recommended for use in actual experiments to minimize the surface roughness.
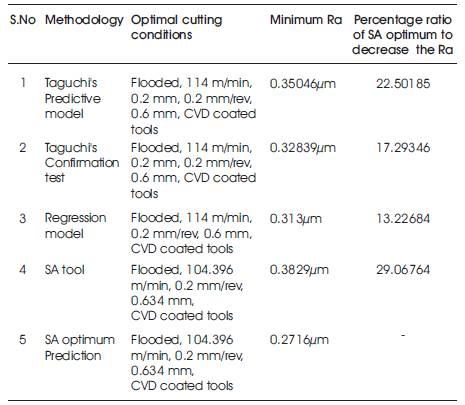
Table 6. Summary of surface roughness results
Based on the results of the present work, the following conclusions are drawn: