Many time endeavors has been devoted to develop a reliable and computationally competent procedure for isomorphism identification in kinematic chains. Many researchers are working in this field for many years, so number of methods is proposed for identification of isomorphism and distinct mechanism by these researchers. Many researchers like Mruthyunjaya (1984), Preben W. Jensen (1991), Rao &Rao (1993), A.C.Rao 2000, Ali Hasan, R.A. Khan and Aas Mohd (2006 ), Mohd, R.A. Khan and V. P. Agrawal (2006), Hasan A., et.al.(2006 a & b), Hasan A., et.al.(2007 & 2008), A. Mohd etc. are doing work in the field of identification of Isomorphism of kinematic chains and its distinct mechanism. But all these methods are taking more time for the identification.

In this paper these methods, such as- Application of link adjacency values by A Dargar (2009), Isomorphism and Inversions of Kinematic Chains Up to 10-Links (Weighted physical connectivity matrix) by Ali Hasan, R.A. Khan, Ashok kumar dargar (2007), Weighted distance matrix by M.K. Lohumi (2008), Joint- Joint matrix by Ali Hasan, Aas Mohd., R.A. Khan (2007), Canonical perimeter topological graph by H. Ding, Z. Huang (2007), Loop based detection method by A. C. Rao (2000), and Distance matrix by J.J. Uicker (1975) are compared from the point of view of following five attributes such as Reliability, Capability, Simplicity Computational time, Computational ease and Structural property. From this rating, it is concluded that the method with the highest total rating may be considered as the best method for isomorphism identification among kinematic chain and their inversions.

There are following attributes on which different methods are compared. These attributes are explained below.

Reliability means, exact solution. It means how correct the method applies to various types of chains, i.e. 6, 8, 9, 10 link chains for single and multi degree of freedom kinematic chains. Reliability of these existing methods may be defined as the percentage of the number of the distinct mechanism of non- isomorphic chains identified by the method out of the total number of distinct mechanism of non-isomorphic chains.

Capability of these existing methods is defined as the ability to perform actions. It means to perform many operations in same time for single and multi DOF, and give result for isomorphism and distinct mechanism both respectively.

Simplicity of these existing methods is defined as how easy to solve this method for the identification of isomorphism and their inversions rather than other existing methods.

Computational time of these existing methods is defined as that how much time is required solving the problem to get the final result of identification of isomorphism and their distinct mechanism. If the calculation is done by computer with the help of any software,. It requires less time while the manual calculation takes more time.

Computational ease of these existing methods is defined as computational ease, as it requires minimum input to get the final results and computation are very easy or user friendly, either manual or using software.

Structural property of these existing methods i.e. the ability of a method to identify various structural properties such as degeneration and type of freedom considering motion of the kinematic chain.

This method, it proposed two invariants called as First Adjacency Chain Link String [FACLS] and Second Adjacency Chain Link String [SACLS]. These invariants take into account the degree of links and type of joints that are used as the composite identification number of a KC. This method is capable of detecting isomorphism in all types of compound KC, i.e. chains of single or multi degree of freedom with simple or multiple joints.

This paper presents a method for the identification of isomorphism and inversions or the Distinct Mechanisms (DM) from a given Kinematic Chain (KC). The method is based on Weighted Physical Connectivity Matrix [WPCM] of the given KC. The two structural invariants namely sum of absolute characteristic polynomial coefficients [WPCMP_] and Maximum absolute value of characteristic polynomial coefficient [WPCMPmax] have been derived and used as the identification numbers of the kinematic chains.

This work presents a new method to identify Distinct Mechanisms (DM) derived from the given family of Kinematic Chains (KC's). KC's and their derived mechanisms are represented in the form of Weighted Distance Matrix [WD] using the graph theoretic approach. Two structural invariants derived from the eigen spectrum of [WD] matrix are the sum of absolute eigen values (WDΣ) and maximum absolute eigen value (WDmax). These invariants are used as composite identification number of a KC and to identify all distinct mechanisms derived from the family of 1-F simple jointed KC's. The identification of distinct KC's and their derived mechanisms is necessary to select the best possible mechanism at conceptual stage of design.

This matrix is based upon the connectivity of the joints through the links and defined, as a square symmetric matrix of size n x n, where n is the number of joints in a kinematic chain.

 

D (λ) gives the characteristic polynomial of [JJ] matrix. The monic polynomial of degree n is given by equation (2).

| (JJ – λ I) | = λⁿ + a₁λ^{n -1} + a₂λ^{n – 2} + --------- a_{n - 1}λ + a_n                                                                   (2)

Where; n = number of simple joints in kinematic chain and 1, a1, a2, an-1, an are the characteristic polynomial coefficients. The two important properties of the characteristic polynomials are

(i) The sum of the absolute value of the characteristic polynomial coefficients (SCPC) is an invariant for a [JJ] matrix. I.e.

| 1 | + | a₁ | + | a₂ | + ----- + | a_n-1 | + | a_n | = invariant

(ii) The maximum absolute value of the characteristic polynomial coefficient (MCPC) is another invariant for a [JJ] matrix.

This work has been done by H. Ding, Z. Huang. This method, is based on graph theory. In this method, the perimeter loop, the maximum perimeter degree- sequence, and the perimeter topological graph, are discussed. Then, based on the perimeter topological graph and some rules for relabeling its vertices canonically, a one-to-one descriptive method, the canonical adjacency matrix set of kinematic chains, is proposed. Another very important characteristic of the descriptive method is that in the canonical adjacency matrix set the element number is reduced dramatically, usually to only one. After that, an effective method to identify isomorphism of kinematic chains is given.

In this method, Structural synthesis of kinematic chains usually involves the creation of a complete list of kinematic chains, followed by a isomorphism test to discard duplicate chains. Using the loop concept, a method is reported in this paper to reveal simultaneously chain is isomorphic, link is isomorphic, and type of freedom with no extra computational effort. A new invariant for a chain, called the chain loop string is developed for a planar kinematic chain with simple joints to detect isomorphism among chains. Another invariant called the link adjacency string is developed, which is a by-product of the same method to detect inversions of a given chain. The proposed method is also applicable to know the type of freedom of a chain in case of multi degree of freedom chains.

In this method the authors present a theorem based on graph theory which leads to a numerical algorithm for testing for isomorphism of two kinematic chains. According to theorem, kinematic equivalent chain may be detected by the equality of these identifying numbers. An extension of the method allows testing the equivalence of chains including different types of kinematic pairs. According to the theorem the topology or connectivity of a kinematic chain is the link-link form of the incidence matrix, more properly referred to as the distance matrix.

The designer at the conceptual stage of design selects the best mechanisms/kinematic chains for the required specific task.

There is an example for comparison between some methods which are given above. To make comparison clear and easy to understand six links one degree of freedom Watt chain and Stephenson chain are shown in Figures1 (a & b) and 2 respectively. We can identify the isomorphism and distinct mechanism of these chain by various methods.

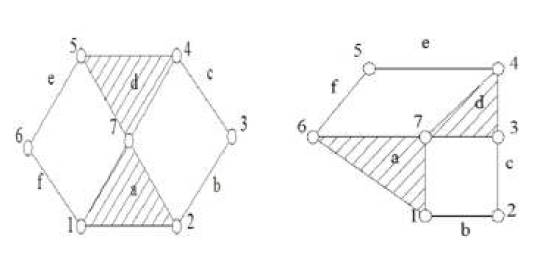
Figure 1(a&b). Watt Chain

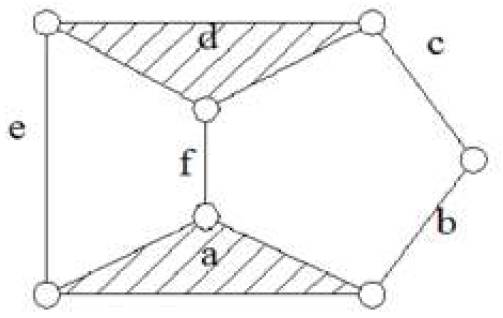
Figure 2. Stephenson Chain

The following definitions are used in this method, i.e. following given below

• Degree of links- a numerical value for the link based on its connectivity to the other links.
• Joint value- the ratio of summation of degree of all the links connected at the joint to the number of links connected at the joint.
  

   

• Link value- the sum of joint values of all the joints of that link.
• First adjacency link value- the sum of link values of all the links that are directly joined to it.
• Second adjacency link value- the sum of first adjacency link values of all the links that are directly joined to it.
• First adjacency chain link string [FACLS]- It is a structural invariant. It is obtained by arranging the FALV of all the links in descending order.
• Second adjacency chain link string [SACLS]- It is also a structural invariant. It is obtained by arranging the SALV of all the links in descending order.

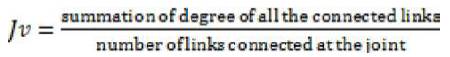
These strings are used to identify the isomorphism of kinematic chain.

For distinct mechanism- observing the structural invariants for the above 6 links it is found that the links are equivalent to the other link, their structural invariants are same so they form distinct mechanism.

• Joint value for (a)- 2.5, 2.5, 2, 2.5, 2.5, 2, 3

  Joint value for (b)- 2.5, 2, 2.5, 2.5, 2, 2.5, 3

  Joint value for (c)- 2.5, 2.5, 2, 2.5, 2.5, 2.5, 2.5

• Link value for (a)- 8, 4.5, 4.5, 8, 4.5, 4.5 Link value for

  Link value for (b)- 8, 4.5, 4.5, 8, 4.5, 4.5 Link value for

  Link value for (c)-7.5, 4.5, 4.5, 7.5, 5, 5

• FALV(a)- 17, 12.5, 12.5, 17, 12.5, 12.5 FALV

  FALV(b)- 17.5, 12.5, 12.5, 17.5, 12.5, 12.5 FALV

  FALV (c)- 14.5, 12, 12, 14.5, 15, 15

• SALV(a)- 42, 29.5, 29.5, 42, 29.5, 29.5 SALV

  SALV(b)- 42.5, 30, 30, 42.5, 30, 30 SALV

  SALV(C)- 42, 26.5, 26.5, 42, 29, 29

Now test for Isomorphism-

• FACLS (a)- 17, 17, 12.5, 12.5, 12.5, 12.5

  FACLS (b)- 17.5, 17.5, 12.5, 12.5, 12.5, 12.5

  FACLS (c)- 14.5, 14.5, 12, 12, 15, 15

• SACLS (a)- 42, 42, 29.5, 29.5, 29.5, 29.5

  SACLS (b)- 42.5, 42.5, 30, 30, 30, 30

  SACLS (c)- 42, 42, 29, 29, 26.5, 26.5

Now, comparing the invariants, in first string for Figures 1 a & b, mostly elements are same. So Figures a & b is isomorphic chain and Figure c is non-isomorphic chain.

For Distinct mechanism- By the observation of first and second string for Figures (a&b), there are two distinct mechanism i.e. there are two equivalent chain a=d, b=c=e=f.

For Figure 2, there are three distinct mechanism and the equivalent chains are, a=d, b=c, and e=f .

There are some parameters which are used in this method.

C: Cylinder lower pair, F: Planer lower pair, G: Spheric lower pair, HP: Higher pairs (point contact), HL: Higher pairs (line contact), P: Prismatic lower pairs, R: Revolute lower pairs, SL: Screw lower pairs

Let R=1.1, P=1.2, C=1.3, SL=1.4, F=1.5, G=1.6, HP=2.1 and HL=2.2. These values are assumed to distinguish the KP.

• Physical Connectivity Matrix [PCM]

  [PCM] {Pij}nxn,

Where, P_ij = Type of kinematic pair between i^th link and j^th link that are directly connected.

=0, when ith and jth links are not connected directly. Off course; P_ii =0

• Degree Vector (V)

d (v_i) =2, for binary link, d (v_i) =3, for ternary link,

D(v_i) = 4, for quarter nary link, d(v_i) =k, for k-nary link.

• Relative Weight of Degree of Vector

W_ij = ½ [v_i/v_j+v_j/v_i]

Here, Vi and vj are the type of ith and jth links connected directly.

• Weighted physical connectivity matrix-[WPCM]= {g_ij}_nxn g_ij =(P_ij) x (W_ij)
• Structural Invariants [WPCMP_] and [WPCMPmax]

[WPCMPå], [WPCMPmax] of [WPCM] matrix are proposed and are obtained by using software MATLAB.

• Tests for Distinct Mechanisms

The mechanisms are obtained by fixing the links of the KC turn in turn. If link 1 is fixed, the diagonal element P11 of [WPCM] is changed from 0 to 1. Then it will be the representation of the first mechanism with link 1 fixed. The structural invariants of [WPCM] matrix of the first mechanism are then calculated. These invariants are the characteristic numbers of the first mechanism. This process is repeated for the second link and so on. In this way, sets of invariants equal to the number of the links are obtained. Some of them are same and others are different. The same structural invariants represent the corresponding structurally equivalent links that constitute one DM.

Let us consider that all joint are pin joint and formed revolute pair.

 

For isomorphism identification, we determine structure invariants with the help of MATLAB software.

• Degree of the Link d(li)

The degree of a link actually represents the type of the link, such as binary, ternary, quaternary links etc. Let the degree of i^th link in a kinematic chain be designated d (l_i)

d(l_i) = 2, for binary link d(l_i) = 3, for ternary link

d(l_i) = 4, for quaternary link d(l_i) = n, for n-nary link

• Shortest Path Distance Matrix

The path between two links i and j is an alternating sequence of links and joints starting from link i and terminating at link j. The sum of the joints in the path is called path length or path distance, the shortest of all the paths is called shortest path distance. The shortest path distance matrix is represented as square symmetric matrix of size n x n, where n is the number of links in a KC.

[D]= {d_ij}_nxn

Where;

d_ij= Shortest path between i^th link and j^th link and d_ii = 0.

• Relative Weight of Degree of Links

The shortest path distance matrix [D] does not provide any information about the types of links existing in a KC. Therefore, this information is included in the [WD] matrix in the form of relative importance of the degree of i^th link and jth link and vice versa. The relative weight of the degree of the links (w_ij) is defined as the ratio between degree of i^th link and j^th link and given as

w_ij = d(l_i) / d(l_j) and w_ji = d(l_j) / d(l_i)

Mutual interactive effect of relative weights is defined as

 

• Interactive Weighted distance Matrix,

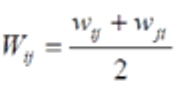
Weighted distance matrix takes the combined influence of shortest path distance between the links and their relative weights. The weighted distance matrix is a square matrix of size n x n and defined as

[WD]= {g_ij}_nxn

Where;

g_ij = {d_ij}x (W_ij).

• Characteristic polynomial of [WD] Matrix

   

The two important properties of characteristic polynomials are

• The sum of absolute eigen values of the characteristic polynomial (WD∑) is constant for a [WD - λ] matrix.
• The maximum absolute eigen value of the characteristic polynomial (WD_max) is also constant for a [WD - λ] matrix.
• Structural invariants (WD∑and WD_max)

These two composite invariants (WD) and (WD_max) are used as the identification number of a KC as well as distinct mechanism derived from a KC.

• Degree of links

  For figure (a)- d(l_a)= (l_d)= 3

  d(lb)= (l_c)=(l_e)=(l_f)= 2

  For figure (b)- d(l_a)= (l_d)= 3

  d(lb)= (l_c)=(l_e)=(l_f)= 2

  For figure (c)- d(l_a)= (l_d)= 3

  d(l_b)= (l_c)=(l_e)=(l_f)= 2

• Shortest path distance matrix representing K.C. of above Figure 2.

 

• Weighted Distance Matrix of above Figure a, b & c respectively

 

• For identification of isomorphism Structural Invariants of Mechanisms

The structural invariants of the above mechanism are derived from the KC shown in Figure1 and 2 and computed as and it has been seen that fig. a and b are isomorphic because their structure invariants are same.

(Wd∑ )1a = 17.6874 (WD_max)1a = 8.7321

(Wd∑ )1b = 17.6874 (WD_max)1b = 8.7321 and

(WD∑ )1c = 15.9220 (WD_max)1c = 7.9610

• For interactive distinct mechanism

Similarly, structural invariants are obtained by fixing links1, 2, 3,…..etc by changing the respective row and column elements to 0 and given as.

For Figure A

(WD∑ )1 = 14.8864 (WDmax)1 = 7.4432

(WD∑ )2 = 13.8118 (WDmax)2 = 6.8221

(WD∑ )3 = 13.8118 (WDmax)3 = 6.8221

(WD∑ )4 = 14.8864 (WDmax)4 = 7.4432

(WD∑ )5 = 13.8118 (WDmax)5 = 6.8221

(WD∑ )6 = 13.81118 (WDmax)6 = 6.8221

For Figure B

(WD∑ )1 = 14.8864 (WDmax)1 = 7.4432

(WD∑ )2 = 13.8118 (WDmax)2 = 6.8221

(WD∑ )3 = 13.8118 (WDmax)3 = 6.8221

(WD∑ )4 = 14.8864 (WDmax)4 = 7.4432

(WD∑ )5 = 13.8118 (WDmax)5 = 6.8221

(WD∑ )6 = 13.81118 (WDmax)6 = 6.8221

For Figure C

(WD∑ )1 = 13.2561(WDmax)1 = 6.6281

(WD∑ )2 = 12.5755(WDmax)2 = 6.2878

(WD∑ )3 = 12.5755(WDmax)3 = 6.2878

(WD∑ )4 = 13.2561(WDmax)4 = 6.6281

(WD∑ )5 = 12.5355(WDmax)5 = 6.2672

(WD∑ )6 = 12.5345(WDmax)6 = 6.2672

By visualization, in the structure invariants of Figure A and B there are two distinct mechanisms. And the equivalent chain of these are a=d, and b=c=e=f.

And in Figure C, there are three distinct mechanisms and their equivalent chains are a=d, b=c and e=f.

 

These matrices are obtained by MATLAB software with help of computational program, and its structural invariants (SCPC and MCPC) are determined.

Structure invariants For Kinematic chain (Figure1 (a, b and c)

*E+003

SCPC -1 MCPC-1 SCPC-2  MCPC-2  SCPC-3   MCPC-3

5.2200  3. 1680  5.2200  3.1680   9.7560   3.6000

Now D.M., Fixing each link of given KC one by one and find equivalent link.

4.5880    2.9440    4.5880    2.9440    0.7196    0.3192

6.3440    3.9510    6.3440    3.9510    0.8032    0.3111

6.3440    3.9510    6.3440    3.9510    0.7196    0.3192

4.5880    2.9440    4.5880    3.9510    1.2280    0.4850

6.3440    3.9510    6.3440    3.9510    1.2280    0.4850

6.3440    3.9510    6.3440    3.9510    0.8032    0.3111

As above results it is clear that KC as shown in Figure 1(a & b) is similar.

And KC (Figure 2) is different.

Equivalent links for Figures1,2 &3 respectively-

KC-1a, 1=4 & 2=3=5=6

KC-1b, 1=4 & 2=3=5=6

KC-2, 1=3, 2=6 & 4=5

There are some parameters which are used in this following method.

Loop of the Topological Graph. A loop or a closed loop consists of an alternating sequence of vertices and edges, where no vertex or edge appears more than once, and every vertex is connected with two edges. Here a loop i is represented as Li .

The Basic Loop. In the topological graph of a kinematic chain, the number L of its basic loops is determined by Euler theorem

L = M − N + 1

Where, N is the number of vertices and M is the number of edges. For a plane topological graph which can be represented by a plane graph, its mesh loops (within which there are no other loops) can be selected as the basic loops.

The Loop Relationship of a Topological Graph. For a topological graph, when its basic loops are determined, all other loops can be obtained through the combination (or “Å ” operation) of the basic loops.

The Maximum Loop. The vertex number or edge number in a loop is defined as the size of the loop, and S [L(i)] is used to represent the size of loop i. In a topological graph, a loop with the largest size is defined as its maximum loop.

The Perimeter Loop. The number of edges connected to a vertex is called the degree of the vertex. The loop degree- sequence is the degree permutation of vertices sequenced one by one from a starting vertex along the loop clockwise or counter- clockwise. Different starting vertices make different degree- sequences, and different directions make different degree- sequences, too. Those degree-sequences can be viewed as numbers. For a loop, the largest number is defined as its canonical degree-sequence.

For a kinematic chain, the largest number of the canonical degree-sequences of all its loops is defined as the maximum perimeter degree-sequence and the corresponding loop is defined as the perimeter loop.

The general procedure for obtaining the perimeter loop

Choose basic loops. The number of the basic loops is determined by Euler theorem. Obtain all loops based on the combinations of the basic loops. All loops of a kinematic chain can be obtained by different combinations of the basic loops. For a kinematic chain with L basic loops, the total number of its loops is TN at most where

 

• Determine the maximum loops. Those loops with the largest size are the maximum loops.
• Determine the perimeter loops. Those maximum loops with the largest canonical degree- sequence are the perimeter loops.

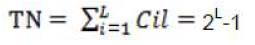
The topological graph can be drawn in many different ways. Here the topological graph for a kinematic chain is drawn as follows:

• Draw the perimeter loop as the outmost loop in the form of an equilateral polygon.
• Put the remaining vertices of the opological graph inside the perimeter loop.

The topological graph drawn in this way is defined as the perimeter topological graph. It consists of two components: one is the perimeter loop and the other is the inner sub chains or sub- chains.

For a perimeter topological graph, relabel the vertices on the perimeter loop first conforming to Rule 1 (The canonical vertex labeling method on the perimeter loop). Then relabel the vertices on inner sub chains conforming to Rule 2 (The canonical vertex labeling on the inner sub chain. In order to relabeling the vertices on inner sub chains canonically, two steps are carried out.

This label is defined as the canonical label and the resulting topological graph is defined as the canonical perimeter topological graph (CPTG).

Two kinematic chains are defined to be isomorphic if there is a one-to-one correspondence between the links of one chain and those of the second chain, such that two links of the chain are joined by a kinematic pair if and only if the corresponding links of the other chain are also joined by a kinematic pair. If there is no such correspondence, the two chains are non-isomorphic.

Theorem 1: . For any two kinematic chains A and B, if the intersection set of their adjacency matrix sets are not empty [1], then these two chains are isomorphic.

AMS(A) η AMS(B) ≠ Φ

AMS- Adjacency Matrix Set

Note: But there are too many elements in the AMS, so the theorem is difficult to use. Now with the canonical adjacency matrix set of kinematic chains, the problem can be solved more easily.

Theorem 2: For any two kinematic chains A and B, if and only if the canonical adjacency matrix sets of the two kinematic chains satisfy. The two kinematic chains are isomorphic;

CAMS(A) η CAMS(B) ≠Φ

CAMS- Canonical Adjacency Matrix Set

Note- By the canonical perimeter topological graph of a kinematic chain, the elements in the adjacency matrix set are greatly reduced. Figures 3 (a & b) and Figure 4 are developed by the graph theory. These figure came here from Figure 1 and 2 (given Watt and Stephen chains).

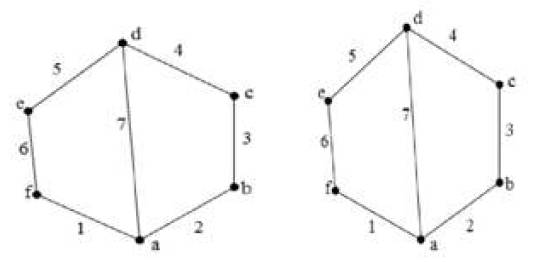
Figure 3. Canonical topological graph of k.c 1 (a) and (b)

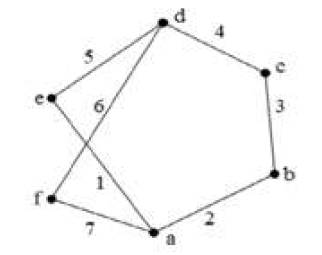
Figure 4. Canonical topological graph of K.C.

The total rating of the above six methods are based on comparison from above six attributes such as Reliability, Capability, Simplicity Computational time, Computational ease and Structural property are shown in following Table 1.

Table 1. Comparison between given methods

This is empirical analysis and this ranking is hypothetical. And it can vary from the vision of author. This analysis is based on above mentioned parameters. And according to these parameters joint-joint matrix by computational program is very easy to understand and taking less time to identify isomorphism and its inversion. It is fully computational work, and the software is user friendly.

Here, Loop based method is also based computational program, but it is not easy to understand but according to above mentioned category it is highest ranking so this is the best method but Joint- Joint Matrix method for the identification of isomorphism and distinct mechanism is the second best method for the identification of isomorphism because it has user friendly computational function.