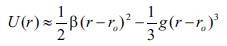
The modulus of elasticity is one of the most important mechanical properties of a material. It needs to be determined accurately in order to facilitate mechanical design, ensure reliability and promote compliance with legislative restrictions. The modulus-temperature relationship is traditionally determined experimentally, and the procedure is time consuming, expensive, and often impossible. The main goal of this work is to obtain a comprehensive analytical relationship between modulus of elasticity and temperature, based on the kinetic nature of the strength of solids and a nonlinear equation of state for materials. The analytical modulus-temperature relationship is compared with existing experimental data. Results demonstrate the potential of the nonlinear approach to predict the static and dynamic elastic modulus of different engineering materials (metals, plastics, and concrete) as a function of temperature.
Engineering materials are subject to forces when they are used in a structure. Mechanical engineers need to calculate those forces and design the structure to meet engineering specifications. Materials deform (elongate, compress, twist, or break) as a function of applied load, temperature, time, and other conditions. Material scientists investigate these mechanical properties by testing materials using common standards or procedures such as those published by the American Society for Testing and Materials (ASTM).
Temperature-dependent material properties are very important for the analysis of materials in an environment with changing temperatures. In a Finite Element Analysis (FEA), for instance, this would require an analyst to input material properties in the form of tabulated data for different temperatures. These material data are often experimental, difficult to obtain, prone to error and tedious to input. Because the experimental data are scattered, some approximations have to be introduced to smooth the data. This introduces errors and often causes difficulties in achieving a converged solution in a numerical analysis. One of the more important mechanical properties, the modulus of elasticity or Young's modulus, is sensitive to both temperature and rate of loading, i.e., the stress or strain rate. The modulus-temperature relationships, E(T), of different engineering materials are always determined experimentally. A well-validated theoretical basis for predicting the modulus of elasticity of engineering materials within certain temperature ranges would be a valuable alternative to the traditional time-consuming, expensive, and very often impossible empirical methods. The establishment of such a relationship between the modulus of elasticity and temperature for engineering materials would help engineers and designers accurately capture the material behaviors before deformation becomes inelastic or during unloading when the material tends to return to its original configuration elastically.
The need for a well-validated analytical relationship between the modulus of elasticity and temperature for engineering materials is demonstrated, in part, by the following considerations
The major objective of this work is to establish the validity of a comprehensive theoretic model for predicting the relationship between modulus of elasticity and temperature for a wide spectrum of engineering materials: metals, plastics, and concrete.
The theoretical "modulus of elasticity-temperature" relationship is based on the nonlinear (quadratic) "stress-strain" dependence for industrial materials and the kinetic nature of the strength of solids (Bell 1983; Regel et al.1974).
In general, this relationship follows from the diatomic model of a solid body (Frenkel 1946; Layus et al. 2004), which shows that the nonlinear approximation of the potential energy of two atoms as a function of the distance between them adds an asymmetric cubic term to the potential
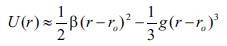
where β is the coefficient of linear elasticity, g is the anharmonic coefficient, r0 is the distance between atoms at the equilibrium position, and r is the instantaneous distance between two atoms.
If the potential energy of two atoms is a parabola, then the interaction force between the atoms, F, is proportional to the displacement from equilibrium, r- r0: F= dU/dr = β r - r0), or F/r02 = Eo(r-r0 )/r0; where Eo = (β/r0 ) is the modulus of elasticity. It is important to point out that in this case the atoms oscillate harmonically, the values of energy at negative and positive displacement are equal, and the distance between atoms does not change with temperature.
The cubic term in Eq.(1) leads to asymmetry of the potential energy. In comparison with parabolic potential, the curve of potential energy is flatter at positive displacements and steeper at negative displacements. The resulting decrease in potential energy for positive displacement leads to expansion of the material, a shift of the center of anharmonic thermal oscillations, and softening of the mechanical properties of the solid. In particular, the modulus of elasticity decreases linearly with linear thermal expansion (Frenkel 1946; Layus et al. 2004).

where E(T) is the modulus of elasticity at temperature T, Eo is the modulus of elasticity at the reference temperature To, g is the anharmonic coefficient, and α is the coefficient of linear thermal expansion. Equation (2) indicates the general trend: the modulus of elasticity decreases as the temperature increases. For common structural materials the anharmonic coefficient g is often of the same order of magnitude as E0 (Frenkel 1946. If g = 0, the effect of temperature vanishes. Thus, in the diatomic model of a solid body the value of the modulus of elasticity at different temperatures is defined by Eq. (2) and depends only on the asymmetry of the interatomic forces, represented by g. However, the diatomic model does not take into account the influence of impurities, defects, and the time (or rate) of loading.
Numerous experimental results available at present indicate that the modulus of elasticity and nonlinear deformation of real materials are affected much more by micro- and macrostructure features (dislocations, micropores, microcrevices), the stress/strength ratio, and stress (or strain) rate of loading than by asymmetry of interatomic forces. The data (Bell 1983) show that the change of the modulus of elasticity can not be caused only by the change of density of a material due to thermal expansion.
It is also important to point out that the mechanism of fracture is a change in the thermal movement of atoms (Regel et al.1974). According to the kinetic theory of the strength of solids, fracture is a strain (stress) rate dependent phenomenon (Regel et al.1974). At the atomic-molecular level the fracture process is controlled by the breaking of interatomic bonds due to thermal fluctuations. At the macroscopic level the fracture of stressed solid proceeds by a process that begins to develop in the body from the moment a load is applied and the fracture itself is the final act in this process.
Indeed, with thermal vibration the material is a dynamic system of atoms interacting with external forces, rather than a static system. The thermal pressure caused by inter-atomic vibrations can be estimated as (Frenkel 1946
where k = 1.38•10-23 J/oK is Boltzmann's constant and Wa ≈ 10-29 m3 is the volume of an atom.
This thermal pressure leads to an equivalent stress of elastic forces and increases the local stress between atoms. A rough estimate illustrates that vibration of atoms with average kinetic energy causes load 'jerks' on the atomic bonds with stresses of the same magnitude as the strength of engineering materials(Regel et al.1974). For example: if g/Eo ≈ 1 and T = 298 K, then kT = 411•10-23J ≈ ( 2.5 kJ/mol), and the thermal pressure is P ≈ 206 MPa.
Thermal fluctuations of energy, exceeding the average energy of atoms, depend on time of test, have an essential influence on the structure of real materials and predetermine their behavior under loading. In accordance with the kinetic nature of strength (Regel et al. 1974; Betekhtin et al. 1994) , the fracture is the result of a process of nucleation, accumulation, and development of damage elements, i.e., it is a time-dependent phenomenon. It has been shown (Betekhtin et al. 1974) that the strength of different solid materials, sr, depends on the temperature and rate of loading according to the relation
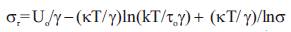
where Uo is the initial dissociation energy of the interatomic bonds of the solid, γ is a structurally sensitive coefficient (given below) (Regel et al. 1974); τo~ 10-13 seconds is the period of inter atomic vibration, and σ is the stress rate of loading. Also, according to the kinetic theory of solid strength the linear extrapolation of the dependence σr(lnσ) to σr=0 leads to a certain value of ln( σo ) which can be estimated (Regel et al. 1974);; Betekhtin et al. 1994) as
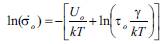
Then Eq. (4) becomes
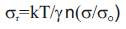
Typical values of γ are 0.84~4.01 kJ•mol-1•MPa-1 for metals and 0.06~0.39kJ•mol-1•MPa-1 for polymers (Regel et al. 1974). From Eq. (5) it follows that the dependencies on τo and γ are logarithmic (small in comparison with linear dependency on Uo). Thus, ln( σo ) is determined essentially by the activation energy Uo of the solid. Therefore, knowing the values of kT, τo, and the level of activation energy Uo, ln( σo ) can be estimated as
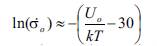
Dynamic and quasi-static experiments show a nonlinear dependence between stress and strain even at infinitesimal values of deformation (10-4 ~ 10-6) for a wide range of materials (metal, stone, concrete, wood, glass, polymers, etc.). Engineering materials deviate from Hook's law, and the stress-strain relationship may be approximated by a second-order Taylor series polynomial

where σ is stress, ε is strain, Eo is the elastic modulus and b is the nonlinear parameter (Bell 1983) (Bell 1983). Equation (8) illustrates that the modulus of elasticity is linearly proportional to the strain
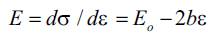
The corresponding value of the nonlinear parameter "b" can be written as
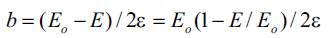
For a uniform distribution of external load, all inter atomic connections are strained equally, and the average stress σ acting on the body is equal to the stress σa acting on the atom. Under the action of stress σa, which is less then the ultimate value, the potential energy U(σa) is proportional to the volume of atom (Wa), and in accordance with equation (8) becomes (Shkolnik 2006, 1996; Shkolnik and Cameron 1996).
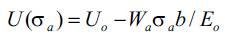
Since the potential energy decreases linearly with applied stress as according to (Regel et al. 1974)
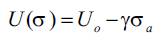
From equations (11), (12) and (6) it follows that
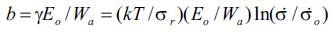
Consequently, from equations (8) and (13), the equation of state is

and the relationship between modulus of elasticity E and temperature T is
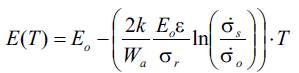
Equations (14) and (15) are generally applicable for all solids that obey the kinetic theory of strength and that can be described with a parabolic stress-strain relationship. Thus, we put forward a hypothesis which unites the non-linear stress-strain relationship of engineering materials with the kinetic approach to the strength of solids (Bell 1983; Regel et al.1974).
Of course from the practical point of view, the right hand side of Eqs. (14) and (15) depends on the known standards for solids (ASTM Standard E8 2009; ASTM Standard E111 2004; ASTM Standard D638 2008), that is mechanical properties of specimens at a given reference temperature (typically 25°C): elastic modulus Eo, strength σr (tensile or compressive), corresponding strain ε, and stress rate of loading σs and σ0.
Equation (15), as mentioned above, indicates the dependence between modulus and stress (strain) rate of loading. But the temperature dependence is linear while the stress (strain) rate dependence is logarithmic. Since the linear temperature dependence is stronger, we investigate here first the validity of the temperature dependence predicted by Eq. (15). Before making a rigorous comparison between Eq. (15) and the published data, we note that all the references (Fabco Plastics 2007; NIST ; Cheng and Siewert 2003; Shkolnik et al. 2008; Syed 2004) show that for different engineering materials the relationship between Young's modulus and temperature is essentially linear, consistent with Eq. (15).
The authors present a detailed theoretical scheme to estimate the dependence between modulus of elasticity and temperature, then we use two very different engineering materials - ductile materials (solders, plastics) and brittle materials (concrete) - to illustrate the possible breadth of the theory. A benefit of disseminating this theory to the research community, along the sample cases presented here, is to allow experimental investigators to compare their data with the theory and encourage them to publish the relevant tests conditions (that are needed for applying the theory) along with their data.
Existing published data (Fabco Plastics 2007; NIST ; Cheng and Siewert 2003; Shkolnik et al. 2007; Syed 2004) are used first to test the hypothesis that Eq. (15) describes in general the relationship between modulus of elasticity and temperature for metallic materials (steels, copper and copper alloys, nickel and nickel alloys, titanium, aluminum and aluminum alloys). Figure 1 depicts the experimental data of modulus of elasticity versus temperature for ten different metals (Fabco Plastics 2007). From Eq. (15) it follows that
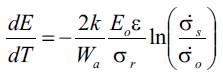
The slopes (dE/dT) and correlation coefficients for metallic materials are tabulated in Table 1. It is shown that the correlation coefficients range from -0.945 to -0.998, indicating very good linear relationship between modulus of elasticity and temperature for these materials. The modulus of elasticity decreases progressively with increasing temperature (Figure 1), that is, the slope dE/dT is negative, and the relationship is essentially linear (note the proximity of the correlation coefficient to -1 in corresponding ranges of temperature) for all metals.
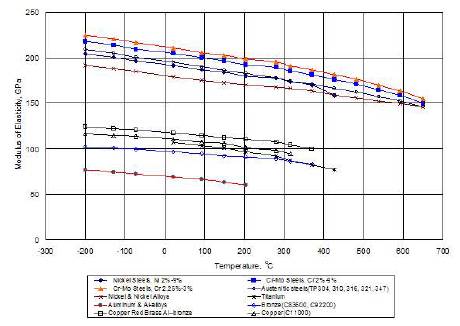
Figure 1. Modulus of Elasticity vs. Temperature for Metals
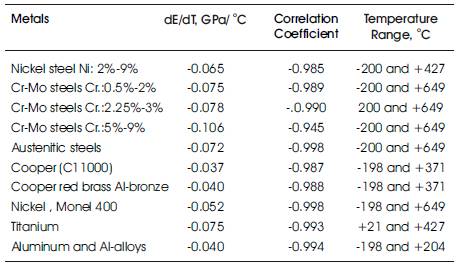
Table 1.Existing Experimental Data for Metals (Fabco Plastics 2007)
The parameter values needed for the theoretical expression are available in the standards and literature (ASTM Standard E8 2009; ASTM Standard E111 2004). Therefore, published data were used also to check if Eq. (15) predicts the absolute values of modulus of elasticity for different temperatures. For instance, the modulus of elasticity of lead-free solders is a key material property that needs to be measured accurately in order to facilitate design, ensure reliability, and promote compliance with legislative restrictions on hazardous substances (NIST).
Here we cite data for the lead-free solder 96.Sn-3.5Ag (Cheng and Siewert 2003; Shkolnik et al. 2007; Syed 2004)
Figure 2 shows the comparison between theory, Eq. (15), and experimental data for three solders: as-cast #1, as-cast #2 and aged #1 (NIST ; Shkolnik et al. 2007). Because the necessary test parameters were known, the differences between the theoretical and experimental values of the elastic modulus for the cases shown in Figure 2 are less than 4% at all temperatures, which is within the range of experimental error. The theory matches the published data reasonably well.
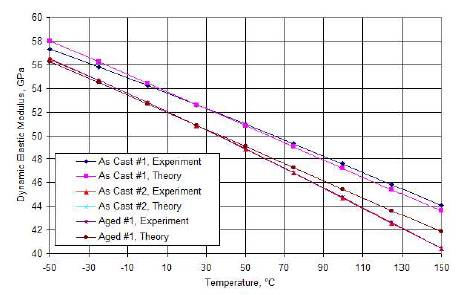
Figure 2. Comparison of theory, Eq. (15), and experimental data for three SnAgCu solders (Cheng and Siewert 2003; Shkolnik et al. 2007)
A natural next step is to determine the values of the correlation coefficients for different plastics at different ranges of temperature. Comparisons also show agreement between the theoretical modulus-temperature relationship and existing experimental data for plastics (ASTM Standard D638 2008) such as Elastollan Polyester C85A (Figure 3), Celcons M90 and GC25 (Figure 4), Polyethylene-HDPE (Figure 5), Chlorinated Polyvinyl Chloride-CPVC, and Polyvinylidene Fluoride-PVDF (Figure 6 and Table 2).

Figure 3. Modulus of Elasticity vs. Temperature for Elastollan Polyester (Fabco Plastics 2007)
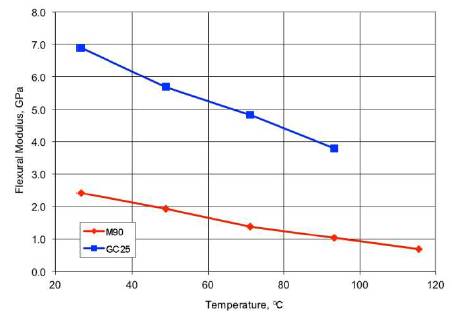
Figure 4. Modulus of Elasticity vs. Temperature for Celcons (Fabco Plastics 2007)
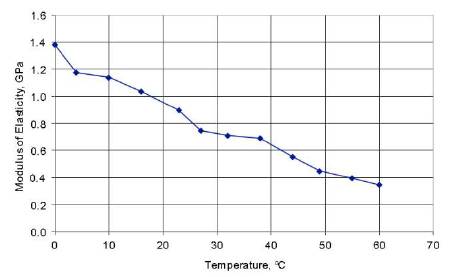
Figure 5. Modulus of Elasticity vs. Temperature for HDPE pipe (Fabco Plastics 2007)
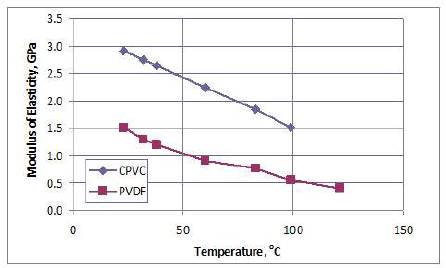
Figure 6. Modulus of Elasticity vs. Temperature for Plastics (Fabco Plastics 2007)
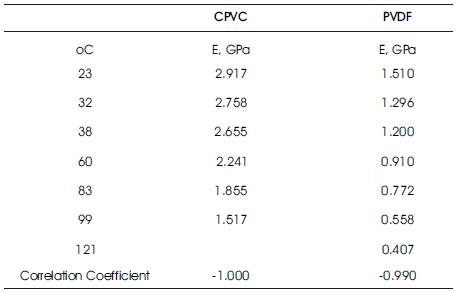
Table 2. Existing Experimental Data for CPVC and PVDF (Fabco Plastics 2007)
Table 3 illustrates the values of slope (dE/dT) for these plastics. It can be seen that the values of the slope (dE/dT) are different for different materials and, consequently, depend on corresponding mechanical properties (e.g. modulus of elasticity at room temperature, strength, and activation energy) and on the test conditions (e.g. stress or strain rate of loading), which is in agreement with Eq. (15). Similar to the metals, the correlation coefficients range from -0.950 to -1.000, indicating good linear relationship between modulus of elasticity and temperature for these plastics. It suggests that it is possible to predict the modulus of elasticity at different temperatures using the mechanical properties of plastics at standard test conditions.
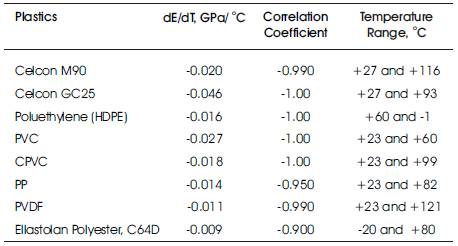
Table 3. Existing Experimental Data for Plastics (Fabco Plastics 2007)
Figure 7 shows the experimental data of modulus of elasticity at different temperatures for four concrete mixtures (Phan and Carino 2002). It is seen that the modulus of elasticity decreases approximately linearly with the temperature increment. According to thermal properties, Eq. (2), and the kinetic nature of strength of solid materials, the "modulus of elasticity-temperature" relationship, Eq. (15), can be expressed as (Shkolnik 2005)
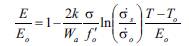
where E is the modulus of elasticity at the in situ temperature (T), Eo is the modulus of elasticity, and f ’0 is the strength of concrete specimens; both Eo and f ’0 are at the reference temperature To (typically room temperature).
To determine the relative value of static modulus of elasticity at elevated temperatures, Eq. (17) requires the stress/strength ratio and the stress rate of loading. According to ASTM C469 (ASTM Standard C469-02e1 2002), σ/f ’0= 0.4 and σS = 0.24 MPa/s.
Using these values for the test parameters the ratio of modulus of elasticity can be calculated as

or

The different slopes for the temperature range 100 °C £ T £ 600 °C and 100-450 °C are due to the different values of In(σ0) at Uo ≈430 kJ•mol-1 (Shkolnik 2005), Eq.(15), in the test procedures.
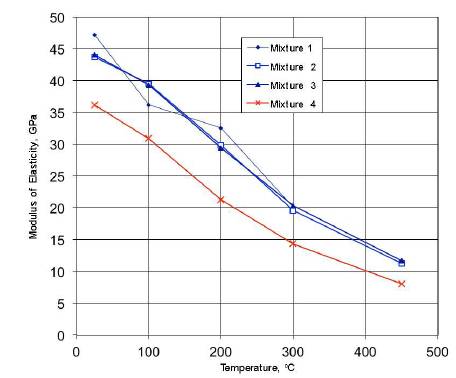
Figure 7. Modulus of Elasticity vs. Temperature for Concrete (Phan and Carino 2002)
Tables 4 & 5 show experimental results for stressed tests with silica fume (mixture I: water-cement ratio w/c = 0.22, f ’0= 98 MPa; mixture II: w/c = 0.33, f ’0= 88 MPa) (Phan and Carino 2002). Tables 6 & 7 give experimental results of unstressed tests for concrete without silica fume (mixture III: w/c = 0.33, f ’0= 75 MPa), and with silica fume (mixture II) (Phan and Carino 2002). The average slope of the elastic modulus in the temperature range 100-450 °C is -0.079. In all cases, as shown in the tables, the "relative static elastic modulus-temperature" dependencies are similar; they are all approximately linear (correlation coefficients close to -1.000), which shows good correspondence to the general analytical model presented here.
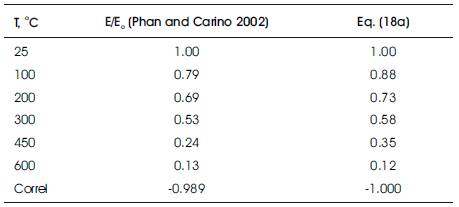
Table 4. Relative Static Modulus of Elasticity Mixture I, Stressed tests, Eo = 45 MPa
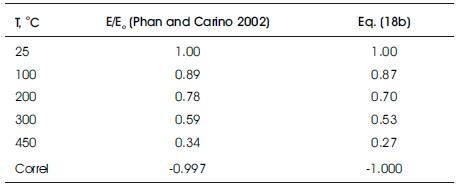
Table 5. Relative Static Modulus of Elasticity Mixture II, Stressed Tests, Eo = 42 MPa
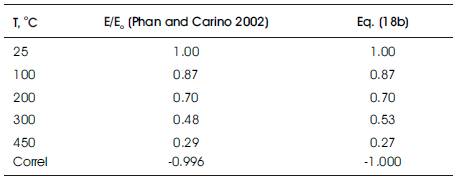
Table 6. Relative Static Modulus of Elasticity Mixture III, Unstressed Tests, Eo = 43 MPa
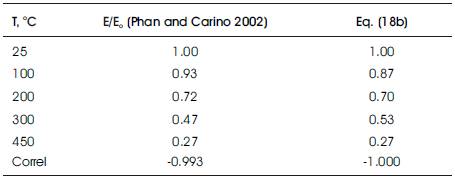
Table 7. Relative Static Modulus of Elasticity Mixture II, unstressed tests, Eo = 42 MPa
The tests for residual dynamic modulus of elasticity were performed by NIST at room temperature (before and after heating) in accordance with ASTM C215 (ASTM Standard C215 2008).
Figures 8, 9, and 10 show that the relative residual dynamic modulus of elasticity decreases approximately linearly with temperature. The error between the predicted, Eq. (18b), and experimental values does not exceed 15% in the temperature range 100-450 °C (except Mixture IV at 450 °C).
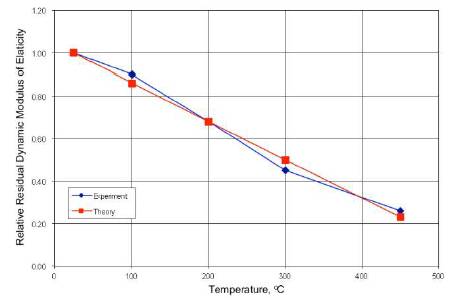
Figure 8. Relative Residual Dynamic Modulus of Elasticity vs. Temperature (Mixture II)
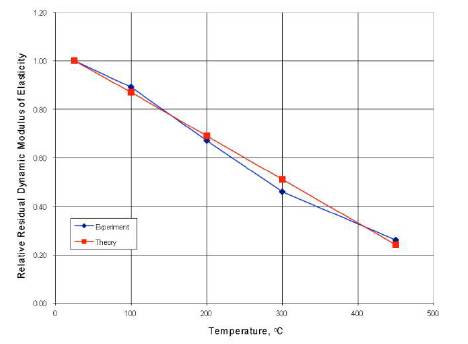
Figure 9. Relative Residual Dynamic Modulus of Elasticity vs. Temperature (Mixture III)
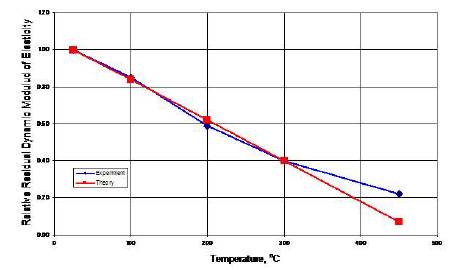
Figure 10. Relative Residual Dynamic Modulus of Elasticity vs. Temperature (Mixture IV)
Strength, modulus of elasticity, and ultrasonic pulse velocity of concrete all decrease with increasing porosity (Phan and Carino 2002). Elevated temperature causes damage and increases porosity. This effect of temperature provides the physical background for estimating the mechanical properties of concrete at elevated temperature.
The modulus-temperature relationships of industrial materials are always determined experimentally. As an alternative, a new analytical relationship between elastic modulus and temperature is presented. The resulting expression, Eq. (15), is based on parabolic stress-strain dependence and the kinetic nature of strength of solids. Preliminary comparisons with existing experimental data provide promising results.
These results indicate that the modulus of elasticity at different temperatures can be predicted by Eq. (15) using well-known physical constants and the mechanical properties of each material only at room temperature (in accordance with existing test standards).
The theoretical E(T) model developed in this work can change the traditional experimental approach for obtaining one of the most important material properties, modulus of elasticity at different temperatures. The model presented here has the potential to eliminate a lot of time consuming and costly material testing and to benefit material engineers and scientists greatly in analytical and design work.
This E(T) model may significantly enhance and facilitate analysts in material engineering and manufacturing process simulations because the validity of the simulation results depends strongly on the inputs of the material properties. From the simulation, the temperature distribution is predicted, and this E(T) model will allow the theoretical prediction of E. It will allow designers to improve the performance and reliability of parts by knowing how their properties will vary over different operating temperatures.
For materials and locations where it is difficult to experimentally measure the modulus of elasticity, the E(T) model may provide a reliable and convenient way to predict modulus at different locations such as on the surface and inside the part.
The authors wish to thank the Kettering University Department of Mechanical Engineering for providing partial funding for this research.
| E | modulus of elasticity at instantaneous temperature, T |
| Eo | modulus of elasticity at reference temperature, To |
| F | force |
| fo' | strength of concrete specimens at the reference temperature |
| g | anharmonic coefficient |
| k | Boltzmann's constant |
| P | thermal pressure |
| r | distance between atoms |
| r0 | the distance between atoms at equilibrium position |
| T | temperature |
| To | reference temperature |
| Uo | activation energy of the solid |
| U(r) | potential energy as a function of distance |
| Wa | volume of an atom |
| α | coefficient of linear thermal expansion |
| β | coefficient of linear elasticity |
| ε | strain |
| γ | structural sensitivity coefficient |
| σ | stress |
| σr | strength |
| σs | stress rate |
| σ0 | the approximation of stress rate as a result of extrapolating the value of strength to zero |
| τ0 | the period of interatomic vibration |