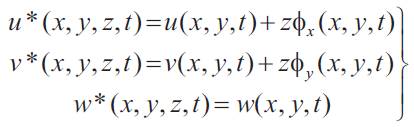
A finite element model, based on first-order shear deformation theory, is used in this study for the free vibration analysis of laminated composite plates. In this paper, the free vibration analysis of laminated composite plates are studied for different support conditions, aspect ratio, lamination scheme, material anisotropy, span to thickness ratios and stacking sequences. It is revealed that the first-order shear deformation theory provides reasonably dependable results for natural frequencies of laminated composite plates. The good agreement with other methods demonstrates the validity and the reliability of the proposed method.
The vibration analysis of plates has been studied extensively by researchers using various numerical methods. The development of numerical approaches has led the invention of some important methods, including Ritz method, finite difference method (FDM) etc. Although these methods have demonstrated efficiency and accuracy in solving plate problems, there are still some limitations in engineering applications. In Ritz method, it is difficult to choose the appropriate trial functions for complicated problems; the FDM is more flexible than the Ritz method, but requires a set of ''structured'' grids, which limits its application for problems of complex geometry. The FEM is so far the most flexible and effective numerical technique developed in recent years.
The analysis of natural frequencies of composite plates/shells plays an increasingly important role in the design of structures in mechanical, civil and aerospace engineering applications. Great progress has been made over past decades towards better understanding of the vibration characteristics of laminated composite plates/shells [1-3]. Due to limited availability of analytic solutions for practical applications, numerical approximate methods have become the most effective tools. The finite element method (FEM) is considered to be a very effective and versatile approach for these problems. There is a vast amount of literature on free vibration analysis of laminated plates/shells which is too large to list here. Bert [1] and Mohamad [2] have conducted surveys and provided details on the development of the finite element methods for modeling and modal analysis of laminated plates/shells. Further extensive references on shells can be found in the excellent review of Yang et al. [3]. Dynamic Mechanical Properties of Fibre Reinforced composite Materials and Structures is studied by Gibson [4]. Results for fundamental frequency of symmetric cross-ply laminated plates were presented by Khdeir [5], using an 'exact' analytical method. A finite element model, based on third-order shear deformation theory, is presented by Latheswary et al. [6] for the linear and the non-linear free vibration analysis of laminated composite plates. The free vibrations characteristics of simply supported anisotropic composite laminates are investigated by Ganapathi et al. [7] using analytical approach. The formulation is based on the first-order shear deformation theory and the shear correction factors employed are based on energy consideration that depends on the layup as well as material properties. The governing equations are obtained using energy method. Linear static analysis and finite element modeling for laminated composite plates using third order shear deformation theory is studied by Rastgaar [8]. In this paper, deformations of a laminated composite plate due to mechanical loads are presented. Third order shear deformation theory of plates, which is categorized in equivalent single layer theories, is used to derive linear dynamic equations of a rectangular multi-layered composite plate. Taylor et at. [9] developed the analysis and numerical calculations for the exact free vibration characteristics of simply supported, rectangular, thick, multilayered composite plates and assumed that each layer of the composite plate is of arbitrary thickness, is perfectly bonded to adjacent layers, possesses up to orthotropic material symmetry and that its material crystallographic axes are oriented either parallel or perpendicular to the plate's boundaries. The analytical solution to the free vibration response of rectangular plates with arbitrary lamination, using first-order shear deformation theory, has been presented by Kabir [10]. Liew [12] solved the vibration of thick symmetric laminates by Reissner/Mindlin plate theory and the p-ritz method with various combinations of boundary conditions, to incorporate the effects of transverse shear deformation and rotary inertia, first-order Reissner/Mindlin plate theory is employed. A small deflection, thin, layered composite plate analysis, based on a modified shear deformation theory and using Rayleigh-Ritz energy approach, has been presented by Kamal et al. [13]. A higher-order shear deformation theory is used to determine the natural frequencies and buckling loads of elastic plates by Reddy et al [14].
A review of the recent development of the finite element analysis for laminated composite plates from 1990 is presented by Zhang et al. [15]. Kant et al. [16] studied a refined higher-order theory for free vibration analysis of un-symmetrically laminated multilayered plates. A four-noded rectangular element with seven degrees of freedom at each node is developed by Ghosh et al. [17] for the vibration analysis of laminated composite plate structures having a constant thickness of any individual layer. Large amplitude free vibration of orthotropic plates was studied by Ambartsumyan [18]. Analytical and finite-element solutions of the classical, first-order, and third-order laminate theories are developed by Reddy and Khdeir [20] to study the buckling and free-vibration behavior of cross-ply rectangular composite laminates under various boundary conditions. Generalized Levy-type solutions are obtained by Hadian and Nayfeh [21] for the problems of linear vibration and stability of cross-ply laminated plates. The Ritz method with algebraic polynomial displacement functions is used to solve the vibration problem for laminated composite plates having different boundary conditions by [22].
Based on the previously outlined literature, it is clear that the behavior of composite plates subjected to free vibration was not established since none of the approximate or the exact solutions obtained covered all possible boundary conditions, geometric factors. Hence, this paper aims at utilizing the finite element method in order to
i)Find the natural frequency of symmetrically laminated and fibre-reinforced composite plates of various boundary conditions and comparing obtained results with those in the literature.
ii) Study the effect of fibre orientation on the natural frequency.
Consider a rectangular plate having the lengths of a and b and a constant thickness of h. The co-ordinate system (x, y, z) chosen is placed at the middle of the plate and the co-ordinate parameters are such that -a/2 ≤ x ≤ a / 2, -b / 2 ≤ y ≤ b / 2, and - h /2 ≤ z ≤ h / z. The plate is assumed to be constructed of arbitrary number, N, of linearly elastic orthotropic layers. Hence, First-order shear deformation plate theory (FSDT) makes the same assumptions as those made for a thick isotropic plate. That is, referring to Figure 1 shows the geometry of a laminated rectangular plate made up of orthotropic layers. Considering the first order shear deformation theory, the displacement fields are expressed as follows [19].
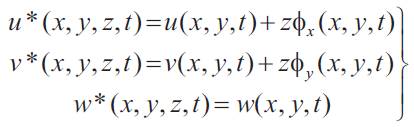
The strain displacement relations can be expressed as follows. In-plane strains at the mid-plane are:

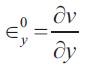
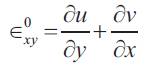
The curvatures are:
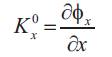
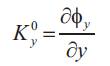
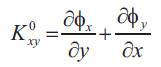
The shear strains in xz and yz planes are:
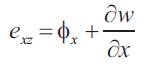
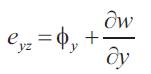
The constitutive equations are
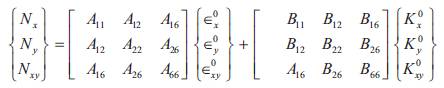
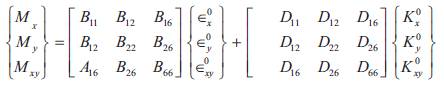
Aij is referred to as the in-plane (stretching and shearing) stiffness matrix and is termed as the in-plane stiffness coefficient of the laminate. They are independent of the stacking sequence of the laminate.
Bij is the coupling stiffness matrix. The terms are the coupling terms which relate the in-plane forces to curvatures and moments to in-plane strains. The elements are called the coupling stiffness coefficients of the laminate.
Dij is the out-of-plane (bending and twisting) stiffness of the plate. The terms are bending stiffness terms which relate moments to curvatures. The elements are the bending stiffness coefficients of the laminate. They are strongly dependent on the stacking sequence of the laminate.
ABD matrix is symmetric and so A and D is also symmetric. However (unlike the case of a laminated plate) in general B is not symmetric.
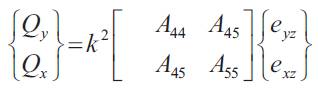
Where, for an n-layered (k = 1, 2,….n) plate,
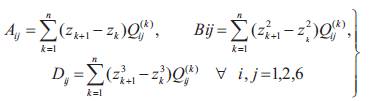
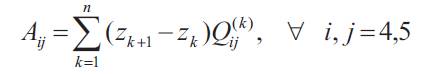
The stiffness constants for Q(k)ij the kth layer are
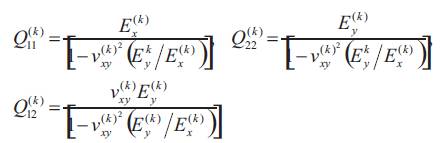
For the cases of symmetric and antisymmetric cross-ply laminated plates made up of orthotropic layers
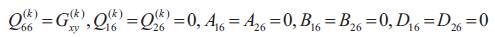
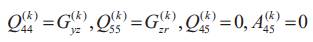
Equations of motion in terms of stress resultants and non-dimensional coordinates can thus be derived using the principle of virtual work as, [19]
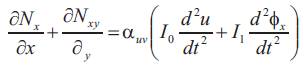

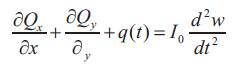
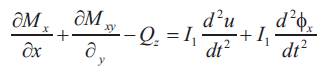
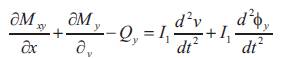
The inertias are defined as follows
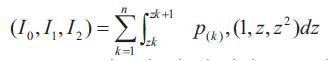
Since every laminated plate considered in this work has symmetry in terms of density about the mid-plane (z = 0), the inertia component I1 is always zero.

Figure 1. Laminated Composite Plate
Here all layers of the laminated plates are of the same thickness, and made of the same material. The effect of various parameters like width-to-thickness ratio, material anisotropy, fibre orientation, aspect ratio, edge conditions and number of layers on the fundamental frequency of vibration is studied by considering the laminated plates of side 250 mm and having the following non-dimensional properties.
E1/E2 = 40; E2 = E3
G12 = G13 = 0.6E2; G23 =0.5E2
ν12 = ν13 = 0.25; ν23 =0
The numerical computations are performed by using a personal computer with double precision. In all of the numerical results presented, the frequency parameter is taken as 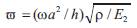 . As an initial application of the present shear deformable plate theory, the free vibration frequencies are obtained for symmetric and antisymmetric square (a=b) cross-ply plates subjected to different boundary conditions and compared with the ones available in the literature.
. As an initial application of the present shear deformable plate theory, the free vibration frequencies are obtained for symmetric and antisymmetric square (a=b) cross-ply plates subjected to different boundary conditions and compared with the ones available in the literature.
The comparisons with the results given by and cited in these references are given in Table 1. In Table 1, the non-dimensional fundamental frequency of simply supported square plate (0/90/90/0) for a/h = 10 has been presented and compared the results from available literature. The comparisons show good agreement with most of the differences being less than 2.5%. The present results agree very nicely with the results reported earlier, particularly with those given by Xiang [11] and Reddy [19]. Figure 2 shows the non-dimensional fundamental frequency of simply supported laminated plate of various modulus ratio of E1/E2 for side-to-thickness ratio of a/h =5. It is found that the results are in very close agreement with the results of Liew [12] based on FSDT.
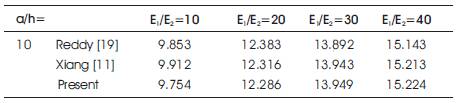
Table 1. Non-dimensional fundamental frequency of simply supported square plate (0/90/90/0)
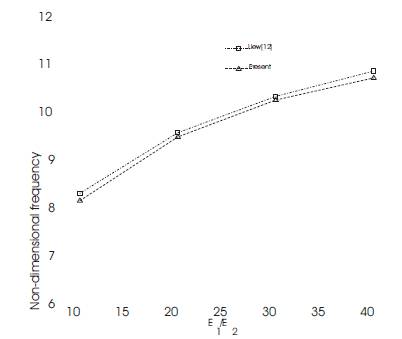
Figure 2. Non-dimensional fundamental frequency of simply supported square plate (0/90/90/0) when a/h=5
Four-layer cross-ply (0/90/90/0) laminates with a/h = 10, 20, 30, 40 are analysed to study the effect of material anisotropy. An increase of E1/E2 ratio, keeping E2 the same, leads to an increase in the fundamental frequency in the case of cross-ply laminates in thin and thick plate range and the results are shown in Figure 3. This is due to the increase in stiffness with increase in E1. It is observed that the rate of increase is more in the case of thin plates.

Figure 3. Variation of fundamental frequency with material anisotropy
The variation of non-dimensional fundamental frequency with a/h ratio for different (clamped and simply supported) edge conditions is shown in Figure 4 by analyzing the four-layer symmetric cross ply (0/90/90/0) laminates. In the case of simply-supported laminates, there is a sudden increase in the non-dimensional fundamental frequency, after that frequency remains practically constant. But, for laminates with clamped edges, the value goes on increasing with a/h ratio.
Four-layer symmetric (α/- α /- α / α) and anti-symmetric (α /- α / α /- α) laminates with the angle of fibre orientation varying from 0o to 45o with a/h = 10 and 100 are analysed. A change in fibre orientation angle from 0o to 45o leads to an increase in the fundamental frequency of vibration in the case of both thick (b/h = 10) and thin (b/h = 100) plates as shown in Figure 5. It can also be seen that the fundamental frequency of vibration for symmetric arrangement is less than that for antisymmetric arrangement, the difference being more for higher values of α.
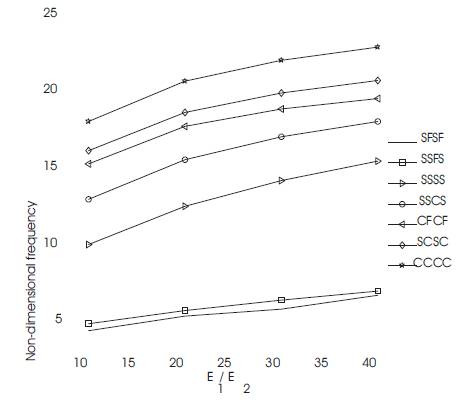
Figure 4. Variation of fundamental frequency with different boundary conditions for square plate (0/90/90/0) and a/h=10
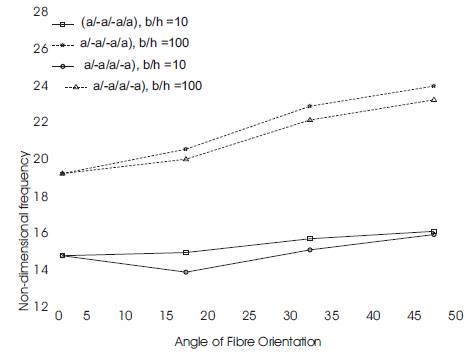
Figure 5. Variation of fundamental frequency with Fibre Orientation
The effect of aspect ratio on the fundamental frequency of vibration is studied by analyzing four-layer cross-ply (0/90/90/0) laminates with b/h = 10,50 and 100 by varying a/b ratio, keeping the value of 'b' constant in all cases. In the case of both thin and thick laminates, the fundamental frequency is found to decrease gradually with increase in aspect ratio and the variation is shown in Figure 6. This decrease is due to the decrease in stiffness of the plate with increasing aspect ratio.
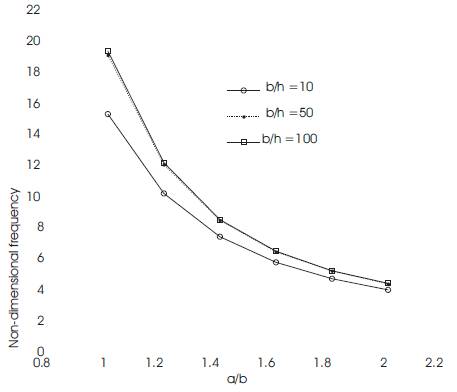
Figure 6. Variation of fundamental frequency with aspect ratio
This study dealt with the vibration analysis of laminated plates subjected to different sets of boundary conditions on the basis of a first order shear deformable plate theory. The non-dimensional fundamental frequency of vibration is found to increase with increase in width-to-thickness ratio, material anisotropy and angle of fibre orientation. The edge conditions of the plate play an important role in the frequency of vibration of the system. The fundamental frequency of vibration decreases gradually with aspect ratio. The frequency ratio increases with increase in width-to-thickness ratio.