Innumerable philosophers have expressed their opinion that mathematics is beautiful. Mathematics revel the beauty of the construction of nature, including a sapling emerging from a seed, flow of a stream, the orderliness and chaos happening in the universe, and there is no end to this list. The complexity of the movement of the planets in the solar system is explained by the simple equation of gravitation discovered by Sir Isaac Newton. Even before the Law of Gravitation was formulated, nature did not care what we thought about gravity. Several years after the law was devised, we are able to send artificial satellites around earth or passing through the edge of the solar system to probe nature or to send geostationary satellites to improve communication system, and nobody would have guessed the future implications of the law on its formulation. The universe has infinite unsolved mysteries and they will always remain to be infinite. Mathematicians can enumerate problems that has no solutions yet and this list would grow over time, and similarly mathematicians would find procedures to solve problems that were identified as unsolved problems. The Clay Mathematics Institute of Cambridge, Massachusetts, identified 7 problems (Yang–Mills and Mass Gap, Riemann Hypothesis, P vs NP Problem, Navier–Stokes Equation, Hodge Conjecture, Poincaré Conjecture and Birch and Swinnerton-Dyer Conjecture) and announced them as Prize Problems under some terms and conditions without any time frame. And, some of the problems are more than a century old. What is needed to solve these problems is creative thinking.

There are, in fact, a number of "highly lucrative" math problems. The Clay Mathematics Institute (USA) has compiled a list of Millennium Prize Problems and is prepared to pay a million dollars for the solution of each of them. The bonus of worldwide fame is also guaranteed. What are these problems? Obviously, they are incredibly hard to crack — non-specialists can have difficulty even understanding the conditions. For example, the Riemann hypothesis says:

       All the non-trivial zeros of the Reimann zeta functions ξ(s) have real part Re(s)=½

In fact, even if you do understand the formulation and manage to prove the hypothesis, its real-life application will not be easy to find. Therefore, we propose to try and solve a problem which can be easily understood and the solution of which could be of great practical importance.

We are talking about the so-called P=NP problem (It reads “p equals n-p). The problem is formulated as follows:

       Is P equal to NP ?

For a start, let’s find out what P and NP are.

The number of problems solved by computers keeps growing, and thus increases the number of calculations and the need to perform exhaustive searches. However, there are calculations that even the most powerful machines can’t cope with. For example, determining, “if a given X is a prime number.”

For relatively small numbers, there is a simple algorithm based on the enumeration of possibilities. Let’s say we need to determine whether 173 is a prime number. To do this, we need to iterate over all primes to determine whether they are divisors of 173-2 is not, 3 is not, 5 is not, and so on. You can go this way right up to 173, or you could figure out that if there are no divisors up to 13, then there would be none further along, because if you suddenly found a divisor k of the number 173, which is greater than 13, then the number n=(173÷k) would also be a divider of 173. But we assumed that k >13, which means n<173÷13<14, and we haven’t found any divisors up to 13 inclusively! That’s an apparent contradiction (Figure 1). Figure 2 shows the flowchart for finding prime numbers.

Figure 1. Finding a Prime Number using existing Prime Numbers

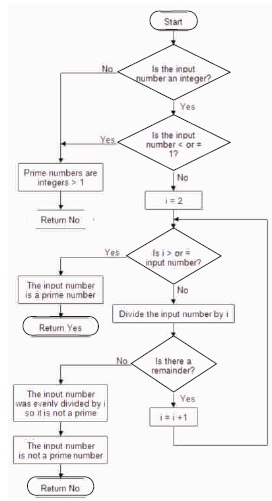
Figure 2. Flowchart for Finding Prime Numbers

Thus, the task of finding a divisor is not so difficult when the number is small. But what if it consists, for instance, of a thousand figures? Then you have to go through a huge number of possibilities. And even checking whether a given thousand-digit number divides by another significant number would be a problem of its own. Looking ahead, we should note that finding a divisor of really large numbers is a problem for all existing computers at the moment, and almost all modern cryptography is based on this fact. However, computers are capable of solving some problems and do it quite quickly. Which ones?

There is a term in the theory of algorithms — polynomial time. For example, to add two n-digit numbers, you need to make n 2 additions, and to multiply two n-valued numbers, you need to do n multiplications. Remember how you do multiplication by stacking: the first digit of n digits is multiplied by the last digit of the second number (requires n multiplications), then by the 2 second, etc. There will be n + n +...+ n (n items) multiplications, that is n operations. Then the numbers need to be added up, which is a few more n additions, but anyhow we get a polynomial depending on n number. It means that addition and multiplication problems are polynomial, or, as mathematicians say, belonging to the P class (polynomial). In other words, this is a class of problems that are solved relatively quickly and do not become much more complex with an increasing amount of data, for example, of digits in numbers.

On the other hand, there are problems that are not so easy to solve. For example, the problem of determining if a given number is a prime (search for divisors) that we discussed above. No polynomial algorithm has been found so far to solve it. In this case, the divisor can simply be tried and verified, while the division of even very large numbers itself is a polynomial task. So we have the following situation, we cannot find a divisor in polynomial time (at least, for now), but if we are lucky, we will have enough time to check whether a particular solution is correct. This is the NP (non-deterministic polynomial) problem.

Travelling salesman problem (Figure 3) is another NP Problem. Suppose there are several cities connected by air flights. The travelling salesman must visit each city once spending as little as possible on plane tickets — for example, less than the specified amount. You need to find the optimal route.

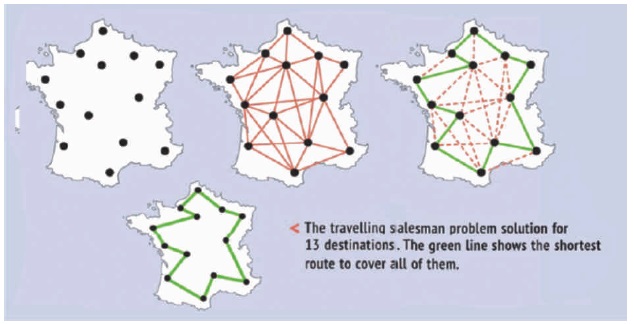
Figure 3. Simple Travelling Salesman Problem

It is an extremely complex problem to solve if the number of destinations is large enough. Indeed, if there are 1,000 of them, the travelling salesman starting in a certain city has 999 options for where to go next, then 998 cities to visit, etc. As you understand, the result is 999! options (a factorial, that is, the product of all natural numbers from 1 to 999). At the same time, any particular route is easily checked: we simply add up the amount for each flight and compare it at the end with the desired one. In general, if we are lucky, the travelling salesman problem can be solved in polynomial time, but if not — alas. So far, as we have said, a polynomial algorithm has not been invented. So this is an NP-class problem.

We have so far found out that there are P-class problems that are solved in polynomial time, and there are NP-class problems the solutions to which can be verified in polynomial time. So, as they say in the famous TV show, here's a million dollar question: are these classes of problems actually the same problem? Is it true that P = NP ?

3.1 The Essence of the Problem

There may be more than two answers to this question. In a recent survey with a hundred scientists, 61 people said that they were “not the same,” 9—that they were “equal”; 8 considered that the hypothesis was not deduced from the current axiomatic system and therefore couldn't be proved or disproved; 22 found it difficult to answer.

What is this problem about and how can one prove that these classes are equal or not equal? First, note that the NP class contains the entirety of the P class. Indeed, if the entire task is carried out in' polynomial time, then the verification of a specific solution does not go beyond that time. But the reverse problem... Is it true that any problem with a solution verified in polynomial time has a relatively quick, "polynomial" solution? After all, if we cannot come up with a quick solution to find a divisor, it does not follow from this that there is no such solution! But if someone ever proves that the task of finding the divisor can't be solved in polynomial time, we will know that NP is not equal to P, since this problem belongs to the former class and does not belong to the latter.

Well, we have figured out what the problem is. Now we need to understand why it is so important. As you remember, almost all modern cryptography is built on NP-algorithms.

It is not possible to crack such codes, because decoding problems do not have quick solutions. But if someone proves that P=NP, all information systems (for example, banking software) will be threatened, because it will mean that there is a fast, olyaomial decoding algorithm.

A mathematical problem is not an obstetrical to explore the laws of nature, in fact, they are the invitation to discover newer frontiers of knowledge. A creative thinker can discover or invent new problems and also provide models for solutions, some simple and some are complex. Variations of the statement “There is a solution to every problem,” might have been attributed to Mark Twain or H. L. Mencken or Peter Drucker or it could be even anonymous, but it might be true, that for every mathematical problem identified, there must exist at least one solution, with a possibility for improvement. For some people, the prize money could be a motivation to solve a problem, ultimately the solution would reveal the beauty in mathematics and the greatest satisfaction that money could never give. Remember, the Prize Problem list is simple and limited, and unsolved problems, as mentioned in the beginning will be infinite.